Дата регистрации 05 Декабрь 2024
245 ПродажEgri chiziqli integralning integallash yo'liga bog'liq bo'lmaslik shartlari

![bunda τi miqdor t ning t
i-1 va t
i qiymatlari orasidagi biror qiymati. xi,yi nuqtani ∆si
yoyda ixtiyoriy ravishda tanlab olish mumkin bo’lgandan, uni shunday tanlab olish
mumkinki, uning koordinatalari
τi parametrning:
xi=φ(τi)yi= ψ(τi)
qiymatlarga mos kelsin.
xi,yi va ∆xi ningtopilgan qiymatlarni (3) formulaga
qo’ysak:
∫(M)
(N)
X (x,y)dx = lim∆ti→0∑i=1
n
X [φ(τi),ψ(τi)]φ'(τi)∆ti.
O’ng tamondagi ifoda [
α,β ] kesmada olingan bitta o’zgaruvchining
X
[ φ ( τ
i ) , ψ ( τ
i )] φ ' ( τ
i ) uzluksiz funksiyasi integral yig’indisining limitidir.
Demak , bu limit shu funksiyaning aniq integraligateng:
∫
( M )( N )
X
( x , y ) dx =
∫
( α )( β )
X [ φ ( t) , ψ ( t)] φ ' ( t) dt
Xuddi shuningdek,
∫(M)
(N)
Y(x,y)dx =∫(α)
(β)
Y[φ(t),ψ(t)]ψ'(t)dt
formula hosil qilinadi. Bu tengliklarni hadlab qo’shsak:
∫
(
M)
( N)
X
( x , y ) dx + Y ( x , y ) dy =
∫
(
α)
(β)
X
[ φ ( t) , ψ ( t)] φ ' ( t) dt + ¿
+ Y
[ φ ( t) , ψ ( t)] ψ ' ( t) dt ( 1.2 .4 )
Bu esa egri chiziqli integralni hisoblash uchun izlangan formulaning o’zi dir.
x=φ(t),y= ψ(t),z= χ(t)
tenglamalar bilan berilgan fazoviy egri chiziq bo’yicha
∫ Xdx +Ydy +Zdz
egri chiziqli integral ham shuning singari hisoblanadi.
13](https://docx.uz/documents/b16747f8-14aa-48eb-bef6-ffddda1db941/page_12.png?v=3)
![nuqtalarni bildirganligi uchun ular qavs ichiga olib yozilgan. L egri chiziq bo’yicha
M nuqtadan N nuqtaga qarab olingan yo’nalish integrallash yo’nalishi deb ataladi.
Agar L fazoviy egri chiziq bo’lsa,u holda uchta X(x,y,z),Y(x,y,z) va Z(x,y,z)
funksiyaning egri chiziqli integrali yuqoridagi singari aniqlanadi.∫L
❑
X (x,y,z)dx +¿Y(x,y,z)dy +Z(x,y,z)dz =¿¿
¿ lim
∆ x
k → 0
∆ y
k → 0
∆ z
k → 0 ∑
i = 1n
[
X ( x
k , y
k , z
k ) ∆ x
k + Y ( x
k , y
k , z
k ) ∆ y
k + Z ( x
k , y
k , z
k ) ∆ z
k ]
Integral belgisi ostida turgan L harfi integrallashni L egri chiziq bo’yicha bajarish
kerakligini ko’rsatadi.
Egri chiziqli integralning ikkita xossasini ko’rib chiqamiz.
1.1.2-rasm
1-xossa. Egri chiziqli ostidagi ifoda integral egri chizig’ining shakliga va
ko’rsatilgan integral yo’nalishi bilan aniqlanadi.
Integrallashning yo’nalishi o’zgarishi bilan egri chiziqli integralning ishorasi
ham o’zgaradi, chunki bunda ∆ s
vektorning ishorasi demak, uning ∆ x
va ∆ y
proeksiyalarining ishoralari ham o’zgaradi.
2-xossa. L egri chiziqni K nuqta
˘MN = ˘MK + ˘KN bo’ladigan qilib, L
1 va L
2
bo’laklarga bo’lamiz(1.1.2-rasm). Bu holda (1) formuladan bevosita
9](https://docx.uz/documents/b16747f8-14aa-48eb-bef6-ffddda1db941/page_8.png?v=3)

![egri chiziqli integrali funksiyaning shu nuqtadagi qiymatlarining∫(M)
(N)
Xdx +Ydy = ∫(M)
(N)
du (x,y)= u(N )− u(M )
ayirmaga tengligini isbot qilamiz.
Isbot. Agar Xdx + Ydy
ifoda
u(x,y) funksiyaning to’liq differensiali bo’lsa, u
holda X = ∂ u
∂ x ; Y = ∂ u
∂ y va egri chiziqli integral quydagi shakilda bo’ladi:
I= ∫(M)
(N)∂u
∂xdx +∂u
∂ydy .
Bu integralni hisoblash uchun M va N nuqtalarni tutashtiruvchi L egri
chiziqning parametric tenglamasini yozamiz:
x=φ(t),y= ψ(t).
Parametrning
t=t0 qiymatiga M nuqta, t=T qiymatiga esa N nuqta mos keladi
deb hisoblaymiz. Bu holda egri chiziqli integral quydagi aniq integralga keltiriladi:
I =
∫
t
0T
[ ¿ ∂ u
∂ x ∂ x
∂ t + ∂ u
∂ y ∂ y
∂ t ] dt . ¿
Qavs ichidagi ifoda u [ φ
( t) , ψ ( t) ]
funksiyadan t bo’yicha olingan to’liq hosila bo’lib,
t ning funksiyasidir . shuning uchun
I =
∫
t
0T
∂ u
∂ t dt = u
[ φ ( t) , ψ ( t)] T
¿
t
0 = u [ φ ( t) , ψ ( t)] − u [ φ ( t
0 ) , ψ ( t
0 )] = ¿
¿ u
( N ) − u ( M ) .
To’liq diffirensialning egri chiziqli integrali integral olinadigan egri
chiziqning shakliga bog’liq emasligini ko’ramiz.
Bunga o’xshash muhokama fazoviy egri chiziq bo’yicha olingan egri chiziqli
integral uchun ham o’rinlidir.
31](https://docx.uz/documents/b16747f8-14aa-48eb-bef6-ffddda1db941/page_30.png?v=3)
![1.4-§. Grin formulasi
Biror D tekis soha bo’yicha olingan ikki o’lchovli integral bilan shu
sohaning L chegarasi bo’yicha olingan egri chiziqli integral orasidagi munosabatni
aniqlaymiz.
Oxy tekislikda L yopiq kontur bilan chegaralangan Ox o’q yo’nalishida
ham, Oy o’q yo’nalishida ham to’g’ri bo’lgan D yopiq soha berilgan bo’lsin. Bu
soha pastdan y=y
1 (x) egri chiziq bilan yuqoridan esa y= y
2 (x) egri chiziq bilan
chegaralangan va y1(x)≤ y2(x) ( a ≤ x ≤ b
) bo’lsin (1.3.6-rasm).
Bu ikkala egri chiziq birgalikda L yopiq konturni tashkil etadi. D soha
uzluksiz xususiy hosilalarga ega bo’lgan X(x,y) va Y(x,y) uzluksiz funksiyalar
berilgan bo’lsin.
Endi ushbu
∬
D❑
∂ X
( x , y )
∂ y dxdy
integralni qarab chiqamiz. Uni ikki karrali integral shaklida tasvirlab quydagini
hosil qilamiz:
∬D
❑ ∂X
∂y dxdy =∫a
b
¿¿
¿
∫
ab
[ X ( x , y
2
( x ) )
¿ − X ( x , y
1 ( x ) ) ] dx . ( 1.4 .1 ) ¿
∫a
b
X (x,y2(x))dx
integral son jihatdan tenglamasi parametric shaklda x=x, y=
y2(x) bo’lgan (x-
parametr) MPN egri chiziqli integralga teng ekanligini ko’rsata miz. Shunday qilib,
∫
ab
X ( x , y
2
( x ) ) dx =
∫
( MPN )❑
X ( x , y ) dx . ( 1.4 .2 )
21](https://docx.uz/documents/b16747f8-14aa-48eb-bef6-ffddda1db941/page_20.png?v=3)












![bo’lsin, bundagi X(x,y) va Y(x,y) lar F vektorning OX va OY o’qlardagi
proeksiyalari, x
i va y
i koordinatalarning M
i nuqtadan M
i+1 nuqtaga o’tishdagi
ortirmalarini ∆xi va ∆ yi bilan belgilab, quydagini hosil qilamiz:
∆si= ∆xi
i + ∆ yi j .
Demak,
Fi
∆si= X (xi,yi)∆xi+Y(xi,yi)∆yi .
F kuchning butun MN egri chiziq bo’yicha bajargan A ishning taqribiy qiymati
quydagicha bo’ladi:
A≈∑i=1
n
Fi∆si=∑i=1
n
[X (xi,yi)∆xi+Y(xi,yi)∆yi].(1.1 .1)
Hozircha aniq ta’rifni bermasdan agar ∆ s
i → 0
da tenglikning o’ng
tamonidagi ifodaning limiti mavjud bo’lsa (bunda
∆xi→ 0 va ∆ yi→ 0 ekanligi
ravshan), bu limit F kuchning L egri chiziq bo’yicha M nuqtadan N nuqtagacha
bajargan ishini ifodalaydi:
A= lim∆xi→0 ∆yi→0
∑i=1
n
[X (xi,yi)∆xi+Y(xi,yi)∆ yi],(1.1 .2)
O’ng tamondagi limit X(x,y) va Y(x,y) funksiyalarning L egri chiziq bo’yicha
olingan egri chiziqli integrali deb ataladi va quydagicha belgilanadi:
A =
∫
L❑
X
( x , y ) dx + Y ( x , y ) dy ( 1.1 .3 )
yoki
A= ∫(M)
(N)
X (x,y)dx +Y(x,y)dy (1.1 .3')
(2) ko’rinishidagi yig’indining limitlari ko’pincha matematika va mexanikada
uchrab turadi, bunda X(x,y) va Y(x,y) ikkita o’zgaruvchining biror D sohadagi
funksiyalari deb qaraladi.
Integrallash chegaralari o’ziga qo’yilganM va N harflari sonini emas, balki
egri chiziqli integral olinishi kerak bo’lgan chiziqning boshlang’ich va oxirgi
8](https://docx.uz/documents/b16747f8-14aa-48eb-bef6-ffddda1db941/page_7.png?v=3)



![Izoh. Bazan ixtiyoriy X ( x , y )
funksiyaning L yoy uzunligi bo’yicha
olingan egri chiziqli:
∫
L❑
X( x , y ) ds = lim
∆ S
i → 0 ∑
i = 1n
X ( x
i , y
i ) ∆ S
i ( 1.4 .15 )
integralni qarashga to’g’ri keladi, bunda
ds yoy differensiali. Bunday integrallar
ham yuqorida qaralgan egri chiziqli integralni hisoblash kabi hisoblanadi. L egri
chiziq o’zining
x=φ(t),y= ψ(t)
parametric tenglamalari bilan berilgan bo’lsin, bu yerda
φ(t),ψ(t),φ'(t),
ψ '
( t)
lar t ning uzluksiz funksiyalari.
t
parametrning α
va β
qiymatlari L yoyning boshlang’ich va oxirgi uchlariga
mos kelsin.
ds =
√ φ '
( t ) 2
+ ψ ' ( t) 2
dt
ekanligini hisobga olsak, (1.4.15) integralni hisoblash uchun ushbu formulani hosil
qilamiz:
∫
L❑
X
( x , y ) ds =
∫
αβ
X [ ¿ ¿ φ ( t) , ψ ( t ) ] √ φ ' (
t) 2
+ ψ ' ( t) 2
dt . ¿ ¿
x = φ
( t) , y = ψ ( t) , z = χ ( t )
fazoviy egri chiziq yoyi bo’yicha olingan egri chiziqli
integralni ham qarash mumkin:
∫L
❑
X (x,y,z)ds =∫α
β
X [¿¿φ(t),ψ(t),χ(t)]√φ'(t)2+ψ'(t)2+χ'(t)2dt .¿¿
Yoy bo’yicha olingan egri chiziqli integrallar yordami bilan, masalan, chiziqlar
og’irlik markazining koordinatalari aniqlanadi.
32](https://docx.uz/documents/b16747f8-14aa-48eb-bef6-ffddda1db941/page_31.png?v=3)
![y = y
2( x ) ,
[y¿¿1(x)≤ y2(x)]¿
(
l2 ) egri chiziq bilan chegaralanadi, deb faraz qilamiz. U holda D sohaning yuzi:
S =
∫
ab
y
2
( x ) dx −
∫
ab
y
1 ( x ) dx .
Biroq y = y
2
( x )
tenglama l
2 ( ˘
MPN )
egri chiziqning tenglamasi bo’lgandan,
birinchi integral shu egri chiziq bo’yicha olingan egri chiziq bo’yicha olingan egri
chiziqli integraldir; demak,
∫a
b
y2(x)dx = ∫MPN
❑
ydx .
Ikkinchi integral esa l
1 ( ˘
MQN )
egri chiziq bo’yicha olingan egri chiziqli integral,
ya’ni:
∫a
b
y1(x)dx = ∫MQN
❑
ydx .
Egri chiziqli integralning 1- xossasiga asosan:
∫
MPN ❑
ydx = −
∫
NPM ❑
ydx .
Demak,
S = −
∫
NPM ❑
ydx −
∫
MQN ❑
ydx = −
∫
L❑
ydx . ( 1.3 .5 )
Bu holda L egri chiziq soat strelkasi yo’nalishiga teskari yo’nalishda aylanib
chiqiladi.
17](https://docx.uz/documents/b16747f8-14aa-48eb-bef6-ffddda1db941/page_16.png?v=3)



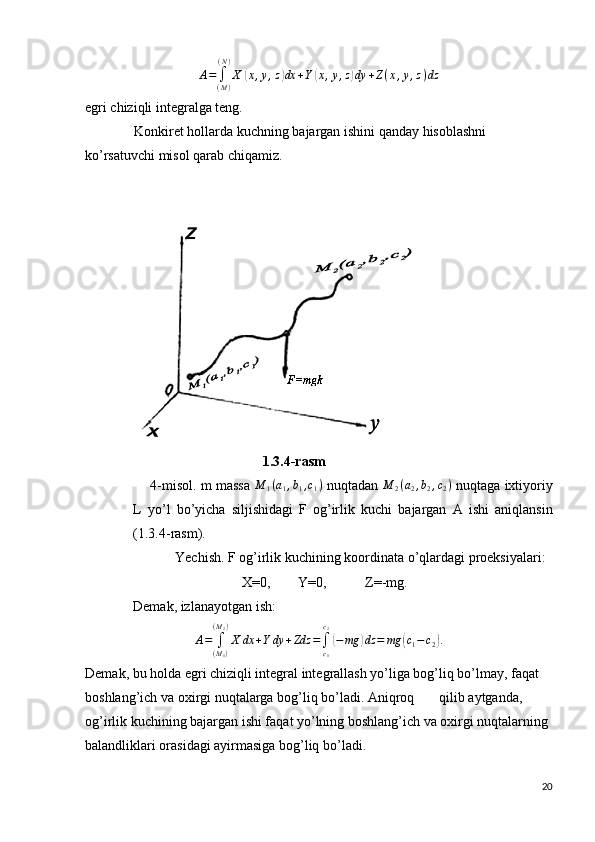




![Demak,
∫
( M )( N )
6 x 2
ydx + 10 x y 2
dy =
∫
12
( 6 x 2
¿
x 3
∙ 1 + 10 x yx 6
∙ 3 x 2
) dx = ¿ ¿¿∫1
2
(6x5¿+30 x9)dx =¿¿
1.3-§. Egri chiziq bilan chegaralangan sohaning yuzi egri chiziqli integral
orqali ifodalash.
1.3.1-rasm
Oxy tekislikda L kontur bilan chegaralangan shunday D soha berilgan bo’lsinki, bu
sohaning ichki nuqtasi orqali koordinata o’laridan birortasiga parallel holda
o’tuvchi ixtiyoriy to’g’ri chiziq sohaning L chegarasini ko’p deganda ikki nuqtada
kessin (ya’ni D to’g’ri soha bo’lsin) (1.3.1-rasm).
D soha Ox o’qidagi [a, b] kesma proeksiyalanadi, bunda soha pastdan
y = y
1 ( x )
(
l1 ) egri chiziq bilan chegaralanadi, yuqoridan esa
16](https://docx.uz/documents/b16747f8-14aa-48eb-bef6-ffddda1db941/page_15.png?v=3)
![1-misol. Quydagi uchta x 3
, 3zy 2
, -x 2
y funksiyaning (yoki barbir
x 3
i+ 3zy 2
j -x 2
y k vektor funksiyaning) egri chiziqli integrali M(3,2,1) nuqtadan
chiqib, N(0,0,0) nuqtaga tamon yo’naltiruvchi to’g’ri chiziq kesmasi bo’yicha
hisoblansin(1.2.2-rasm). 1.2. 2-rasm
Yechim. Integrallash kerak bo’lgan MN chiziqning parametric
tenglamasini toppish uchun berilgan ikki nuqtadan o’tuvchi to’g’ri chizqning
x
3 = y
2 = z
1
tennglamasini yozib, bu nisbatlarning hammasini bitta t harfi bilan belgilaymiz va
to’g’ri chiziqning
x = 3 t , y = 2 t , z = t
ko’rinishidagi parametric tenglamasini hosil qilamiz. Bunda MN kesmaning bosh
uchiga esa parametrning t=1 qiymati, oxirgi uchiga esa parametrning t=0 qiymati
mos keladi. x, y, z dan t parameter bo’yicha olingan (egri chiziqli integralni
hisoblashda kerak bo’ladigan ) hosilalar osongina topiladi:
x '
t = 3 , y '
t = 2 , z '
t = 1
Endi izlanayotgan egri chiziqli integralni (4) formula yordami bilan
hisoblash mumkin:
∫
( M )( N )
x 3
dx + 3 z y 2
dy − x 2
ydz =
∫
10
[ ( 3 t ) 3
¿
∙ 3 + 3 t ( 2 t ) 2
∙ 2 − ( 3 t ) 2
2 t ∙ 1 ] dt = ¿ ¿¿∫1
0
87 t3dt = −87
4 .
14](https://docx.uz/documents/b16747f8-14aa-48eb-bef6-ffddda1db941/page_13.png?v=3)

![∫
L❑
X( x , y ) dx + Y ( x , y ) dy ( 1.2 .1 )
egri chiziqli integralni qaraymiz. Egri chiziqli integralning mavjudligi haqidagi
teoremani isbotisiz keltiramiz.
Teorema. Agar φ
( t)
va ψ ( t)
funksiyalar uzluksiz va
φ ' ( t)
, ψ ' ( t)
uzluksiz
hosilalarga ega, shuningdek X[
φ(t) , ψ ( t)
] va Y[ φ(t) , ψ ( t)
] funksiyalar t argumentning
funksiyasi sifatida [
α,β ] kesmada uzluksiz bo’lsa, u holda
lim
∆ x
i → 0 ∑
i = 1n
X
( x
i , y
i ) ∆ x
i = A
lim
∆ y
i → 0 ∑
i = 1n
Y
( x
i , y
i ) ∆ y
i = B } ( 1.2 .2 )
limitlari mavjud bo’ladi. Bunda, x
i va y
i lar ∆ s
i yoyda yotuvchi biror nuqtaning
koordinatalari. Bu limitlar
∆si→ o da L yoyni ∆si yoychalarga bo’lish usuliga va
∆ s
i yoyda M
i
( x
i , y
i ) nuqtaning tanlab olinishiga bog’liq emas; ular egri chiziqli
integrallar deb ataladi va bunday belgilanadi:
A =
∫
L❑
X
( x , y ) dx , A =
∫
L❑
X ( x , y ) dx ( 1.2 .2 ' )
Izoh. Teoremadan oldingi panagrifda aniqlangan yig’indini ham o’sha
limitga, ya’ni egri chiziqli integralga intilishi kelib chiqadi, bunda M
i
( x
i , y
i )
nuqtalar
∆si yoyning oxirgi uchlari, L yoyni ∆si bo’laklarga bo’lish sistemasi esa
ixtiyoriydir.
Ifodalangan teorema egri chiziqli integralni hisoblash usulini hosil qilishga imkon
beradi.
Demak, ta’rifga asosan:
∫
( M )( N )
X
( x , y ) dx = lim
∆ x
i → 0 ∑
i = 1n
X ( x
i , y
i ) ∆ x
i , ( 1.2 .3 )
bunda
∆xi= xi− xi−1= φ(ti)−φ(ti−1).
So’ngi ayirmani Lagranj formulasi bo’yicha almashtiramiz:
∆ x
i = φ
( t
i ) − φ ( t
i − 1 ) = φ ' (
τ
i )( t
i − t
i − 1 ) ,
12](https://docx.uz/documents/b16747f8-14aa-48eb-bef6-ffddda1db941/page_11.png?v=3)
Egri chiziqli integralning integallash yo'liga bog'liq bo'lmaslik shartlari
Kirish
1.1.Egri chiziqli integral
1.2. Egri chiziqli integralni hisoblash
1.3. Egri chiziq bilan chegaralangan sohaning yuzi egri chiziqli integral orqali ifodalash
1.4. Grin formulasi
Xulosa
Adabiyotlar ro’yxati