• Всего документов: 5844
  • Число пользователей: 15251

Информация о документе

Цена 12000UZS
Размер 458.1KB
Покупки 0
Дата загрузки 19 Декабрь 2024
Расширение docx
Категория Алгебра

Продавец

Bahrom

Дата регистрации 05 Декабрь 2024

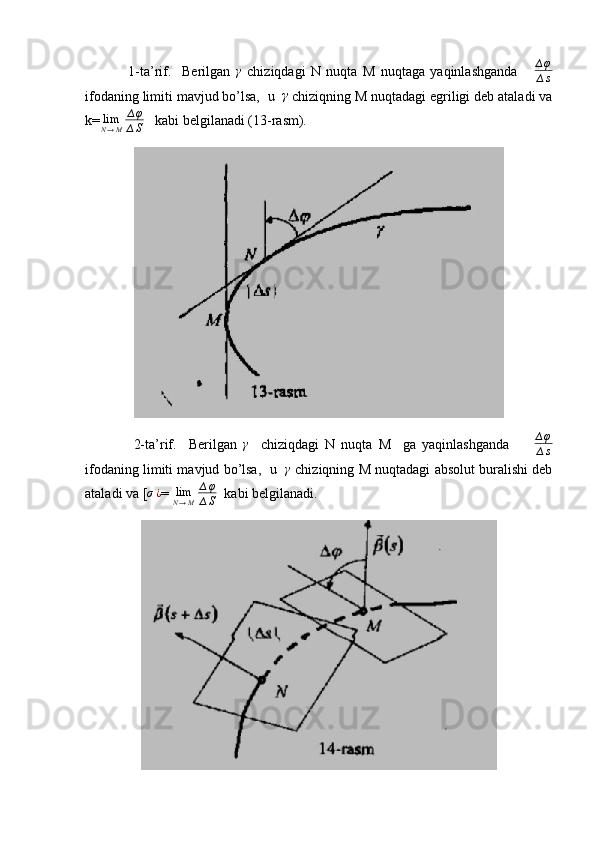
245 Продаж

Egri chiziqning egriligi va buralishi

1-ta’rif. Fazodagi (yoki tekislikdagi) γ to’plam birorta ochiq intervalning topologik (gomeomorf) akslantirishdagi aksi bo’lsa, ya’ni birorta f : (a, b) → R 3 akslantirish uchun f((a, b))= γ tenglik o’rinli bo’lib, f : (a, b) → γ topologic akslantirish bo’lsa, γ elementar chiziq deb ataladi. Bu ta’rifga ko’ra, ochiq (a, b) intervalga tegishli ixtiyoriy t nuqtaga mos keluvchi nuqtani γ(t) bilan belgilasak, u holda { x= x(t) y= y(t) z= z(t) a ¿t<b (1) tenglamalar γ chiziqning parametric tenglamalari deyiladi. Differensial geometriya kursida egri chiziq parametric tenglamalar yordamida o’rganiladi, ya’ni γ chiziqni aniqlovchi f akslantirish tanlanib , uning parametric tenglamalari yoziladi, bu holda γ chiziqni parametrlangan elementar chiziq deb ataymiz. 2-ta’rif. Berilgan γ elementar egri chiziqni differensiallanuvchi x(t), y(t), z(t) funksiyalar yordamida parametrlash mumkin bo’lsa, u silliq elementar egri chiziq deb ataladi. Izoh: Zarur bo’lgan hollarda, biz yuqori tartibli hosilalarning mavjud va uzluksiz bo’lishini talab qilamiz. 3-ta’rif: Bog’lanishli γ to’plamga tegishli har qanday M nuqtaning har qanday U M atrofi mavjud bo’lib, γ to’plamning U M atrofidagi qismi elementar egri chiziq bo’lsa, γ sodda egri chiziq deb ataladi. 1-tasdiq. Har qanday sodda egri chiziq yoki elementar egri chiziqdir yoki aylanaga gomeomorfdir. 4-ta’rif. Bizga sodda elementar γ egri chiziq berilgan bo’lib, M esa unga tegishli nuqta bo’lsin. Agar U M to’plam M nuqtaning atrofi bo’lsa, U M ∩ γ kesishmani M nuqtaning γ chiziqdagi atrofi deb ataladi. 5-ta’rif. Sodda egri chiziqning local topologic akslantirishdagi obrazi umumiy egri chiziq deyiladi. 2-tasdiq. Silliq x(t), y(t), z(t) funksiyalar hosilalari har bir t ϵ(a,b) uchun x’ 2 (t)+y’ 2 (t)+z’ 2 (t) ¿0 shartni qanoatlantirsa, (1) tenglamalar sistemasi umumiy egri chiziqni ifodalaydi. Bu umumiy egri chiziq (a,b) intervalning f: t → (x(t),y(t),z(t)) akslantirishdagi aksidir. 2-masala. Parabola y=x 2 -6x+15 funksiyaning grafigidan iborat bo’lsa, uning qaysi nuqtalaridagi urinmalari x-2y+18=0 to’g’ri chiziqqqa perpendicular bo’ladi. Yechish. Parabolaning M (x 0 ,y 0 ) nuqtasida o’tkazilgan urinma tenglamasi ushbu x − x 1 =y− y 2x−6 ko’rinishda bo’ladi. Bu tenglamadan 2(x 0 -3)-y-2(x 0 - 3)+y 0 =0 tenglikni, to’g’ri chiziqlarning perpendicular ekanligidan esa 1·2(x 0 -3)- 2(-1)=0 shartni hosil qilamiz. Bundan x 0 =2 qiymatni topamiz. Endi izlanayotgan nuqtaning ordinatasini aniqlaymiz: y 0 =2 2 +6·2+15=7. Demak, (2,7) nuqtada o’tkazilgan urinma berilgan to’g’ri chiziqqa perpendicular bo’lar ekan. Haqiqatan ham bu nuqtada o’tkazilgan urinma tenglamasi 2x+y-11=0 ko’rinishida bo’lib, u berilgan x-2y+18=0 to’g’ri chiziqqa perpendicular bo’ladi (5-rasm). 3-tasdiq. Bizga differensiallanuvchi φ (x,y) funksiya berilgan bo’lib, koordinatalari φ (x,y)=0 tenglamani qanoatlantiruvchi nuqtalar to’plamini M={(x,y): φ (x,y)=0 } deb belgilaylik. Agar (x 0 ,y 0 ) Mϵ nuqtada φ+φ y 2 ¿0 munosabat bajarilsa, (x 0 ,y 0 ) nuqtqaning shunday atrofi mavjudki, M to’plamning bu atrofdagi qismi elementar egri chiziq bo’ladi. 4-tasdiq. Silliq elementar γegri chiziqning parametric tenglamalari (1) ko’rinishda bo’lib, t 0 ∈ (a,b) uchun x’(t 0 ) ≠ 0 bo’lsa, ((x 0, y 0, z 0 ) nuqtaning kichik atrofida γ ni { y = φ ( x ) , z = τ ( x ) , a ¿x<b tenglamalar yordamida aniqlash mumkin. Bu yerda x 0 =x(t 0 ), y 0 =y(t 0 ), z 0 =z(t 0 ) 5-tasdiq. F(x, y, z) va G(x, y, z) uch o’zgaruvchili silliq fumksiyalar, M esa koordinatalari { F ( x , y , z ) = 0 G ( x , y , z ) = 0 sistemani qanoatlantiruvchi nuqtalar to’plami bo’lsin. Agar (x 0, y 0, z 0 ) Mϵ nuqtada ( F ,F ,F G ,G ,G) matritsaning rangi ikkiga teng bo’lsa , (x 0, y 0, z 0 ) nuqtaning shunday atrofi mavjudki, M ning bu atrofdagi silliq qismi silliq elementar egri chiziq bo’ladi. 6-ta’rif. Silliq γ chiziqni unga tegishli har qanday nuqtaning birorta atrofida ixtiyoriy t ϵ ( a , b ) uchun x’ 2 (t)+y’ 2 (t)+z’ 2 (t) ¿ 0 shartni qanoatlantiruvchi differensiallanuvchi x(t), y(t), z(t) funksiyalar yordamida parametrlash mumkin bo’lsa, u regulyar egri chiziq deyiladi. Masalalar yechish namunalari 1-masala. O’zgarmas a uzunlikka ega bo’lgan AB kesma o’z o’qiga perpendicular bo’lib , uning A uchi shu o’qda yotadi. Kesma A uchi aylanish burchagiga proporsional yo’lni bosib boradigan holda, o’z o’qi bo’yicha siljib , shu o’q atrofida aylanadi. Ushbu harakat natijasida kesmaning B uchi chizgan chizig’I vint chizig’i deyiladi. Vint chizig’ining tenglamasini tuzing. Tasdiq. Uch marta differensiallanuvchi regulyar γ egri chiziqning M nuqtada egriligi noldan farqli bo’lsa, [ σ¿ = lim N → M ∆ φ ∆ S limit mavjud. Agar γ egri chiziq tabiiy parameter yordamida ⃗r = ⃗r (s) tenglama bilan berilgan bo’lsa, uning absolut buralishi, [ σ¿ = [(r,r',r'')] [r]2 formula bo’yicha hisoblanadi. Buralish esa σ = ( r , r ' , r ' ' ) k 2 formula bilan, ixtiyoriy parametrlash usuli bilan berilgan egri chiziq uchun buralishni hisoblash formulasi σ =- (r',r'',r''') [r',r'']2 ko’rinishda bo’ladi. Agar egri chiziq { x= x(t) y= y(t) z= z(t) tenglama bilan berilgan bo’lsa, uning buralishini topish formulasi quyidagicha σ= − [ x' y' z' x'' y'' z'' x''' y''' z'''] | y' z' y'' z''|+| z' x' z'' x''|+| x' y' x'' y''| ko’rinishda bo’ladi. Tabiiy parametrlash usuli bilan ⃗r = ⃗r (s) tenglama yordamida berilgan egri chiziq urinma, bosh normal, binormallari bo’yicha yo’nalgan birlik vektorlar va ularning hosila vektorlari orasidagi bog’liqlikni ifodalaydigan Frene formulalari ushbu ko’rinishda bo’ladi: ko’rinishda bo’ladi. Egri chiziqning M(t 0 ) nuqtasidan o’tuvchi urinma to’g’ri chiziqqa perpendicular holda o’tuvchi to’g’ri chiziq normal deb ataladi. Normallar ichida biz uchun muhimlari bosh normal va binirmaldir. Yopishma tekislikda yotuvchi normal bosh normal deb ataladi. Yopishme tekislikka perpendicular normal esa binormal deb ataladi. Albatta yopishma tekislik yagona bo’lgan holdagina bu tushunchalar ishlatiladi. Endi bosh normal va binormal tenglamalarini yozaylik. ⃗r' (t 0 ) va ⃗r'' (t 0 ) vektorlar yopishma tekislikka parallel bo’lgani uchun vector ko’paytma ¿ (t 0 ), ⃗r'' (t 0 )] binormal uchun yo’naltiruvchi vector bo’ladi. Demak binormal tenglamasi X − x | y ' ( t ) z ' ( t ) y ' ' ( t ) z ' ' ( t ) | = ¿ Y− y | z'(t) x'(t) z''(t) x''(t)| = Z− z | x'(t) y'(t) x''(t) y''(t)| ko’rinishda bo’ladi. Bosh normal uchun esa ¿ (t 0 ), [ ⃗r'' (t 0 ), ⃗r'' (t 0 )]] vector ko’paytma yo’naltiruvchi vector bo’ladi.. shuning uchun bosh normal tenglamasi, X − x y ' ( t)| x ' ( t) y ' ( t) x ' ' ( t) y ' ' ( t)| − z ' ( t ) | z ' ( t ) x ' ( t ) z ' ' ( t ) x ' ' ( t ) | = ¿ Y − y z ' ( t)| y ' ( t) z ' ( t) y ' ' ( t) z ' ' ( t)| − x ' ( t ) | x ' ( t ) y ' ( t ) x ' ' ( t ) y ' ' ( t ) | = Z − z x ' ( t)| z ' ( t) x ' ( t) z ' ' ( t) x ' ' ( t)| − y ' ( t ) | y ' ( t) z ' ( t) y ' ' ( t) z ' ' ( t)| ko’rinishda bo’ladi. Xuddi shularga o’xshash normal tekislik tenglamasi vector ko’rinishda ( ⃗R - ⃗r (t 0 ), r ' (t 0 ))=0, koordinata ko’rinishidagi tenglamasi esa (X-x(t 0 ))x’(t 0 )+ (Y- y(t 0 ))y’(t 0 )+ (Z-z(t 0 ))z’(t 0 )=0 bo’ladi. Urinma va binormaldan o’tuvchi tekislik to’g’rilovchi tekislik deyiladi. Uning vector ko’rinishidagi tenglamasi ( ⃗R - ⃗r (t 0 ), ⃗r' (t 0 ), ¿ (t 0 )])=0 koordinata ko’rinishidagi tenglamasi esa { x= acos φ y=asin φ z=τφbo’ladi. Vint chizig’ining o’zi yasovchilari Oz o’qiga parallel bo’lgan x 2 +y 2 =a 2 silindrda yotadi. Chunki AB kesmaning uzunligi o’zgarmaydi. (1-rasm). 1.2-§. Vektor funksiyalar uchun differensial hisob Differensial geometriya va topologiya fanida vector analizi muhim o’rin tutadi. Shuning uchun bu paragrafda qisqacha vector funksiyalar xossalariga doir misol va masalalar keltiramiz. Bizga biror G to’plam berilgan bo’lsin. Agar G to’plamning har bir nuqtasiga aniq bitta vector mos qo’yilgan bo’lsa, G to’plamda vector funksiya berilgan deyiladi. Bu moslikni p → r(p) ko’rinishda yozish mumkin. 1-ta’rif. Berilgan ⃗r (p) vektor funksiya va o’zgarmas a→ uchun p → p 0 da r(p)-a → 0 munosabat bajarilsa, ⃗ r (p) vector funksiya p → p 0 da a limitga ega deyiladi va lim p → p r ( p ) =a ko’rinishda yoziladi. Tasdiq. Fazoda kiritilgan dekart koordinatalar sistemasida berilgan vektorlarning komponentalari r(p)= {(x(p), y(p), z(p)}, a→ = {a 1 , a 2 , a 3 } bo’lsa ushbu tenglik lim p → p r ( p ) =a quyidagi uchta munosabatga ekvivalentdir: lim p → p x ( p ) =a 1, limp→pr(p) =a 2, lim p → p z ( p ) =a 3 Vector funksiyalar uchun uzliksizlik va differesiallanuvchanlik tushunchalari skalar funksiyalar uzluksizligi va differensiallanuvchanligi tushunchalari kabi kiritiladi. 2-ta’rif. Ushbu lim p → p r ( p ) =r(p 0 ) munosabat bajarilsa, r(p) vector funksiya p 0 nuqtada uzluksiz deyiladi. Vector funksiya aniqlangan G to’plam sonlar o’qining qism to’plami bo’lsa, r(p) vector funksiya bir o’zgaruvchili vector funksiya deyiladi. Agar p 0 ϵ G nuqta uchun lim h → 0 r ( p + h ) − r ( p ) h Tadqiqotimizning asosiy ilmiy – uslubiy yangiligi: -egri chiziqning egriligi va buralishiga doir masalalarni o’rganish, nazariy, uslubiy izlanishlar olib borildi. -muammoni yechimlarini o’rganishni takomillashtirish bo’yicha alohida metodik ishlanma ishlab chiqildi. Kurs ishining metodlari : Tadqiqot muammosiga oid pedagogik- psixologik va metodik adabiyotlar mazmunini o’rganish, nazariy jihatdan tahlil qilish, matematikani o’qitishda zamonaviy texnologiyalarni qo’llash holatini o’rganish, pedagogik kuzatuv, suhbat, pedagogik tajriba va h.k. Kurs ishining tuzilishi: Kurs ishi kirish, 4ta asosiy qism, xulosa va foydalanilgan adabiyotlar ro’yxatidan iborat. I BOB. CHIZIQLAR NAZARIYASI. 1.1-§. Egri chiziq va uning berilish usullari 1. A.Ya. Narmanov , A. S. Sharipov “ differensial geometriya va topologiya kursidan masalalar to’plami”, Toshkent . 2014. 2. A. Xudoyberganov "Matematika", Darslik, Toshkent, "O'qituvchi"-1980 yil. 3. N.Ya.Vilenkin va boshqalar "Matematika", Moskva, "Prosvesheniya"-1977 y. 4. N.Ya.Vilenkin va boshqalar "Zadachnik praktikum po matematike", Uchebnik, Moskva, "Prosvesheniya"-1977 y. 5. P.Ibragimov "Matematikadan masalalar to'plami", O'quv qo'llanma, Toshkent, "O'qituvchi"-1995 yil. 6. P.Azimov, H.Sherboyev, Sh.Mirhamidov, A.Karimova "Matematika", O'quv qo'llanma, Toshkent, "O'qituvchi"-1992 yil. 7. J. Ikromov "Maktab matematika tili", Toshkent, "O'qituvchi"-1992 yil. 8. P.P.Stoylova, N.Ya.Vilenin "Seliye neotritsatelniye chisla", Moskva, "Prosvesheniya"-1986 y 9. A.M.Pishkalo, P.P.Stoylova "Sbornik sadach po matematike", Moskva, "Prosvesheniya"-1979 y. 10. T.Yoqubov, S.Kallibekov "Matematik mantiq elementlari", Toshkent, "O'qituvchi"-1996 yil. 11. T.Yoqubov "Matematik mantiq elementlari", Toshkent,"O'qituvchi"-1983 y. 12. С. И. Новоселов "Специальный Курс Элементарной Алгnры" 1958- йил. 13. www.ziyonet.uz 4-masala. (x-C) 3 -y 2 =0 tenglama bilan berilgan parabolalar oilasining o’ramasi topilsin. Yechish. Ravshanki, berilgan oilaning discriminant chizig’i y=0 to’g’ri chiziq bo’ladi. Vu to’g’ri chiziq nuqtalari berilgan oilaning maxsus nuqtalaridan iborta bo’lganligi uchun buchiziq oilaning o’ramasi bo’lolmaydi (10rasm). 2.2-§ Frene bazisi. Egri chiziqning parametrizatsiyasi Chiziqlar nazariyasini o’rganishda urinma muhim rol o’ynashi hammag ma’lum. Urinmaga perpendicular tekislikni normal tekislik deb ataganmiz. Bu paragrafda urinmaga perpendicular ikki vector binormal va bosh normal deb ataluvchi vektorlarning xossalari o’rganiladi. Bizga γ egri chiziq va uning M nuqtasidan o’tuvchi birorta α tekislik berilgan bo’lsin. Berilgan chiziqdagi M nuqtaga yaqin N nuqta olib M va N nuqtalar orasidagi masofani d bilan, h bilan esa N nuqtadan α tekislikkacha bo’lgan masofani belgilaylik. 1-ta’rif. Berilgan γ chiziqdagi N nuqta M nuqtaga yaqinlashganda h d2 nisbat nolga intilsa, α tekislik γ chiziqning M nuqtasiga yopishma tekisligi deb ataladi (11-rasm). y− y y'(t)= x − x x ' ( t ) = z − z z ' ( t ) normali tenglamasi esa (x-x 0) x’(t)+(y-y 0 )y’(t)+(z-z 0 )z’(t)=0 ko’rinishda bo’ladi. Bu yerda x 0 =x(t 0 ), y 0 =y(t 0 ), z 0 =z(t 0 ). Regulyar egri chiziq y=y(x), z=z(x) tenglamalar yordamida berilsa, uning urinma tenglamasi y− y y'(x) = x − x 1 = z − z z ' ( x ) normali tenglamasi esa, x-x 0 +(y-y 0 )y’(t)+(z-z 0 )z’(t)=0 ko’rinishda bo’ladi. Agar fazodagi egri chiziq { φ ( x , y , z ) = 0 ω ( x , y , z ) = 0 Tenglamalar yordamida aniqlangan va ( φ φ φ ω ω ω ) matritsaning rangi ikkiga teng bo’lsa, M (x 0 , y 0 , z 0 ) nuqtadan o’tuvchi urinma tenglamasi x − x | φ φ ω ω | = y − y | φ φ ω ω | = z − z | φ φ ω ω | normali tenglamasi (x-x 0 ) | φ φ ω ω| +(y-y 0 ) | φ φ ω ω|+(z− z)| φ φ ω ω| =0 ko’rinishda bo’ladi. Bu yerda xususiy hosilalar M (x 0 , y 0 , z 0 ) nuqtada hisoblangan. Misol va masalalar yechish namunalari 1-masala. Tekislikda y=x 2 +4x+3 funksiyaning grafigidan iborat chiziq berilgan bo’lsin. Chiziqning absissasi x=-1 ga teng bo’lgan M nuqtadagi urinma va normali tenglamasini tuzing. (4-rasm) 1-masala. Ushbu { x= 3at t3−1 y= 3at 2 t3+1 tenglamalar sistemasi bilan berilgan chiziq (Dekart yaprog’i) ning asimptotalari topilsin. Yechish. Sistemaga tegishli tenglamalardan ko’rinib turibdiki, parametrning t=-1 qiymatida funksiyalar aniqlanmagan, ya’ni sistemadagi funksiyalarning maxrajlari nolga aylanadi, lekin suratlari chekli bo’ladi. Shuning uchun funksiyalar parametrning bu qiymatida cheksizlikka intiladi. Demak, parametrning qiymati -1 ga intilganda chiziq asimptotaga ega bo’ladi. Endi t → -1 uchun asimptotaning k burchak koeffitsiyenti va l ozod hadiniu topamiz: k= lim t → t 0 y ( t ) x ( t ) = limt→−1 3at 2 t3+1 3at t3+1 = lim t → − 1 t =-1, k=-1 l= lim t → t ( y ( t) − kx ( t)) = ¿ ¿ limt→−1 3at 2+3at t3+1 = limt→−1 3at (t+1) (t+1)(t2−t+1) = lim t → − 1 3 at t 2 − t + 1 = -a; l=- a. Yechish: shartga ko’ra, AB=a va OA= φτ , bunda τ =const. harakatdagi kesma boshlang’ich paytda Ox o’qida bo’ladi, deb faraz qilsak, vint chizig’idagi B nuqtaning vaziyati φ parameter bilan to’la aniqlanadi. Ushbu chiziq tenglamasini tuzamiz: OB= r = AB+OA. Ikkinchi tarafdan, AB=a(icos φ +j sin φ )=ae( φ ) va OA= τφk munosabatlarni hisobga olsak, vint chizig’i radius – vektorning ifodasini hosil qilamiz. Demak, vint chizig’ining tenglamasi r( φ )=ae( φ )+ τφ k yoki kordinata ko’rinishida II BOB. FRUNE FORMULALARI 2.1-§ Asimptotalar. Maxsus nuqtalar. Chiziqlarni tekshirish va yasash. O’rama . Differensial geometriyada o’rganilayotgan chiziqlar ichida bir tomonlama yoki ikki tomonlama cheksizlikka ketadigan chiziqlar tushunchasi kiritiladi. Bunday chiziqlarning cheksizlikka ketadigan shoxlari biror to’g’ri chiziqqa yaqinlashishsi mumkin. Yuqoridagi xossaga ega bo’lgan chiziqlarni yasash uchun , ularga shoxlari cheksizlikka intilganda yaqinlashadigan to’g’ri chiziqlarni bilish zarur bo’ladi. Shuning uchun chiziq asimptotalarini o’rganish muhim hisoblanadi. Bizga biror γ yopiq bo’lmagan egri chiziq o’zining biror parametrlash usuli x=x(t), y=y(t), (a ¿t<b ) bilan berilgan bo’lsin. 1-ta’rif. Berilgan chiziqning parametri t uchun ushbu t → a yoki t → b munosabatlardan faqat bittasi o’rinli ekanligidan x 2 (t)+y 2 (t) → ∞ munosabat kelib chiqsa, u holda berilgan chiziq bir tomonlama cheksizlikka intiladi deyiladi. Agar berilgan chiziqning parametri t uchun ushbu t→ a va t → b munoisabatlar birdaniga o’rinli bo’lganida x 2 (t)+y 2 (t) → ∞ munosabat bajarilsa, berilgan chiziq ikki tomonlama cheksizlikka intiladi deyiladi. 2-ta’rif. Berilgan γ egri chiziq parametrining t qiymatiga mos keluvchi M(t) nuqtasidan biror l to’g’ri chiziqqacha masofani d(t) kabi belgilaylik. Agar γ egri chiziq parametri t uchun t→ a munosabatdan ushbu d(t) → 0 munosabat kelib chiqsa, u holda l to’g’ri chiziq γ egri chiziqning asimptotsi deyiladi. 1-tasdiq. Biror parametrlash usuli x=x(t), y=y(t) (a ¿t<b ) bilan berilgan va t → a da cheksizlikka intiluvchi γ egri chiziq asimptotaga ega bo’lishi uchun , parametr t → a da b 1) Ushbu munosabatlardan biri y(t)(x(t)) -1 , x(t)(y(t)) -1 chekli limitga ega bo’lishi, aniqlik uchun y(t)(x(t)) -1 → k munosabat o’rinli bo’lishi; 2) Birinchi shart bajarilganda ushbu y(t)-kx(t) ifodaning biror limitga intilishi zarur va yetarli. Agar bu limitni l deb belgilasak, u holda y-kx-l=0 tenglama asimptota tenglamasi bo’ladi. Endi ordinata o’qiga parallel asimptotani qidiramiz. Berilgan chiziqning. Oy o’qiga parallel asimptotasi mavjuda deb faraz qilamiz. Chiziqning M nuqtasi cheksizlikka intilganda, y(t)= ∞ bo’lib, x(t) qandaydir bir o’zgarmas a songa intiladi. Bu a sonni lim t → x x ( t ) = x(t 0 )=a munosabatdan topamiz. U holda Oy o’qiga parallel asimptotaning tenglamasi x-a=0 ko’rinishida bo’ladi. 1-ta’rif. Berilgan γ chiziqdagi N nuqta M nuqtaga yaqinlashganda ∆φ ∆s ifodaning limiti mavjud bo’lsa, u γ chiziqning M nuqtadagi egriligi deb ataladi va k= limN→M ∆φ ∆S kabi belgilanadi (13-rasm). 2-ta’rif. Berilgan γ chiziqdagi N nuqta M ga yaqinlashganda ∆φ ∆s ifodaning limiti mavjud bo’lsa, u γ chiziqning M nuqtadagi absolut buralishi deb ataladi va [ σ ¿ = lim N → M ∆ φ ∆ S kabi belgilanadi. Xuddi shunga o’xshash, chiziqning Ox o’qiga parallel asimptotasini hosil qilish uchun, chiziqning M nuqtasi cheksizlikka intilganda, x(t)=∞ bo’lib, y(t0 qandaydir bir o’zgarmas b songa intiladi. Bu b sonni limt→by(t) =y(t 0 )=b munosabatlarni topamiz. U holda izlanga asimptotaning tenglamasi y-b=0 bo’ladi. 2-tasdiq. Berilgan chiziq bir (ikki) tomonlama chekssizlikka intilgnda uning urinmasining limiti mavjud bo’lsa, bu limit (limitlar) chiziq asimptotasi (asimptotalari) deyiladi. Teskarisi har doim ham o’rinli bo’lavermaydi, ya’ni chiziq asimptotasi mavjud bo’lib, u urinmaning limiti bo’lmasligi mumkin. Masalan, y= cos x x funksiya grafigidan iborat chiziq x → ∞ da Ox o’qidan iborat asimptotaga ega, lekin bu chiziq urinmasining burchak koeffitsiyenti y’=-2 sin x - cos x x esa x→ ∞ da hech qanday limitga intilmaydi. Chunki cos x x → 0 bo’lsada, sinx 2 ning limiti yo’q, u x→ ∞ da -1 va 1 sonlari orasida tebranib turadi. Matematik analiz kursidan y=f(x) ko’rinishidagi funksiya grafigini yasash usuli ma’lum. Endi biz F(x;y)=0 ko’rinishdagi tenglama bilan berilgan chiziqlarni yasash usulini keltiramiz. Biror tenglama bilan berilgan chiziqni yasash uchun uning: 1) Aniqlanish sohasini; 2) Koordinata o’qlari bilan kesishgan nuqtalarini; 3) Koordinata o’qlariga nisbatan simmetrikligini; 4) Koordinata o’qlariga parallel urinmalarini; 5) Maxsus nuqtalarini; 6) Egilish nuqtalarini; 7) Qavariq va botiqligini; 8) Asimptotalarini; 9) Mumkin bo’lgan hollarda bir nechta yordamchi nuqtalarni topish kerak. 3-ta’rif. Bizga bir (ikki) parametrli chiziqlar oilasi berilgan bo’lsin., ya’ni chiziq tenglamasida bitta ( ikkita) parameter qatnashsin. Ba’zan bunday oila uchun o’zining har bir nuqtasida oila chizig’iga urinadigan va shu urinish nuqtalaridan tashkil topgan chiziq mavjud bo’ladi. Bunday chiziq berilgan oila uchun o’rama deyiladi. Misol va masalalar yechish namunalari Tasdiq. Regular egri chiziq har bir nuqtasida yagona urinmaga ega. Agar γ egri chiziq ⃗r (t)= ⃗r tenglama bilan berilgan bo’lsa, M(t 0 ) nuqtadagi urinma ⃗r (t 0 ) vektorga parallel bo’ladi. Yuqoridagi tasdiqdan foydalanib urinma ta’rifini quyidagicha ifodalash mumkin. 2-ta’rif. Regulyar γ egri chiziq ⃗r = r (t) tenglama bilan aniqlansa, M (t 0 ) nuqtadan o’tuvchi va ⃗r ’(t 0 ) vektorga parallel to’g’ri chiziq γ ning M(t 0 ) nuqtasida o’tkazilgan urinmasi deyiladi. 3-ta’rif. Egri chiziqning M nuqtasidan o’tuvchi va urinmaga perpendicular ravishda o’tadigan tekislik egri chiziqning M nuqtasidagi normali deyiladi. Izoh. Masala tekislikda qralayotgan bo’lsa, egri chiziqning normali to’g’ri chiziqdan iborat bo’ladi. Regulyar γ egri chiziq ⃗r = r (t) tenglama bilan aniqlansa, uning M(t 0 ) nuqtasida o’tkazilgan urinma tenglamasi ⃗ρ (t)= ⃗r (t 0 )+ τ⃗r ’(t 0 ) normali tenglamasi ( ⃗ρ (t)- ⃗r (t 0 ) ⃗r ’(t 0 )=0 ko’rinishda bo’ladi. Regulyar egri chiziq parametric tenglamalar yordamida, ya’ni { x= x(t) y= y(t) z= z(t) a ¿ t ¿ b sistema yordamida aniqlangan bo’lsa, M(t 0 ) nuqtadan o’tuvchi urinma tenglamasi yuqoridagi topilganlarini e’tiborga olib asimptta tenglamasi x+y+a=0 ko’rinishda ekanligini aniqladik. Berilgan chiziqning Oy va Ox o’qlariga parallel asimptotalari yo’qligi ravshan (6-rasm). 2-masala. Ushbu (x-C) 2 +y 2 =36 tenglama bilan berilgan aylanalar oilasining o’ramasi topilsin. Yechish. Berilgan tenglamadan C bo’yicha hosila olib, hosil bo’lgan tenglamani (x-C) 2 +y 2 =36 tenglama bilan birgalikda yechib, y=±6 tenglikni olamiz. Demak, aylanalar oilasining discriminant chizig’i y= ±6 to’g’ri chiziqlardan iborat ekan. Bu discriminant chiziq bilan berilgan aylanalar oilasining o’ramasi bo’ladi (8-rasm). 3-masala. Ushbu (y-C) 3 -y 2 =0 yarim kubik parabolalar oilasining o’ramasi topilsin. Yechish. Bu oilaning o’ramasini topish uchun ta’rifga ko’ra berilgan oila tenglamasidan C parameter bo’yicha hosila olamiz va oila tenglamasi bilan birgalikda yechib x=0 to’g’ri chiziq tenglamasini hosil qilamiz. Bu chiziq berilgan oilaning o’ramasini bermaydi. Chunki, x=0 to’g’ri chiziq oila maxsus nuqtalardan tashkil topgan (9-rasm). Ta’limni tubdan isloh qilishning ajralmas va muhim qismi hisoblangan zamonaviy pedagogik texnologiyalar, interfaol metodlar, amaliyotga joriy qilinishi mumkin bo’lgan yo’l-yo’riqlar yangicha usullar orqali mutaxassislar tomonidan ma’lum tizim asosida o’rgatilishi lozim. Jahon ta’limi tajribasi shundan dalolat beradiki, jamiyat taraqqiyoti ta’limning takomillashishi va taraqqiy qilishi bilan chambarchas bog’liqdir. Prezident Islom Karimovning O’zbekiston Respublikasi Konstitutsiyasining 20 yilligiga bag’ishlangan tantanali marosimda “Inson manfaati, huquq va erkinliklarini ta’minlash, hayotimizning yanada erkin va obod bo’lishiga erishish – bizning bosh maqsadimizdir” mavzusida qilgan ma’ruzasida jumladan shunday fikrlarni o’qish mumkin: “Bu yo’lda bizning eng katta tayanch va suyanchimiz, hal qiluvchi kuchimiz yosh avlodimizdir. Bu – O’zbekistonda tashkil etilgan dunyo miqyosida katta qiziqish va havas uyg’otayotgan mutlaqo yangi o’quv tizimida yuksak ta’lim-tarbiya olayotgan, eski asoratlardan, qarashlardan uzoq bo’lgan, zamonaviy kasb- hunarlarni o’zlashtirgan, mustaqil fikrlaydigan, ertangi kunga intilayotgan bizning farzandlarimizdir. ... Ishonchim komil, bunday yoshlarimizning safi qancha ko’paysa, qancha rivoj topsa, hech shubnasiz, marra bizniki, O’zbekistonnikidir” 1 Mustaqillik yillarida ta’lim tizimidagi o’zgarishlar ta’lim jarayoni tarkibiy qisimlarini yangicha tartibda namoyon bo’lishini taqozo etadi. An’anviy ta’lim qonuniyatlari va tamoyillariga mos holda yangi tamoyillarga amal qilish, ta’lim metodlarining paydo bo’lishi, ta’lim vositalarining takomillashuvi, ayniqsa ta’limni tashkil etishning noan’anaviy shakllari keng ko’lamda joriy etilishi kuzatilmoqda. Mazkur o’zgarishlarning bir qismi mavjud didaktik ta’limotlarning tarkibidan o’sib chiqqan bo’lsa, yana bir qismi dunyodagi ta’lim tizimi rivojlangan mamlakatlar olimlarining pedagogik tajribalariga suyangan holda paydo bo’ladi. Shu o’rinda ta’limning zamonaviy interfaol metodlarining mamlakatimiz ta’lim sohasiga kirib kelishi alohida e’tibor qaratadigan yo’nalishlardan biri ekanligini qayd etish zarur. Mavzuning dolzarbligi – Ta`lim jarayoni interfaol metodlar asosida tashkil etish bo’lajak mutaxassislarning O’zbekistoning ilg’or tajribalari, an’analari, madanyatini hisobga olgan holda har tomonlama shakllantirish imkonyatini beradi. Bu borada ta’lim tizmida, oquv jarayonida interfaol metodning umumiy asoslari tadqiq etilgan. Pedagogik olimlar O. Tolipov, SH. Abdullaeva, O. Haydarova kabilarning tadqiqot ishlari shular jumlasidandur. Ta’lim jarayoni ko’p bosqichli 1.4-§. Misol va masalalar yechish 1. Beriligan ikki nuqtagacha masofalari kvadrastlari o’zgarmas songa teng bo’lgan nuqtalarning geometric o’rni topilsin. 2. Berilgan ikki nuqtagacha masofalari kvadratlari ayirmasi o’zgarmas songa teng bo’lgan nuqtalarning geometric o’rni topilsin. 3. Ixtiyoriy nuqatadan A(4;0) nuqtagacha bo’lgan masofa B(1;0) nuqtagacha bo’lgan masofadan ikki marta kata bo’lgan nuqtalarning geometric o’rni topilsin. 4. Katetlari a, b ga teng to’g’ri burchakli uchburchak harakat qilganda uning o’tkir burchakli uchlari o’zaro perpendicular to’g’ri chiziqlar bo’yicha sirpanadi. Bu harakat natijasida uchburchak to’g’ri burchagining uchi chizadigan chiziq tenglamasini tuzing. 5. Tekislikdagi umumiy dekart koordinatalar sistemasining Ox, Oy o’qlarida A, B nuqtalar berilgan bo’lsin. Berilgan A, B nuqtalardan o’tuvchi AB to’g’ri chiziqda yotgan P(x 0, y 0 ) nuqtadan Ox, Oy o’qlari mos ravishda C, D nuqtalalrdan kesib o’tadigan ixtiyoriy kesuvchi o’tkaziladi. So’ngra CB, AD to’g’ri chiziqlarning kesishish nuqtasi M bilan belgiilangan bo’lsin. Kesuvchi to’g’ri chiziq P nuqta atrofida aylanganda M nuqta chizgan chiziq tenglamasini tuzing. 6. Berilgan uchta nuqtagacha bo’lgan masofalar kvadratlarining yig’indisi o’zgarmas bo’lgan nuqtalarning geometrik o’rni topilsin. 7. To’g’ri to’rtburchak tomonlarigacha masofalari kvadratlari yig’indisi o’zgarmas bo’lgan nuqtalarning geometrik o’rni topilsin . 8. Ikkita aylana berilgan bu aylanalarga o’tkazilgan urinmalar uzunliklari bir xil bo’ladigan nuqtalarning geometric o’rni topilsin. 9. Markazi koordinata boshida bo’lgan aylana berilgan. Agar aylanada yotgan barcha nuqtalarning ordinatalarini k marta kamaytirilsa, qanday chiziq hosil bo’ladi. 10. Aylananing belgilangan yo’nalishga parallel vatarlarini berilgan nisbatta bo’ladigan nuqtalarning geometric o’rni topilsin. 11. Markazlari O koordinata boshida, radiuslari a, b ga teng aylanalar berilgan. Uchi koordinata boshida bo’lgan nur O nuqta atrofida aylanish natijasida berilgan aylanalarni mos ravishda A, B nuqtalarda kesib o’tadi. Hosil bo’lgan B nuqtadab absissa o’qiga parallel to’g’ri chiziq o’tkazildi. A nuqtadan esa ordinate o’qiga parallel to’g’ri chiziq o’tkaziladi. Bu ikki to’g’ri chiziqlarning kesishish nuqtasini M bilan belgilaylik. Hosil bolgan M nuqtalarning geometric o’rni topilsin. {τ = k ϑ ϑ = − kτ − σβ β = σ ϑ . [X − x ( t ) Y − y ( t ) Z − z ( t ) x ' ( t ) y ' ( t ) z ' ( t )| y ' ( t ) z ' ( t ) y ' ' ( t ) z ' ' ( t ) | | z ' ( t ) x ' ( t ) z ' ' ( t ) x ' ' ( t ) | | x ' ( t ) y ' ( t ) x ' ' ( t ) y ' ' ( t ) |] =0 bo’ladi. Urinma, bosh normal, binormal bo’yicha yo’nalgan birlik vektorlardan tashkil topgan uchlik Frene bazisi deyiladi(12-rasm). Ularni mos ravishda quyidagi formulalar bo’yicha topiladi: τ= ⃗r ¿¿ ; α = [ [ r ' , r ' ' ] r ' ' ] [ [ r , r ' ] r ' ] ; β = r ' , r ' ' r , r ' . 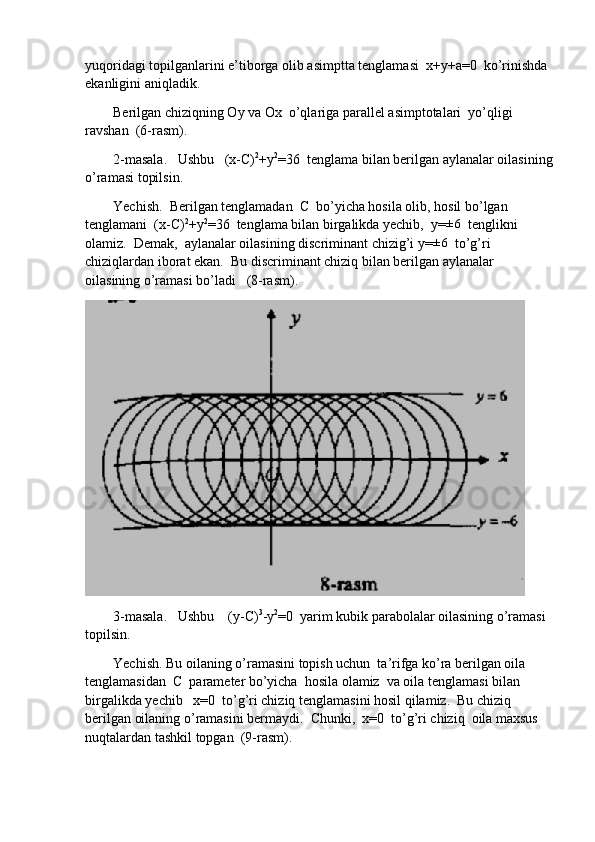2.3-§. Egri chiziq egriligi va buralishi. Frene formulalari Bizga γ egri chiziq va M unga tegishli nuqta berilgan bo’lsin. Berilgan egri chiziqda M nuqtaga yaqin N nuqta olib, bu nuqtalarda o’tkazilgan urinmalar orasidagi burchakni ∆φ bilan, MN yoy uzunligini ∆s bilan belgilaylik. yaxlit tizimga ega bolib, uning har bir bosqichi ta’lim oluvchilarning yoshi va oziga xos xususiyati ta’lim–tarbya jarayonida intelektual qobiliyatiga bog’liqdir. O’quvchi o’quvchilikka qabul qilingandan boshlab har bir fanning ilmiy–nazariy asoslarni chuqur o’rganish bilan birga kasb tayyorgarligiga alohida e’tibor qaratildi. Jamyatning intelektual salohiyotiga mos kelajak avlodni tarbyalash bugungi ta`lim tizimi oldida turgan dolzarb vazifa bo’lib, bu o’z navbatida ta’lim jarayonida mumtazam ravishda innovatsion yondashuvlarni amalga oshirishni talab etadi. Innovatsion yondashuvlar - ta’lim jarayonida zamonaviy pedagogik texnologiyalarni qo’llash demakdir. Mazkur kurs ishimning mavzusining dolzarbligi ham mana shunda. Matematikani o’qitish umumiy sistemasida masalalar yechish samarali mashq turlaridan biridir. Masalalar yechish bolalarda avvalo mukammal matematik tushunchalarni shaklllantirish ularning programmada berilgan nazariy bilimlarni o’zlashtirishlarida favqulotda muhim ahamiyatga ega. Masalan, agar biz qo’shish haqida to’g’ri tushuncha shakllantirishni istasak, buning uchun bolalar yig’indini topishga doir yetarli miqdorda sodda masalalarni deyarli har gal to’plamlarni birlashtirish amalini, bajarib yechishlari zarur. Shunday qilib, masalalar konkret material bo’lib, ular yordamida bolalarda yangi bilim vujudga keladi va mavjud bilimlar tadbiq qilinishi jarayonida mustahkamlab boradi. Masalalar bilimlarni shakllantirishda konkret material bo’lgani holda nazariyani amaliyot bilan, o’qitishni turmush bilan bog’lab olib borish imkonini beradi. Masalalar yechish bolalarda kundalik hayotda har bir kishi uchun zarur bo’lgan amaliy uquvlarni vujudga keltiradi. Tadqiqotning maqsadi: Egri chiziqning egriligi va buralishiga doir masalalarni ishlash samaradorligini oshirishda zamonaviy pedagogik texnologiyalar va ularni qo’llash usullarini ishlab chiqish, dastur materiallariga mos masalalarni o’rganishning samarali usullarini aniqlash yangi pedagogok texnologiyalardan foydalanib masala yechishni amalga oshirish yo’llarini izlashdan iborat. Tadqiqot ob’yekti: Egri chiziqning egriligi va buralishiga doir masalalar ustida ishlash usullari va matematika darslarida zamonaviy texnologiyalarni qo’llash jarayoni. Tadqiqotda qo’yilgan asosiy masalalar: 1. Egri chiziqning egriligi va buralishiga doir masalalarni yechish usullarini tahlil qilish. 2. Egri chiziqning egriligi va buralishiga doir masalalar mazmunini tahlil qilish. 3. Ilg’or o’qituvchilarining tajribalarini o’rganish. 4. Egri chiziqning egriligi va buralishiga doir masalalarni o’rganish bo’yicha pedagogic tajriba o’tkazish, natijalarini metodik tavsiya sifatida bayon qilish. Egri chiziqning egriligi va buralishi MUNDARIJA KIRISH …………………………………………………………………………3 I BOB. CHIZIQLAR NAZARIYASI …………………………………………. 1.1-§. Egri chiziq va uning berilish usullari……………………………….... 1.2-§. Vektor funksiyalar uchun differensial hisob…………………………. 1.3-§. Egri chiziq urinmasi va normali……………………………………..... 1.4-§. Misol va masalalar yechish………………………………………….. I BOB. FRUNE FORMULALARI… …………………………………………… 2.1-§. Asimptotalar.Maxsus nuqtalar.Chiziqlarni tekshirish va yasash. O’rama............................................................................................... 2.2-§. Frene bazisi. Egri chiziqning tabiiy parametrizatsiyasi………………….. 2.3-§. Egri chiziq egriligi va buralishi. Frene formulalari………………………. XULOSA …………………………………………………………………………. FOYDALANILGAN ADABIYOTLAR ………………………………………….. Kirish. O‘ZBEKISTON RESPUBLIKASI OLIY TA’LIM, FAN VA INNOVATSIYALAR VAZIRLIGI __UNIVERSITETI Ro’yxatga olindi №__________ Ro’yxatga olindi №__________ “_____” ____________20 y. “_____” ____________20 y. “___________________________ “ KAFEDRASI “_____________________________ “ FANIDAN KURS ISHI Mavzu:________________ Bajardi:_________________________________ Tekshirdi:_______________________________ ______________ - 20___ U holda 0= d du| r| 2 = d du ( ⃗r , ⃗r )= 2( ⃗r , ⃗r u ) 0= d dv | r| 2 = d du ( ⃗r , ⃗r ) = 2( ⃗r , ⃗r v ) Tengliklardan ushbu ( ⃗r , ⃗r u )= ( ⃗r , ⃗r v )=0 tengliklar kelib chiqadi. Yetarliligi. Endi ⃗r \\ ⃗r u , ⃗r \\ ⃗r v deb faraz qilaylik. U holda d du | r| 2 = 2( ⃗ r , ⃗ r u )=0 d dv | r| 2 = 2( ⃗ r , ⃗ r u )=0 Tengliklardan ⃗r (u, v) funksiyaningn o’zgarmas ekanligi kelib chiqadi. Masala to’liq yechildi. 1.3-§. Egri chiziq urinmasi va normali Egri chiziq urinmasi tushunchasi dastlab maktab kursida o’tiladi. Birinchi kursda esa xususiy holler, ikkinchi tartibli chiziqlar va sirtlarga o’tkazilgan urinma tushunchasi o’rganiladi. Differensial geometriya va topologiya fanida avval urinmaning umumiyroq, lekin klassik ta’rifi orqali, xossalari o’rganiladi. Sirtlar nazariyasida esa urinma tushunchasi urinma vector orqali aniqlanadi. Keyinchalik bu tushuncha ko’pxillikning urinma fazosini aniqlash uchun kerakli muhim tushuncha ekanligi amalda ko’rsatiladi. Bizga γ elementar chiziq va M nuqta berilgan bo’lsin. Berilgan chiziqning M nuqtasiga o’tkazilgan urinma tushunchasini kiritamiz. Buning uchun M nuqtadan l to’g’ri chiziqni o’tkazaylik, N bilan M ga yaqin bo’lgan γ elementar chiziqning birorta nuqtasini belgilaylik. Egri chiziqdagi M va N nuqtalar orasidagi masofani d bilan, N nuqtadan l to’g’ri chiziqqacha bo’lgan masofani h bilan belgilaylik. 1-ta’rif. Berilgan γ egri chiziqning N nuqtasi M nuqtasiga intilganda h d ifoda nolga intilsa, l to’g’ri chiziq γ egri chiziqning M nuqtasida o’tkazilgan urinmasi deyiladi. (3-rasm) Yechish. Avvalo M nuqtaningb ordinatasini topamiz: y 0 =(-1) 2 +4·(-1)3=0. Endi chiziqning pametrik tenglamalarini { x=t y=t+4t+3, − ∞ < t < + ∞ ko’rinishda yozib, t=-1 nuqtadagi hosilalarning qiymatlarini hisoblaymiz. x’(-1)=1, y’(-1)=2. Natijada chiziqning urinmasi va normali tenglamalarini mos ravishda ushbu ko’rinishda x + 1 1 = y 2 va x + 1 − 2 = y 1 yoza olamiz. Chiziq tenglamasi vektor ko’rinishda ⃗ r = {t;t2+4t+3} tenglama bilan berilgan bo’lsa, urinma va normali tenglamalarini vector ko’rinishda mos ravishda quyidagicha ifodalash mumkin: ⃗ ρ = { − 1 ; 0 } +{ − 2 ; 1 } ω ⃗ ρ = { − 1 ; 0 } +{ − 2 ; 1 } ω Xulosa Biz bu kurs ishida differensial geometriya kursining asosiy tushunchalaridan bo’lgan egri chiziq tushunchasini kiritdik va ularning tenglamalarini ba’zi bir xususiyatlarini topishga doir misol va masalalar keltirdik. Bundan tashqari differensial geometriya va topologiya fanida vector analizi muhim o’rin tutadi. Shuning uchun vector funksiyalar xossalariga doir misol va masalalar keltirilgan. Egri chiziq urinmasi tushunchasi maktab kursida kiritiladi. Birinchi kursda esa xususiy hollar, ikkinchi tartibli chiziqlar va sirtlarga o’tkazilgan urinma tushunchasini o’rgandik. Differensial geometriya va topologiya fanida avval urinmaning umumiyroq, lekin klassik ta’rifi orqali, xossalari o’rganiladi. Sirtlar nazariyasida esa urinma tushunchasi urinma vector orqali aniqlanadi. Keyinchalik bu tushuncha ko’pxillikning urinma fazosini aniqlash uchun kerakli muhim tushuncha ekanligi amalda ko’rsatiladi. Egri chiziq egriligi va buralishi differensial geometriyada o’rganiladigan chiziqlarning muhim hususiyatlaridan hisoblanadi. Bu xususiyatlarning mexanika va fizikadagi tatbiqlari ham mavjud. Bu tatbiqlarni xususan, Frene formulalarining ifodasida ham ko’rish mumkin. Foydalanilgan adabiyotlar: mavjud bo’lsa, uni r’(p) bilan belgilaymiz va r(p) vector funksiyaning p nuqtadagi hosilasi deb ataymiz. Tekislikdagi biror soha vector funksiya aniqlangan G to’plam sifatida olingan bo’lsa, u sohadagi nuqta uchun p=(u, v) belgilash kiritamiz. Bu holda r(p) va uning koordinata funksiyalari x(u, v), y(u, v), z(u, v) ikki o’zgaruvchili funksiyalar bo’ladi. Yuqoridagi funksiya tushunchasidan foydalanib, ⃗r u (u,v)={x u (u,v), y u (u,v) z u (u,v)} va ⃗r v (u,v)={x v (u,v), y v (u,v) z v (u,v)} tengliklarni hosil qilamiz. Bir o’zgaruvchili ⃗r (t) vector funksiya uchun integral tushunchasini kiritaylik. Agar ⃗r (t) vector funksiya uchun differensiallanuvchi ⃗ρ (t) vector funksiya mavjud bo’lib , ⃗r (t)= ⃗ρ' (t) tenglik bajarilsa, ⃗ρ (t) vector funksiya ⃗r (t) vector funksiyaning aniqmas integrali deyiladi va quyidagi ko’rinishda yoziladi: ρ (t) = ∫ ⃗ r ( t ) d(t) Masala. Bizga tekislikdagi biror g sohada aniqlangan differensiallanuvchi ⃗ r (u, v) vector funksiya berilgan bo’lsin. Berilgan vector funksiyaning uzunligi o’zgarmas bo’lishi uchun ( ⃗ r , ⃗ r u )= ( ⃗ r , ⃗ r v )=0 tengliklarning bajarilishi zarur va yetarli ekanligini isbotlang (2-rasm). Yechish: Zarurligi. Tasdiqni zarurligini isbotlash uchun |⃗ r| 2 =( ⃗ r , ⃗ r ) tenglikdan foydalanamiz. Berilgan vector funksiyaning uzunligi o’zgarmas deb faraz qilaylik, ya’ni |⃗ r ( u , v ) | =const. tenglik bajarilsin. 12. To’g’ri burchakli koordinatalar sistemasining koordinata o’qlari va ularni kesib o’tuvchi chiziqlqardan hosil bo’lgan o’zgarmas S yuzali to’g’ri burchakli uchburchaklarning to’g’ri burchagi uchuidan gipotenuzasiga perpendicular tushirilgan. Perpendicular asosining geometrik o’rni topilsin. 13. To’g’ri to’rtburchakning ikki o’qi koordinata o’qlari bilan ustma-ust tushadi. To’g’ri to’rtburchak diogonalining uzunligi o’zgarmas l ga teng bo’lib, qolaveradigan holda shaklan o’zgaradi. Koordinata boshiga qarama-qarshi uchidan diogonalga tushirilgan perpendicular asoslarining geometric o’rni astroida deb ataladi. To’g’ri to’rtburchakning qo’zg’almas tomonlarini koordinata o’qlari sifatida olib, astroida tenglamasi tuzilsin. 14. Qutb o’qiga perpendicular bo’lgan va undan OA=a ga teng kesma airatgan to’g’ri chiziqning qutb koordinatalar sistemasidagi tenglamasi tuzilsin. 15. Berilgan ikki aylanaga urinadigan aylananing markazlari geometric o’rni topilsin. Quyidagi hollar qaralsin: 1. Berilgan aylanalardan biri ikkinchisining ichida yotadi. 2. Berilgan aylanalardan biri ikkinchisining ichida yotmaytdi. 16. Radiusi a ga teng bo’lgan aylananing O nuqtasini qutb , OA diametrini qutb o’qi sifatida olib aylananing qutb koordinatalar sistemasidagi tenglamasi tuzilsin. 17. Radiusi a ga teng bo’lgan aylanada O nuta olingan bo’lib va bu nuqtaga diametral qarama-qarshi bo’lgan K nuqtada urinma o’tkazilgan. Olingan O nuqta atrofida to’g’ri chiziq aylanadi va u aylana bilan urinmani mos ravishda A, B nuqtalarda kesib o’tadi. A nuqtadan urinmaga parallel B nuqtadan OK diametrga parallel to’g’ri chgiziq o’tkaziladi. Bu to’g’ri chiziqlar kesishish nuqtalarining geometric o’rni topilsin. Koordinatalar boshi deb O nuqta, abscissa o’qi sifatida OK diametr olinsin. Hosil nbo’lgan chiziq Mariya Anezi zulfi deb ataladi. 18. Uzunligi 2a gating kesmaning uchlari to’g’ri burchak tomonlari bo’ylab sirpanadi. To’g’ri burchak uchidan kesmaga tushirilgan perpendicular asosining geometric o’rni ( bu chiziq to’rt yaproqli gul deb ataladi) tenglamasi qutb va dekart koordinatalar sistemalarida tuzilsin. 19. Radiusi a ga teng bo’lgan aylanada O nuqta olingan va bu aylanada nuqtaga diametral qarama-qarshi bo’lgan K nuqtadan aylanaga urinma o’tkazilgan. Olingan O nuqta atrofida nur aylanadi. Bu nur aylana va urinmani mos ravishda A, B nuqtalarda kesib o’tdi. Bu nurda urinma va aylana orasida joylashgan kjesma uzunligiga teng OM=AB kesma qo’yiladi. Nur aylanadagi M nuqtaning geometric o’rni Diokles sissoidasi deyiladi. Qutb deb O nuqtani va OK nurni qutb o’qi sifatida olib sissoidaning qutb Tasdiq. Ikki marta differensiallanuvchi regulyar γ egri chiziqning har bir nuqtasidan o’tuvchi yopishma tekislik mavjud bo’lib, urinma yopishma tekislikda yotadi. Agar egri chiziq ⃗r = ⃗r (t) tenglama yordamida aniqlangan bo’lsa, M(t 0 ) nuqtadan o’tuvchi yopishma tekislik ⃗r' (t 0 ), ⃗r'' (t 0 ) vektorlarga parallel bo’ladi. Izoh. Yopishma tekislik ⃗r' (t 0 ) va ⃗r'' (t 0 ) vektorlarga parallel bo’lganligi uchun , agar bu vektorlar o’zaro parallel bo’lsa, M(t 0 ) nuqtadan o’tuvchi yopishma tekisliklar cheksiz ko’p. Lekin, ⃗r' (t 0 ) va ⃗r'' (t 0 ) parallel bo’lmasa, M(t 0 ) nuqtadan o’tuvchi yopishma tekislik yagonadir. Ushbu ⃗r = ⃗r (t) tenglama bilan berilgan γ chiziqning M(t 0 ) nuqtasida o’tkazilgan yopishma tekislikning vector tenglamasi ( ⃗R - ⃗r (t 0 ), ⃗r' (t 0 ), ⃗r'' (t 0 ))=0 ko’rinishda bo’ladi. Agar egri chiziq x=x(t), y=y(t), z=z(t) parametric tenglamalar bilan berilsa, yopishma tekislik tenglamasi [ X − x Y − y Z − z x ' ( t ) y ' ( t ) z ' ( t ) x ' ' ( t ) y ' ' ( t ) z ' ' ( t ) ] =0 koordinatalar sistemasidagi tenglamasi tuzilsin, keyin dekart koordinatalar sistemasiga o’tilsin. 20. Qutb sifatida qo’zg’almas K nuqta va qutb o’qi sifatida qo’zg’almas nuqtani aylana markazi bilan tutashtiruvchi to’g’ri chiziq olingan holda, qo’zg’almas K nuqtadan berilgan ayl;ana urinmalariga o’tkazilgan perpendicular asoslarining geometric o’rni tenglamasi qutb koordinatalar sistemasida tuzilsin. Bunda qo’zg’almas K nuqtadan aylana markazigacha masofa a ga teng va aylana radiusi b ga teng deb olinsin.

Egri chiziqning egriligi va buralishi

KIRISH…………………………………………………………………………3

I  BOB. CHIZIQLAR NAZARIYASI………………………………………….

1.1-§. Egri chiziq va uning berilish usullari………………………………....

1.2-§. Vektor funksiyalar uchun differensial hisob………………………….

1.3-§. Egri chiziq urinmasi va normali…………………………………….....

1.4-§. Misol va masalalar yechish…………………………………………..

I  BOB. FRUNE FORMULALARI………………………………………………

2.1-§. Asimptotalar.Maxsus nuqtalar.Chiziqlarni tekshirish va yasash.

O’rama...............................................................................................

2.2-§. Frene bazisi. Egri chiziqning tabiiy parametrizatsiyasi…………………..

2.3-§. Egri chiziq egriligi va buralishi. Frene formulalari……………………….

XULOSA………………………………………………………………………….

FOYDALANILGAN ADABIYOTLAR…………………………………………..

 

Купить