Affin fazolarda to`gri chiziq v tekislikga doir metrik masalalar kurs ishi - Algebra - Kurs ishlari

Dokument ma'lumotlari

Narxi	30000UZS
Hajmi	772.5KB
Xaridlar	0
Yuklab olingan sana	03 Iyun 2025
Kengaytma	docx
Bo'lim	Kurs ishlari
Fan	Algebra

Sotuvchi

G'ayrat Ziyayev

Ro'yxatga olish sanasi 14 Fevral 2025

82 Sotish

Affin fazolarda to`gri chiziq v tekislikga doir metrik masalalar kurs ishi

Sotib olish

O‘ZBEKISTON RESPUBLIKASI OLIY TA’LIM,
FAN VA INNOVATSIYALAR VAZIRLIGI
Farg’ona davlat universiteti
Fizika-matematika fakulteti
Matematika yo`nalishi 1- kurs 24.02- guruh talabasi
Nu`monjonova Xuriyatxonning Analitik geometriya fanidan
“ Affin fazolarda to`gri chiziq v tekislikga doir metrik
masalalar ” mavzusi
KURS ISHI
Kurs ishi rahbari: B. Toshbuvayev
Farg’ona-2025
MUNDARIJA

KIRISH. …………………………………………………………………………….. 3
I BOB . AFFIN FAZOLAR ……………………………………………….................7
1 -§. Chiziqli fazo…………………………………………………………………….. 7
2-§. n o‘lchovli affin fazo. Affin koordinatalar sistemasi ……………........................9.
3-§. n o‘lchovli affin fazolarning izomorfligi……………………………………... 15
II BOB. AFFIN FAZOLARDA TO‘G’RI CHIZIQ VA TEKISLIK ……………18
1-§. Affin fazolarda tekislik…………………………………………....................... 18
2-§. Affin fazolarda to‘g’ri chiziq…………………………………………………. 27
3-§. Affin fazoda to‘g’ri chiziq va tekislikning o‘zaro vaziyati……………………33
XULOSA …………………………………………………………………………..36
FOYDALANILGAN ADABIYOTLAR………………………………………....37

KIRISH
Matematika hamma aniq fanlarga asos. Matematikani
yaxshi bilgan bola aqlli, keng tafakkurli bo‘lib o‘sadi va
istalgan sohada muvaffaqiyatli ishlab ketadi.
SH.M.Mirziyoyev
Ilm o‘rganish har bir inson uchun hayot yo‘llarida asqotadigan, odamlar
orasida uni ajratib turadigan, yolg’iz qolgan paytlarida yo‘ldosh bo‘lib, tushkunlikka
tushganida doimo madadkor bo‘luvchi yengilmas quroldir. Shu nuqtai nazardan
bugun har birimiz ilm olishimiz, mukammal bilim egallab, kasb-hunar o‘rganishimiz
va bu orqali o‘z kelajagimizni o‘zimiz yaratib, mamlakatimiz gullab yashnashi,
ravnaq topishi uchun o‘z hissamizni qo‘shishimiz zarurdir.
Kurs ishining dolzarbligi: Talabalar intellektual tafakkurini shakllantirish
asosida talabalar qobiliyat va qiziqishlarini rivojlantirish ularning “Affin fazolarda
to‘g’ri chiziq va tekislikga doir metrik masalalar” mavzulari bo‘yicha bilimlarni
yanada chuqurlashtirish. Mamlakatimizda hozirgi paytda yoshlarga ta’lim-tarbiya
berishga alohida e’tibor qaratilmoqda. Ta’lim tarbiya hamisha jamiyat
taraqqiyotining asosi bo‘lgan. Chunki, inson jamiyatdagi barcha munosabatlar,
aloqalarning markazida turadi. Fan-texnika va axborotdagi revolyutsiya inson va
uning ilmiy-ma’rifiy potensialini ijtimoiy-iqtisodiy taraqqiyotning hal qiluvchi
omiliga aylantiradi. Kelajakda erishishimiz lozim bo‘lgan buyuk maqsadlarga
erishish uchun , avvalo , yuqori malakali, zamon talabiga javob beradigan mutaxassis
kadrlar tayyorlashimiz kerak.
O‘zbekiston Respublikasining “Ta’lim to‘g’risida”gi qonuni va “Kadrlar
tayyorlash milliy dasturi” xalqaro ta’lim standartlarini mamlakatimiz oliy ta’lim
tizimiga joriy qilish, yuqori malakali zamonaviy kadrlar tayyorlashda milliy an’ana
va tajribalarimiz bilan birga ilg’or jahon tajribalaridan keng foydalanish borasida
yangi imkoniyatlar taqdim etayotganligi barchamizga ma’lum. Shu jumladan,
yurtimizda matematikani rivojlantirishga qaratilgan ko‘plab chora-tadbirlar amalga
oshirilayotganligining guvohimiz.

Matematika aniq bir bilim sohasi va turli sohalarga chuqur kirib borayotgan
universal vosita bo‘lib qolmasdan sivilizatsiyaning ajralmas qismi, umuminsoniy
madaniyatning muhim elementi hamda dunyoni ilmiy o‘rganish tilidir. Matematik
bilim hayot sirlarini o‘rganishda, kasb tanlashda muhim bo‘lgani bois fikrlash
madaniyati tarkibidagi qat’iylik, aniqlik, izchillik, mantiqiylik va asoslanish singari
qirralarining shakllanishiga xizmat qiladi. Ulkan iqtisodiy o`zgarishlar yuz
bеrayotgan hozirgi davrda matеmatikaning ahamiyati yanada oshdi, shuning uchun
ham matеmatik ta’lim katta ijtimoiy ahamiyatga ega. Rеspublikamiz hukumati
yoshlarga ta’lim va tarbiya bеrish tizimini takomillashtirish, ta’lim va tarbiyani
turmushning oshib borayotgan talablari darajasiga yеtkazish vazifasini qo`ydi.
Ma’lumki o‘quvchilarning fikrlash qobiliyatlarini rivojlantirish har bir fan
oldidagi muhim masalalardan hisoblanadi. Jumladan umumiy o‘rta ta’lim
maktablarida o‘quvchilarning intellektual qobiliyatlarini rivojlantirish dolzarb
masaladir. Shu bois geometriya o‘qitish jarayonida har bir o‘quvchining intellektual
qobiliyatlarni rivojlantirish muammosi o‘zining strukturasi jihatidan ancha murakkab
bo‘lib, uning tarkibida matematik qonuniyatlar, faktlar, munosabatlar asosida yuzaga
kelishi tabiiy holdir. Shuning uchun ham har bir o‘quvchi geometriya darslarida
geometrik obrazlar bilan ish ko‘radi, chunki undagi o‘lchamlarni, kattaliklarni sezadi
va bu kattaliklar orasidagi mavjud qonuniyatlarni idrok etadi, o‘z tasavvuriga tegishli
geometrik obrazlarni keltirib va bularni mushohada asosida o‘z in’nikosiga o‘tkazadi.
Geometriya kursida geometrik obrazlarni ko‘p holda ideal ko‘rinishda tasavvuriga
keltiriladi va shunday tafakkur qilinadi.
Affine fazolarni o‘rganishda to‘g’ri chiziqlar va tekisliklar o‘rtasidagi o‘zaro
munosabatlarni tahlil qilish muhim o‘rin tutadi. Bu fazolar o‘zaro affine
transformatsiyalar yordamida o‘zgaradi, ya’ni chiziq yoki tekisliklarning shakli,
orientatsiyasi va o‘lchamlari transformatsiyalar orqali o‘zgartiriladi, ammo ularning
relative joylashuvi va nisbiy masofalari saqlanadi. Bu o‘zgarishlarni tahlil qilish esa
ko‘plab amaliy masalalar, jumladan, kompyuter grafikasi, robototexnika, fizik
modellashtirish va boshqa ilmiy-texnikaviy sohalarda qo‘llaniladi.

Affine geometriya o‘rganiladigan asosiy obyektlardan biri – to‘g’ri chiziqlar
bo‘lib, ular bir nuqtadan boshqasi orqali o‘tuvchi va teng masofali nuqtalarni
bog’laydigan geometrik obyektlardir. To‘g’ri chiziqlar o‘rtasidagi masofani
hisoblash, affine fazolarda ularning orientatsiyasi va joylashuvi bilan bog’liq
masalalarni yechishda muhim ahamiyatga ega. Shuningdek, affine geometriyada
tekisliklar ham alohida rol o‘ynaydi. Tekisliklar bir nechta o‘zgartirishlar yordamida
o‘zgartirilsa-da, ular orasidagi o‘zaro masofalar, burchaklar va joylashuvlar affine
transformatsiyalar orqali aniq o‘lchanadi.
Metrik masalalar affine geometriyaning ajralmas qismidir. Metrik geometriya,
fazolar orasidagi masofalarni, burchaklarni va boshqa geometrik o‘lchovlarni
o‘rganadi. Affin fazolarda o‘lchovlar, ya’ni masofalar va burchaklar, affine
transformatsiyalar ta’sirida qanday o‘zgarishini aniqlash esa nazariy jihatdan juda
qiziqarli va amaliyotda zarur bo‘lgan masala hisoblanadi. Masalan, kompyuter
grafikasi sohasida ob’ektlarning o‘lchamlari va shakllarini o‘zgartirishda, fazolar
orasidagi masofalarni hisoblashda affine transformatsiyalarning qanday ta’sir
qilishini tushunish zarur.
Shu bilan birga, affine geometriya va metrik masalalar nafaqat matematik
sohada, balki amaliy sohalar, xususan, fizika, arxitektura, kompyuter fanlari va
robototexnika kabi sohalarda ham keng qo‘llaniladi. Affin transformatsiyalar
yordamida fazolarni tahlil qilish, fazolarni o‘zgartirish va yangi geometrik ob’ektlarni
yaratish imkonini beradi. Shuningdek, bu masalalar yordamida tasvirlar va
modellarni yaratishda, fazolar orasidagi masofalarni va burchaklarni aniqlashda
asosiy yondashuvlar ishlab chiqiladi.
Ushbu kurs ishida affine geometriya asosida to‘g’ri chiziqlar va tekisliklar
orasidagi masofalarni hisoblash va o‘zgartirish usullari tahlil qilinadi. Affin
transformatsiyalar yordamida geometriyadagi ob’ektlar va fazolarni qanday
o‘zgartirish mumkinligi, shuningdek, ularning metrik xususiyatlari, masofalar va
burchaklar qanday o‘zgarishini ko‘rib chiqamiz. Shuningdek, bu ishda affine
geometriya nazariyasi, uning amaliy qo‘llanilishi va metrik masalalar yuzasidan bir
qator misollarni ko‘rsatish orqali, sohaning chuqurroq o‘rganilishi maqsad qilingan.

Kurs ishining maqsadi va vazifalari: Affin fazolar haqida ma’lumot berish
va affin fazolarda to‘g’ri chiziqlar va tekisliklarning vaziyatlarini yoritib berish va
ularga oid masalar yechish ko‘rsatish.

I BOB. AFFIN FAZOLAR.
1-§. Chiziqli fazo
Fazo fundamental kattalik bo lib, quyidagicha ta riflanishi mumkin:ʻ ʼ
 olamning fundamental tuzilishi qismlaridan biri, ichida jismlar ajratilgan,
joylashgan, shakllari va hajmlari aniqlangan, harakat qilishga imkonlari
bo lgan o lchamlar to plami;
ʻ ʻ ʻ
 yuqoridagi ta rifga qarshi ma noda
ʼ ʼ : mavhum matematik konseptual soha
(vaqt va son kabi) bo lib, uning yordamida biz jismlarning joylashishi, shakli,
ʻ
hajmi, harakati va ular orasidagi masofani taqqoslaymiz va o lchaymiz;
ʻ
 Yer va uning atmosferasi tashqarisidagi koinot qismi.
Matematikada chiziqli fazo, faktor fazo, va ... lar ham bor. Biz yashab turgan
fazo 3 o lchovli fazo hisoblanadi. Va yana matematikada biz yashab turgan 3
ʻ
o lchovli fazodan tashqari 4, 5, ... o lchovli fazo tushunchalari ham kiritilgan. Albatta
ʻ ʻ
bu kiritilgan fazolar faqat nazariy jihatdan tushuntiriladi, amalda esa, hattoki, 4
o lchovli fazoni ham tasvirlab berish juda mushkul vazifa.
ʻ
Elementlari vektor deb atalgan bo‘sh bo‘lmagan V to‘plam berilgan bo‘lsin. Bu
to‘plamning elementlarini ustiga strelka qo‘yilgan kichik lotin harflari
⃗ a
, ⃗
b ,…, ⃗ x
, ⃗y
… bilan belgilaylik. Bundan tashqari, haqiqiy sonlar to‘plami R berilgan bo‘lib, V
va R elementlarini bog’lovchi ma’lum munosabatlar o‘rnatilgan bo‘lsin, jumladan:
I. V ning ixtiyoriy ikki
⃗a , ⃗b vektori uchun ularning yig’indisi deb atalgan, shu
to‘plamning elementidan iborat uchinchi bir vektor mos keltirilgan bo‘lsin, bu
vektorni
⃗a + ⃗b ko‘rinishida yozaylik.
II. V ning ixtiyoriy
⃗a vektori va ixtiyoriy k haqiqiy son uchun V ning shunday bir
elementi mos keltirilgan bo‘lsinki, bu element
⃗a vektorni k songa ko‘paytirishdan
hosil qilingan deyilib, uni k
⃗ a
ko‘rinishida yozaylik. Kiritilgan bu ikki amal quyidagi
8 ta aksiomani qanoatlantirsin.
1-aksioma: Vektorlarni qo‘shish kommutativlik qonuniga bo‘ysunadi, ya’ni

∀ ⃗a , ⃗b V ϵ uchun ⃗a + ⃗b = ⃗b + ⃗a .
2-aksioma: Vektorlarni qo‘shish guruhlanish qonuniga bo‘ysunadi, ya’ni
∀
⃗a , ⃗b,⃗c V uchun (ϵ ⃗a + ⃗b )+ ⃗c = ⃗a +( ⃗b + ⃗c ).

3-aksioma: V da nol vektor degan ⃗ 0
element mavjud bo‘lib, ∀ ⃗a V uchun ϵ
⃗
a
+ ⃗0 = ⃗ a
tenglik o‘rinli.
4-aksioma: V ning ixtiyoriy
⃗a vektori uchun V da shunday ⃗`a vektor mavjud
bo‘lib,
⃗a
+ ⃗`a = 0. Bunday ⃗`a vektor odatda ⃗a vektorga qarama-qarshi vektor deb ataladi.
 Bu to‘rtta aksioma vektorlarni qo‘shish aksiomalari deb ataladi.
5-aksioma: ∀ k
R va
ϵ ∀
⃗ a
, ⃗
b V uchun ϵ k ⃗¿¿ + ⃗
b )= k ⃗ a
+
k ⃗ b o‘rinli.
6-aksioma:
∀ k,t R va ϵ ∀ ⃗a V uchun (k+t)ϵ ⃗a = k⃗a +t ⃗a o‘rinli.
7-aksioma: ∀ k , t
R va
ϵ ∀
⃗ a
V uchun k(tϵ ⃗a¿ = (kt)⃗a o‘rinli.
8-aksioma:
∀ ⃗a V uchun ϵ 1∙⃗a = ⃗a o‘rinli.
 Bu to‘rtta aksioma vektorni songa ko‘paytirish aksiomalari deb ataladi.
Shu sakkizta aksioma shartlarini qanoatlantiruvchi V to‘plam chiziqli fazo yoki
vektor fazo deyiladi.
Bundan keyin biz chiziqli fazo elementlarini vektorlar deb aytamiz. Agar
chiziqli fazodagi vektorlar uchun faqat haqiqiy songa ko‘paytirish amali aniqlangan
bo‘lsa, u holda bunday fazo haqiqiy chiziqli fazo deyiladi. Agar chiziqli fazodagi
vektorlar uchun kompleks songa ko‘paytirish amali aniqlangan bo‘lsa, u holda
bunday fazoga kompleks chiziqli fazo deyiladi.
9-aksioma: V vektor fazoda n ta chiziqli erkli vektor mavjud
10-aksioma: V vektor fazodagi har qanday n+1 ta vektorlar sistemasi chiziqli
bog’liqdir.
Keltirilgan 10 ta aksioma shartlarini qanoatlantiruvchi vektor fazo n o‘lchovli
vektor fazo deyiladi va u
Vn bilan belgilanadi.
Chiziqli fazoni aniqlovchi aksiomalardan, quyidagi xossalarni ajratish uchun:
1-xossa. Har qanday chiziqli fazo uchun yagona
⃗θ vektor mavjud.
2-xossa . Har qanday chiziqli fazoda har bir
⃗ x
vektor uchun unga qarama-qarshi
bo‘lgan yagona ( −
⃗ x )
vektor mavjud.
3-xossa. Har qanday chiziqli fazoda har bir
⃗ x
vektor uchun ⃗
θ ∙ ⃗ x = ⃗ θ tenglik o‘rinli.

4-xossa. Har qanday λ haqiqiy son va ⃗θ ∈ V element uchun λ ∙⃗θ= ⃗θ munosabat hamma
vaqt bajariladi.
5-xossa. λ
∙⃗a=⃗θ ⟹ bunda λ=0 yoki ⃗a= ⃗θ .
Izoh. ⃗ y −
⃗ x
vektorlar ayirmasi deb, ⃗yva (−⃗x) vektorlar yig’indisi tushuniladi.
1.1.1-Ta’rif : V chiziqli fazodan olingan x
1 , x
2 , … x
n elementlar
λiRϵ , (i=1,2,3,
…n) sonlar yordamida qurilgan
λ1 x
1 + λ
2 x
2 + λ
3 x
3 + … + λ
n x
n ifodaga x
1 , x
2 , … x
n
elementlarning chiziqli kombinatsiyasi deyiladi.
1.1.2-Ta’rif : Agar y = λ
1 x
1 + λ
2 x
2 + λ
3 x
3 + … + λ
n x
n tenglik o‘rinli bo‘lsa, u
holda y element x
1 , x
2 , … x
n elementlarning chiziqli kombinatsiyasidan iborat
deyiladi.
1.1.3-Ta’rif : Agar λ
1 , λ
2 , … λ
n koeffitsiyentlardan hech bo‘lmaganda bittasi
noldan farqli bo‘lganda
λ1 x
1 + λ
2 x
2 + λ
3 x
3 + … + λ
n x
n =θ tenglik o‘rinli bo‘lsa, u
holda x
1 , x
2 , … x
n elementlar chiziqli bog’liq deyiladi.
Agar
λ1 x
1 + λ
2 x
2 + λ
3 x
3 + … + λ
n x
n =θ tenglik λ
1 , λ
2 , … λ
n koeffitsiyentlardan
barchasi nolga teng bo‘lgandagina o‘rinli bo‘lsa, u holda x
1 , x
2 , … x
n elementlar
chiziqli erkli, aks holda x
1 , x
2 , … x
n elementlar chiziqli bog’liqli deyiladi. Bu yerda, θ
chiziqli fazoning nol elementi.
1.1.4-Ta’rif : Agar V chiziqli fazoda n ta chiziqli erkli elementlar mavjud
bo‘lib, har qanday n+1 ta element chiziqli bog’liqli bo‘lsa, u holda V chiziqli
fazoning o‘lchovi n ga teng deyiladi.
1.1.5-Ta’rif : n o‘lchovli V chiziqli fazoda har qanday n ta chiziqli erkli
vektorlar sistemasi bu fazoning bazisi deyiladi.
Odatda bazis vektorlar sistemasi
⃗e1,⃗e2,... ,⃗en
kabi belgilanadi. Masalan, darajasi n dan
oshmaydigan barcha ko‘phadlar to‘plami chekli o‘lchovli, ya’ni (n+1) o‘lchovli
chiziqli fazo tashkil qiladi. Bu fazoning bazisini { 1, t, t 2
, …,
t n
}
vektorlar sistemasi
tashkil qiladi.
2-§. n o‘lchovli affin fazo. Affin koordinatalar sistemasi .
n o‘lchovli affin fazo

n o‘lchovli vektor fazo va elementlari nuqtalar deb atalgan (bu elementlarni biz bosh
lotin harflari bilan belgilaymiz) Ω
={ A , B , ... }
to‘plam berilgan bo‘lsin. Ω
to‘plam bilan
Vn
to‘plam orasida shunday moslik o‘rnatamizki, Ω dan ma’lum tartibda olingan ikki
M, N nuqtalar uchun V
n dagi aniq bitta
⃗a vektor mos kelsin, buni ⃗a=⃗MN deb
belgilaymiz. Lekin shuni ta’kidlash zarurki,
Vn dagi har bir vektorga Ω da
nuqtalarning tartiblangan turli juftlari mos kelishi mumkin. Masalan,
⃗ a
= ⃗MN = ⃗ PQ
= ⃗KL ,
bunda M, N, P, Q, K, L larning barchasi
Ω ga tegishlidir.
⃗a=⃗MN
yozuvini quyidagicha ifodalaymiz: ⃗ a
vektorni M nuqtadan qo‘yish bilan N
nuqta hosil qilinadi.
Yuqorida keltirilgan Ω
bilan V
n orasidagi moslikning quyidagi ikki aksiomani
qanoatlantirishi talab qilinadi.
11-aksioma: ∀ M

ϵΩ va ∀
⃗ a
ϵ V
n uchun yagona shunday N ϵΩ mavjudki,
uning uchun
⃗ a = ⃗ MN
.
12-aksioma:
∀ ⃗ A
, ⃗ B , ⃗ C
ϵΩ uchun ⃗ AB
+ ⃗ BC
= ⃗AC .
 Bu ikkita aksioma ba’zan vektorni nuqtadan boshlab qo‘yish aksiomalari deb
yuritiladi.
1.2.1-Ta’rif: Elementlari yuqoridagi barcha 12 ta aksiomalarni
qanoatlantiruvchi bo‘sh bo‘lmagan to‘plam n o‘lchovli affin fazo deb ataladi. Uni
An
orqali belgilaymiz. Agar V
n vektor fazo kompleks vektor fazo bo‘lsa, u holda A
n ham
kompleks affin fazo deb ataladi.
Demak, n o‘lchovli affin fazoni simvolik ravishda quyidagi ko‘rinishda yozish
mumkin ekan:
An = Vn ∪ Ω
V
n vektor fazo A
n affin fazoning eltuvchisi deyiladi.
Xususiy holda, n=1 bo‘lsa,
A1 bir o‘lchovli affin fazo bo‘lib, V1 ning element-
larini odatdagi geometrik vektorlar deb olsak, affin to‘g’ri chiziq hosil bo‘ladi. Agar
n=2 bo‘lsa, affin tekislik hosil bo‘ladi.
Affin koordinatalar sistemasi.
Koordinatalar sistemasi tekislikda qanday kiritilgan bo‘lsa, fazoda ham shu
usulda kiritiladi. Aniqrog’i, koordinatalarning affin sistemasi (affin reper) biror O

nuqta va shu nuqtadan qo‘yilgan ma’lum tartibda olingan uchta nokomplanar ⃗e1 , ⃗e2,⃗e3
vektorlar sistemasidan iborat, bu sistemani B( O,
⃗ e
1 , ⃗e2,⃗e3 ) ko‘rinishida belgilaymiz.
O nuqtadan o‘tib,
⃗e1 , ⃗e2,⃗e3 vektorlar bilan aniqlanadigan to‘g’ri chiziqlar mos ravishda
Ox, Oy, Oz deb belgilab, ular koordinata o‘qlari, birinchisi absissalar o‘qi, ikkinchisi
ordinatalar o‘qi va, nihoyat, uchinchisi applikatalar o‘qi deb ataladi. Bu o‘qlarning
har ikkitasi bilan aniqlanadigan uchta tekislik xOy, xOz, yOz deb belgilab, ular
koordinata tekisliklari deb ataladi.
Quyidagi chizmada affin koordinatalar sistemasi va xOy, xOz, yOz tekisliklar
ham ko‘rsatilgan:
B sistema berilganda, fazodagi har bir M nuqtaga aniq bir
⃗ OM
vektorni doimo
mos keltirish mumkin, ya’ni boshi koordinatalar boshida, oxiri esa berilgan M
nuqtada bo‘lgan vektorni mos keltiriladi.
⃗
OM vektorning koordinatalari (x, y, z) bo‘lsa, u holda bu uchta x, y, z son M
nuqtaning affin reperdagi koordinatalari bo‘ladi:
⃗OM
(x, y, z) ⟺ M(x, y, z) (1.2.1)
Demak, fazo nuqtalari to‘plami bilan ma’lum tartibda olingan haqiqiy sonlar
uchliklari to‘plami orasida biektiv moslik mavjud.

Berilgan nuqtaning koordinatalarini topish uchun shu nuqta radius-vektori-ning
koordinatalarini topish kifoya va aksincha. Masalan quyidagi keltirilgan chizmada
koordianatalari (2; 3; 2) bo‘lgan nuqtani yasash usuli ko‘rsatilgan.
Umuman M(a, b, c) nuqtani yasash uchun, ya’ni ⃗OM = a⃗e1 + b⃗e2+⃗ce 3 (1.2.2)
vektorning oxirini topish uchun quyidagi qoidadan foydalaniladi koordinatalar
boshidan Ox o‘qi bo‘yicha
a⃗e1 vektor, uning oxiridan Oy o‘qqa parallel holda b⃗e2
vektor qo‘yiladi, so‘ngra uning oxiridan c
⃗ e
3 vektor yasalsa, shu vektorning oxiri
izlangan nuqta bo‘ladi.
Uchta koordinata tekisligi birgalikda fazoni sakkiz qismga ajratadi, ularning
har biri oktantalar deb ataladi.
Kesmani berilgan nisbatda bo‘lish
Biror affin reperda M
1 ( x
1 , y
1 , z
1 ), M
2 (x
2 , y
2 , z
2 ) (M
1 ≠M
2 ) nuqtalar va biror
haqiqiy λ (λ≠-1) son berilgan bo‘lsin.
1.2.2-Ta’rif : M nuqta uchun
⃗ M
1 M
=λ ⃗MM 2 (1.2.3) shart bajarilsa, M nuqta
M
1 M
2 kesmani λ nisbatda bo‘ladi deyiladi.
M
1 , M
2 nuqtalarning koordinatalari orqali M nuqtaning x, y, z koordinatalarini
topaylik. (1.2.2) ga asosan
⃗
M
1 M =OM-OM
1 = (x-x
1 ) ⃗e1 +(y-y
1 ) ⃗e2 +(z − z
1 )
⃗e3 ,
⃗M 1M
(x-x
1 ,y-y
1 , z
− z 1 )
.
⃗M 2M
=OM
2 -OM=( x
2 -x ) ⃗ e
1 +(y
2 -y) ⃗e2 +(z
2 − z )
⃗e3 ,

⃗M M 2 = (x
2 -x , y
2 -y , z
2 -z )
.
Bu ifodalarni (3) ga qo‘yib va
⃗ e
1 , ⃗e2,⃗e3 ning chiziqli erkliligini e’tiborga olsak,
x-x
1 =λ (x
2 -x) , y-y
1 = λ(y
2 -y) , z
− z
1 = λ (z
2 -z) .
Bulardan
x= x
1 + λ x
2
1 + λ , y= y
1 + λ y
2
1 + λ , z= z
1 + λ z
2
1 + λ (1.2.4)
Berilgan kesmani berilgan nisbatda bo‘luvchi nuqtaning koordinatalarini
topish formulalari shulardir. M nuqta M
1 M
2 kesmaning o‘rtasi bo‘lsa, (1.2.4) formula
quyidagi ko‘rinishni oladi:
x= x
1 + x
2
2 , y= y
1 + y
2
2 , z= z
1 + z
2
2 (1.2.5)
Bu formulalar kesma o‘rtasining koordinatalarini topish formulalaridir.
To‘g’ri burchakli dekart koordinatalar sistemasi
Affin sistemaning xususiy hollaridan biri to‘g’ri burchakli dekart koordinatalar
sistemasidir.
Affin sistemadagi bazis vektorlar ortonormalangan bo‘lsa, ya’ni ularning har
ikkitasi o‘zaro perpendikulyar bo‘lib, har biri birlik vektor bo‘lsa, (O,
⃗i , ⃗j , ⃗
k ) dekart
reperi hosil qilinadi, bu yerda
⃗
i 2
= ⃗
j 2
= ⃗
k 2
= 1 (1.2.6)
⃗
i
⃗ j
= ⃗j ⃗k = ⃗ i
⃗k = 0 (1.2.7)
Bu reperda metrik harakterdagi masalalarni yechish ancha qulay ,
a)
⃗a = (x
1 , y
1 , z
1 ) vektorning uzunligini hisoblaylik. Vektorning uzunligi quyidagi
formula orqali hisoblanadi:

|⃗ a|
= √x12+y12+z12 (1.2.8)
b)
⃗a = ( x
1 , y
1 , z
1 ) va ⃗b = (x
2 , y
2 , z
2 ) vektorlarning skalyar ko‘paytmasi quyidagi
formula orqali hisoblanadi:
⃗a
⃗b = x
1 x
2 + y
1 y
2 + z
1 z
2 (1.2.9)
c) Yuqoridagi ikki vektor orasidagi burchakning kosinusi formulasi esa:

cos φ = ¿⃗ a⃗ b
|⃗
a⃗ b| ¿
=
x1x2+y1y2+z1z2
√x12+y12+z12√x22+y22+z22 (1.2.10)
d)
⃗ M
1 = (x
1 , y
1 , z
1 ) va ⃗ M
2 = (x
2 , y
2 , z
2 ) nuqtalar berilgan bo‘lsa, ular orasidagi
ρ (M
1, M
2 )
=
⃗ M M
2 masofani topish mumkin:
ρ (M
1, M
2 )
=
√(x2− x1)2+(y2− y1)2+(z2− z1)2 (1.2.11)
Misol: B(O,
⃗e1 , ⃗e2,⃗e3 ) reperda uchlari A(7, 2, 4), B(4, -4, 2), C(6, -7, 8) va D(9, -1,
10) nuqtalarda bo‘lgan to‘rtburchakning kvadrat ekanligini isbotlang.
Yechish:Avvalo,
⃗ AB , ⃗ DC
vektorlarning koordinatalarini topaylik:
⃗
AB (-3, -6, -2) va ⃗DC (-3, -6, -2) .
Bulardan ko‘rinadiki,
⃗ AB
= ⃗ DC
, demak, ABCD to‘rtburchak parallelogramm ekan,
uning kvadrat ekanini ko‘rsatish uchun dioganallari o‘zaro teng perpendikulyar
ekanligini isbotlash kerak(chizmada berilgan).
Haqiqatan ham, ρ(A, C) va ρ(D, B) larni (1.2.11) formula bo‘yicha hisoblasak,

ρ(A, C)=√(6−7)2+(−7− 2)2+(8− 4)2 = √ 1 + 81 + 16 = √ 98
,
ρ(D, B)=
√(4− 9)2+(− 4+1)2+(2−10 )2 = √ 25 + 9 + 64 = √ 98
,
bundan ρ(A, C)=ρ(D, B) ekanligi ko‘rinib turibdi.
⃗AC
(-1, -9, 4), ⃗
DB (-5, -3, -8) bo‘lgani uchun (1.2.9) ga asosan:
⃗
AC ∙ ⃗ DB =(-1)(-5)+(-9)(-3)+4(-8)=5+27–32=0
Demak,
⃗ AC ⊥ ⃗ DB
.
3-§. n o‘lchovli affin fazolarning izomorfligi.
Avvalo, ikki vektor fazoning izomorfligi tushunchasiga ta’rif beramiz:
Faraz qilaylik, V va V` vektor fazolar berilgan bo‘lsin.
1.3.1- Ta’rif: V ⟶ V` akslantirish o‘zaro bir qiymatli bo‘lib, quyidagi ikki
shartni qanoatlantirsa, u chiziqli izomorf akslantirish deb ataladi:
I.
∀ ⃗a , ⃗b V uchun φ(ϵ ⃗a + ⃗b¿ = φ(⃗a) +
φ ⃗ ( b ¿ ) ¿ bo‘lsa, ya’ni V dagi ikki ixtiyoriy vektor
yig’indisiga V` da shu vektorlarga mos kelgan vektorlarning yig’indisi mos kelsin.
II.
∀ ⃗a V uchun va ϵ ∀ λ R ϵ uchun φ( λ ⃗ a
)=λφ( ⃗ a ¿
bo‘lsa, ya’ni V dagi ⃗ a
vektorni biror
λ songa ko‘paytirishdan hosil bo‘lgan vektorning obrazi
⃗a va V’ dan mos kelgan
vektorning λ songa ko‘paytirishdan hosil bo‘lgan vektordan iborat bo‘lsin.
Bu ta’rifdan quyidagi natija kelib chiqadi: V bilan V` izomorf bo‘lsa, V
dagi chiziqli erkli vektorlarga V` da mos bo‘lgan vektorlar ham chiziqli erkli bo‘ladi,
xususiy holda V ning nol vektoriga V` ning ham nol vektori mos keladi.
1.3.1- Teorema: Ikki vektor fazoning izomorf bo‘lishi uchun ularning
o‘lchovlari teng bo‘lishi zarur va yetarlidir.
Isbot: Yetarliligi. V, V` vektor fazolarning o‘lchovlari bir xil bo‘lsin, ya’ni V=V
n ,
V`=V
n `
. Bu fazolarning izomorf ekanligini isbotlaymiz. V
n ning bazisi B= (
⃗e1,⃗e2,... ,⃗en
) , V`
n ning bazisi B`=(
⃗e1,⃗e2,... ,⃗en ) bo‘lsin. ∀ ⃗a V ϵ
n bo‘lsa, u holda ⃗a ning B
bazisdagi koordinatalarini x
1 , x
2 , … x
n deylik:
⃗
a
=x
1 ⃗ e
1 + x
2 ⃗e2 +…+ x
n ⃗ e
n
Shu
⃗a vektorga V`
n da shunda y⃗a vektorni mos keltiramizki, uning B` dagi
koordinatalari x
1 , x
2 , … x
n bo‘lsin, bu moslikni φ deb belgilaylik, u holda
⃗a
= x
1 ⃗e1 + x
2 ⃗e2 +…+ x
n ⃗en

Topilgan bu φ mosligimiz o‘zaro bir qiymatlidir, chunki har bir vektor yagona
usulda bazis vektorlar bo‘yicha ifodalanadi. Endi yuqoridagi ikki shartning
bajarilishini tekshiramiz.∀
⃗a , ⃗ b
Vϵ
n ⟹ ⃗ a
= x
1 ⃗ e
1 + x
2 ⃗e2 +…+ x
n ⃗ e
n
⃗b
= y
1 ⃗e1 + y
2 ⃗e2 +…+ y
n ⃗en
bu vektorlarga V`
n da mos kelgan
φ(⃗a)=⃗a ,
φ ⃗ ( b ¿ ) = ⃗ b ¿ vektorlar B` da quyidagicha
yoyilmaga ega bo‘ladi:
⃗
a
= x
1 ⃗ e
1 + x
2 ⃗ e
2 +…+ x
n ⃗en va ⃗
b = y
1 ⃗ e
1 + y
2 ⃗e2 +…+ y
n ⃗ e
n
U holda
⃗a + ⃗b = (x
1 +y
1 ) ⃗e1 + (x
2 +y
2 ) ⃗e2 +…+ (x
n +y n )
⃗en va
⃗
a
+ ⃗
b = φ(⃗a)+φ(⃗b) = (x
1 +y
1 ) ⃗ e
1 + (x
2 +y
2 ) ⃗ e
2 +…+ (x
n + y
n )
⃗en = φ ( ⃗ a + ⃗ b )
.
Demak, birinchi shart bajarildi.
Endi ikkinchi shartini bajarilishini tekshiraylik. ∀
λ R ni olsak,
ϵ
⃗λa
= λx
1 ⃗e1 + λx
2 ⃗e2 +…+ λx
n ⃗en ,
λφ (
⃗ a )
= λ ⃗a = λ ( x
1 ⃗ e
1 + x
2 ⃗ e
2 +…+ x
n ⃗en )=
= λx
1
⃗e1 + λx
2 ⃗e2 +…+ λx
n ⃗en = φ ( λ ⃗ a )
.
Demak, V, V` izomorf.
Zaruriyligi. ξ:V ⟶ V` akslantirish izomorf moslikdan iborat bo‘lsa, ularning
o‘lchovlari teng ekanligini ko‘rsataylik. Faraz qilaylik, V=V
n , V`=V
m `
bo‘lib,
aniqlik uchun m<n bo‘lsin. V
n ning o‘lchovi n bo‘lgani uchun unda n ta chiziqli erkli
vektor mavjuddir, yuqoridagi natijaga asosan shu vektorlarning obrazlari ham chiziqli
erkli bo‘ladi, demak, V
m ning ham o‘lchovi ham n bo‘lishi kerak, bundan n=m kelib
chiqadi.
Xullas, bir xil o‘lchovli barcha vektor fazolar o‘zaro izomorfdir, ya’ni biror
vektor fazoga taalluqli da’vo (yoki tasdiq) shu fazoga izomorf barcha fazolar uchun
ham o‘rinli bo‘ladi.
1.3.2- Ta’rif: Eltuvchi vektor fazolari o‘zaro izomorf bo‘lgan ikki affin fazo
izomorf deb ataladi.

Bu ta’rifdan ko‘rinadiki, ikki affin fazo o‘zaro izomorf bo‘lishi uchun ular bir
xil o‘lchovli bo‘lishi zarur va yetarlidir. Bundan esa bir xil o‘lchovli barcha affin
fazolarning o‘zaro izomorfligi kelib chiqadi.

I I BOB. AFFIN FAZOLARDA TO‘G’RI CHIZIQ VA TEKISLIK.
1-§. Affin fazolarda tekislik.
Fazodagi eng sodda sirtlardan biri tekislikdir. Nuqta va to‘g’ri chiziq bilan bir
qatorda tekislik geometriyaning ta’riflanmaydigan asosiy tushunchalaridan
hisoblanadi. Biz tekislikning fazodagi vaziyatini to‘liq aniqlovchi ba’zi miqdorlar
yordamida uning turli ko‘rinishli tenglamalari bilan ish ko‘rib, tekislikka oid bir qator
masalalarni qarab chiqamiz. Fazodagi to‘g’ri chiziq esa ikki tekislikning kesishgan
chizig’i deb qaraladi.
1. Nokolleniar ikki ⃗p1,⃗p2 vektor va bitta M 0 nuqta P tekislikning vaziyatini to‘la
aniqlaydi.
∀ M ∈ P nuqtani olaylik. U holda
⃗M 0M vektor ⃗p1,⃗p2 vektorlar bilan komplanar
bo‘ladi, demak, bu vektorlar chiziqli bog’liq bo‘lib, bundan ularning koordinatalridan
tuzilgan uchinchi tartibli determinant nolga teng bo‘lishi kelib chiqadi.
2.1.1-rasm.
Shuni koordinatalarini yozaylik:
M
0 (x
0 , y
0 , z
0 ) ,
⃗ p
1 (a
1 , b
1 , c
1 ) , ⃗ p
2 (a
2 , b
2 , c
2 ) (2.1.1)
bo‘lsin. M ning koordinatalarini x, y, z deb belgilasak,
⃗ M
0 M
( x–x
0 , y–y
0 , z–z
0 ) bo‘lib,
quyidagi tenglama hosil bo‘ladi:
|
x− x0 y− y0 z− z0
a1 b1 c1
a2 b2 c2 |
=0 (2.1.2)
Aksincha, (2.1.2) shart bajarilsa, M nuqta, albatta, P tekislikka tegishli bo‘ladi.
Demak, (2.1.2) P tekislikning tenglamasi. Bu tenglama berilgan nuqtadan o‘tib,
berilgan ikki vektorga parallel bo‘lgan tekislikning tenglamasi deb yuritiladi.
M 0 P

Bundan tashqari, ⃗M 0M , ⃗p1,⃗p2 vektorlar bir tekislikda yotgani uchun ular chiziqli
bog’liqdir, ya’ni
⃗M 0M
= u ⃗ p
1 + v ⃗ p
2 , u, v ∈ R, (2.1.3)
bu yerda u, v sonlar parametrlardir. (2.1.3) dan
x – x
0 = ua
1 + va
2 x = a
1 u + a
2 v + x
0
y – y
0 = ub
1 + vb
2 ⟹ y = b
1 u + b
2 v + y
0 (2.1.4)
z – z
0 = uc
1 + vc
2 z=c
1 u + c
2 v + z
0
(2.1.4) tekislikning parametrik tenglamalari deb ataladi( u va v ga istalgan qiymatlar
berib, tekislikning shu parametrlarga mos nuqtalarini topish mumkin).
Endi (2.1.2) tenglamani quyidagicha yozaylik:
A(x–x
0 )+B(y–y
0 )+C(z–z
0 )=0 (2.1.5)
Bundan esa
A =
| b
1 c
1
b
2 c
2 | , B= | c
1 a
1
c
2 a
2 | , A= | a
1 b
1
a
2 b
2 | (2.1.6)
(2.1.5) ⟹ Ax+By+Cz- (Ax
0 +By
0 +Cz
0 ) =0 bunda, (Ax
0 +By
0 +Cz
0 )=D
desak,
Ax+By+Cz+D=0 (2.1.7)
tenglama hosil bo‘ladi. (2.1.2) ⟺ (2.1.7) bo‘lgani uchun (2.1.7) ham tekislikning
tenglamasidir. (2.1.6) da A, B, C larning kamida bittasi noldan farqli (A 2
+B 2
+C 2
≠0) ,
aks holda A=B=C=0 bo‘lsa, (2.1.6) dan a
1 =λa
2 , b
1 =λb
2 , c
1 =λc
2 ⟹
⃗ p
1 ∥ ⃗ p
2 ,
bu esa ⃗ p
1 , ⃗ p
2
larning berilishiga zid. Shunday qilib, tekislik affin reperda (2.1.7) chiziqli tenglama
bilan ifodalanadi. Bu xulosaning teskarisi ham o‘rinlidir, ya’ni (2.1.7) ko‘rinishdagi
har qanday chiziqli tenglama fazodagi biror affin reperga nisbatan tekislikni
aniqlaydi.
Haqiqatan, Ax+By+Cz=0 (A 2
+B 2
+C 2
≠0) tenglama biror afffin reperda biror
nuqtalar to‘plamini aniqlasin. Uch o‘zgaruvchisini bog’lagan bu tenglamaning
yechimi cheksiz ko‘pdir, ularning biri (x
0 ,y
0 ,z
0 ) bo‘lsa, u holda Ax
0 +By
0 +Cz
0 =0,
bundan va (2.1.7) dan ⇒ A(x–x
0 )+B(y–y
0 )+C(z–z
0 )=0 ⟶ tekislik tenglamasidir.
(2.1.7) tenglama tekislikning umumiy tenglamasi deb ataladi.

2. Bir to‘g’ri chiziqda yotmagan uchta nuqta tekislikning vaziyatini to‘la aniqlaydi.
Shu ma’lumotlarga ko‘ra uning tenglamasini tuzaylik. Berilgan nuqtalar M
1 (x
1 ,y
1 ,z
1 ),
M
2 (x
2 ,y
2 ,z
2 ), M
3 (x
3 ,y
3 ,z
3 ) bo‘lsin. Biz M
0 =M, ⃗p1=⃗M 1M 2,⃗p2=⃗M 1M 3 desak, hamda
⃗M 1M 2
(x
2 –x
1 , y
2 –y
1 , z
2 –z
1 ) , ⃗M 1M 3 (x
3 –x
1 , y
3 –y
1 , z
3 –z
1 ) ni e’tiborga olsak, (2.1.2)
tenglama quyidagi ko‘rinishni oladi:
|
x− x1 y− y1 z− z1
x2− x1 y2− y1 z2− z1
x3− x1 y3− y1 z3− z1|
=0 (2.1.8)
Uch nuqtadan o‘tgan tekislikning tenglamasi shudir.
Agar tekislik koordinatalar boshidan o‘tmasa, u Ox,Oy, Oz o‘qlarni uchta
M
1 (a, 0, 0), M
2 (0, b, 0),M
3 (0, 0, c) nuqtada kesadi, bu yerda a, b, c tekislikning shu
o‘qlardan ajratgan kesmalaridir. Bunga (2.1.8) ko‘rinishli tenglamani tatbiq qilamiz:
|
x−a y z
−a b 0
−a 0 c|
=0
bundan
x
a + y
b + z
c = 1
(2.1.9)
bu tenglama tekislikning koordinata o‘qlaridan ajratgan kesmalari bo‘yicha
tenglamasi deb ataladi.
Misol. Tekislik A(2, 0, 3) nuqtadan o‘tib,
⃗ p
1 (1, 0, 1) , ⃗ p
2 (2, 1, 3) vektorlarga parallel
bo‘lsin. Shu tekislikning parametrik va umumiy tenglamasini tuzing.
Yechish. Berilganlarni (2.1.4) ko‘rinishdagi parametrik tenglama bilan solishtirsak,
x
0 =2, y
0 =0, z
0 =3, a
1 =1, b
1 =0, c
1 =1, a
2 =2, b
2 =1, c
2 =3; bularni (2.1.4) ga qo‘yamiz:
x=u+2v+2, y=v, z=u+3v+3.
Endi tekislikning (2.1.2) ko‘rinishdagi tenglamasini yozaylik:
|
x−2 y−0 z− 3
1 0 1
2 1 3 |
=0.
Bundan, (z–3)+2y–(x–2)–3y=0 yoki x+y–z+1=0.
Endi ba’zi xususiy hollarni ko‘rib chiqaylik.

1) D=0 ⟹ Ax+By+Cz=0 ko‘rinishni oladi va bu tekislik koordinatalar boshidan
o‘tadi. (1-a chizma)
2) C=0 ⟹ Ax+By+D=0 ko‘rinishni oladi va bu tekislik ⃗e3 (0, 0, 1) vektorga parallel
bo‘ladi, demak, Oz o‘qqa ham parallel. (1-b chizma)
Shunga o‘xshash (2.1.7) da B=0(yoki A=0) bo‘lsa, tekislik Oy o‘qqa (yoki Ox
o‘qqa) paralleldir. Bundan quyidagi umumiy xulosa kelib chiqadi: tekislikning
umumiy tenglamasida qaysi o‘zgaruvchi qatnashmasa, bu tenglama bilan
aniqlanadigan tekislik shu o‘zgaruvchi bilan bir ismli koordinatalar o‘qiga paralleldir.
3) C=D=0 ⇒ Ax+By=0, O ∈ P va P ∥ Oz ⟹ ushbu tekislik Oz o‘qdan o‘tadi. (1-c
chizma).
Eslatma. Agar tekislik tenglamasi berilib, uning biror reperdagi tasvirini chizish talab
qilinsa, umumiy holda quyidagicha ish ko‘riladi: tenglamada uch noma’lum bo‘lgani
uchun ulardan ikkitasiga ixtiyoriy qiymatlar berish bilan uning cheksiz ko‘p
yechimlarini topish mumkin. Shu yechimlardan ixtiyoriy uchtasini olib,
koordinatalari shu sonlardan iborat (bu uch nuqta bir to‘g’ri chiziqda yotmaydigan
qilib olinadi) uchta nuqta yasaymiz.
Tekislik tasvirini chizishda ko‘pincha uning koordinata o‘qlari bilan kesishgan
nuqtalarini topish qulaydir, buning uchun o‘zgaruvchilarning ikkitasiga nol qiymat
berib, uchinchi o‘zgaruvchini berilgan tenglamadan topiladi(D≠0 shartda)
Dekart reperida tekislikka doir ba’zi masalalar
Dekart reperi affin reperning xususiy holi bo‘lgani uchun affin reperida
chiqarilgan tenglamalar dekart reperida ham o‘z kuchini saqlaydi, lekin dekart
reperida tekislikka doir metrik xarakterli masalalarni yechish mumkin.

1. Ax + By + Cz + D = 0 tenglama affin reperda tekislikning umumiy tenglamasidir,
shu tenglamani dekart reperida qarasak, A, B, C parametrlarning muhim geometrik
xossasi ayon bo‘ladi.
Haqiqatan, berilgan tenglamaga ekvivalent bo‘lgan ushbu tenglamani olaylik:
A(x–x
0 )+B(y–y
0 )+C(z–z
0 )=0 .
Endi ⃗ n
(A, B, C) va ⃗M M 0 (x-x
0 , y-y
0 , z-z
0 ) deb olinsa, oxirgi tenglikning chap
tomoni
⃗ n
va ⃗M M 0 vektorlarning skalyar ko‘paytmasini ifoda qiladi. Demak, ⃗ n
⃗M M 0
0 ⇒
⃗ n
⊥ ⃗M M 0 ?????? P ⟹ ⃗ n
⊥ P.
Xullas , A, B, C sonlar berilgan tekislikka perpendikulyar vektorni aniqlaydi. Shu
vektor tekislikning normal vektori deb ataladi. Biz
A(x–x
0 )+B(y–y
0 )+C(z–z
0 )=0 (2.1.10)
(2.1.11) tenglamani berilgan M
0 (x
0 , y
0 , z
0 ) nuqtadan o‘tib, berilgan
⃗ n
(A, B, C)
vektorga perpendikulyar tekislikning tenglamasi deb atashga haqlimiz.
2. Endi berilgan nuqtadan berilgan tekislikkacha bo‘lgan masofani topish masalasini
qaraylik.
Ta’rif. Berilgan M
1 nuqtadan berilgan P tekislikkacha bo‘lgan masofa deb, shu
nuqtadan tekislikka tushirilgan perpendikulyar to‘g’ri chiziqning tekislikning
kesishgan nuqtasi orasidagi masofaga aytiladi.
P tekislik umumiy tenglamasi bilan berilgan bo‘lib, M
1 (x
1 , y
1 , z
1 ) ∉ P bo‘lsin. M
1 dan P
ga perpendikulyar tushirib, uning asosini M
0 (x
0 , y
0 , z
0 ) desak, M
0 ∈ P bo‘lgani uchun
Ax
0 +By
0 +Cz
0 +D=0 ` (2.1.11)
U holda
⃗ n
(A, B, C) vektor P ning normal vektoridir.
⃗n
∥ ⃗M M 0 , demak:
⃗M 0M 1∙⃗n=¿
|⃗ M
0 M
1 | ∙ |⃗ n|
cos ( ⃗M 0M 1⃗n ) = ρ (M
1 , P) ∙ ⃗ n
,
bundan,
ρ(M
1 ,P)=
|⃗ M
0 M
1 | ∙|⃗ n|
|⃗
n| (2.1.12)
⃗
M
0 M
1 (x
1 – x
0 , y
1 – y
0 , z
1 – z
0 ); (2.1.12) dan

ρ (M
1 , P)= ¿ ¿
=|Ax1+B y1+C z1−(Ax0+B y0+C z0)|
√A2+B2+C2 (2.1.13)
(2.1.11) ga asosan
ρ (M
1 , P) =
| A x
1 + B y
1 + C z
1 + D |
√
A 2
+ B 2
+ C 2 (2.1.14)
Bu biz izlagan formuladir.
Tekisliklarning o‘zaro vaziyati
1. Ikki tekislikning o‘zaro vaziyati. Biror B(O,
⃗ e
1 , ⃗ e
2 , ⃗ e
3 ) affin reperga nisbatan P
1 , P
2
tekisliklar umumiy tenglamalari bilan berilgan bo‘lsin:
P
1 : A
1 x + B
1 y + C
1 z + D
1 = 0
P
2 : A
2 x + B
2 y + C
2 z + D
2 = 0 (2.1.15)
Ikki tekislik yo to‘g’ri chiziq orqali kesishadi, yoki ular o‘zaro parallel bo‘lib,
umumiy nuqtaga ega emas, yoki ustma-ust tushadi. Bu holning qay biri yuz berishini
bilish uchun P
1 , P
2 ga tegishli tenglamalar sistemasini tekshiramiz. Avvalo , quyidagi
matritsalarni tuzib olamiz:
M=
( A
1 B
1 C
1
A
2 B
2 C
2 ) , M *
= ( A
1 B
1 C
1 D
1
A
2 B
2 C
2 D
2 )
M matritsaning rangini r, kengaytirilgan M *
matritsaning rangini r *
deb belgilaylik.
Bu yerda quyidagi hollar bo‘lishi mumkin.
1) P
1 , P
2 tekisliklar ustma-ust tushsa, ularning tenglamalarida
A
1 = λA
2 , B
1 =λB
2 , C
1 = λC
2 , D
1 = λD
2 , ya’ni r = r *
= 1
(2.1.16)
Aksincha, (2.1.11) shartlar o‘rinli bo‘lsa, (2.1.10) tenglamalar ekvivalent bo‘lib,
P
1 =P
2 , demak, P
1 = P
2 ⇐⇒ r = r *
=1 (2-a rasm )
2) P
1 ,P
2 lar har xil, lekin parallel bo‘lsa, u holda (16) shartlardan birinchi uchtasi
bajariladi, lekin D
1 ≠ λD
2 (2-b rasm ), bu vaqtda r *
=2, r = 1.

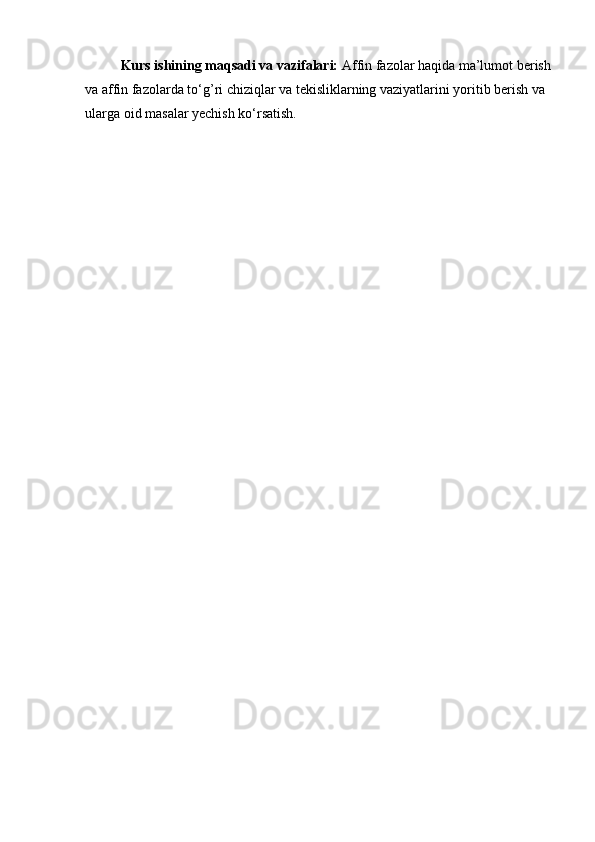
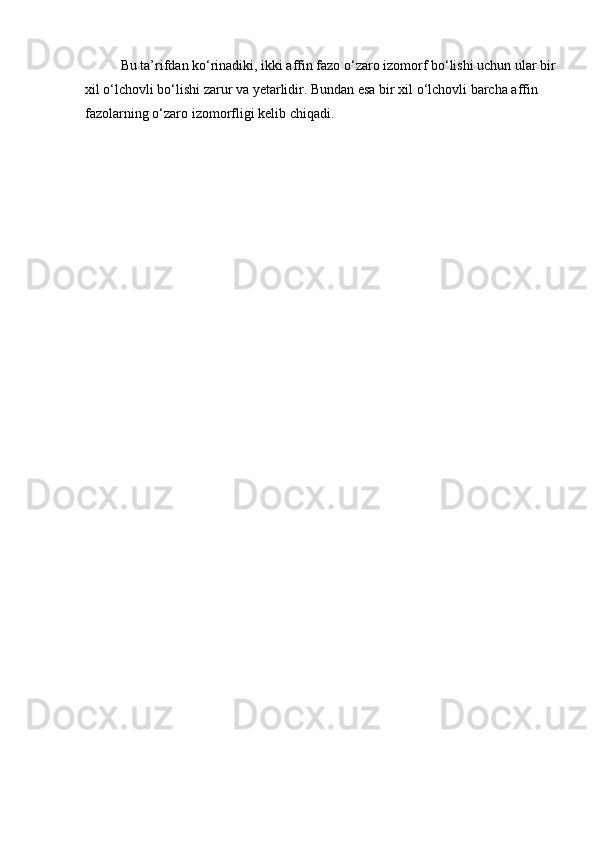
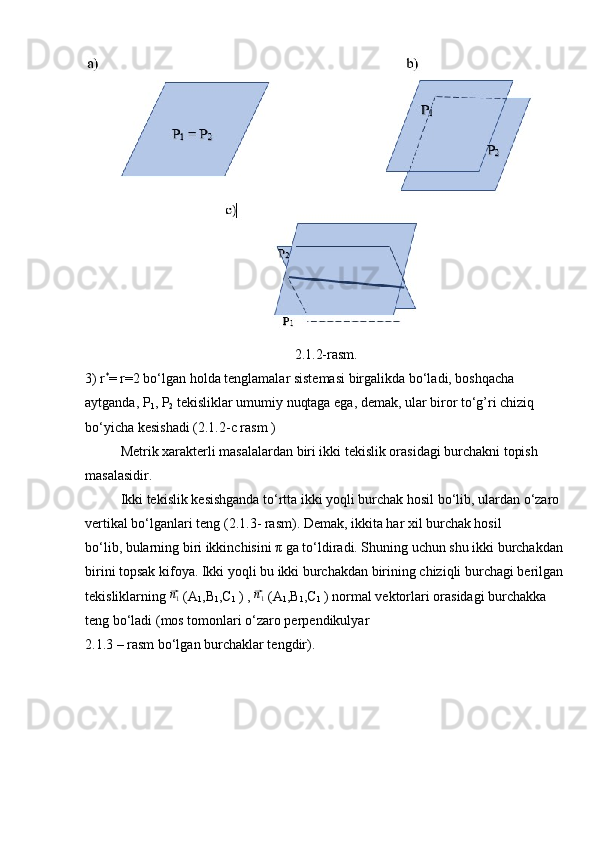
2.1.2-rasm.
3) r *
= r=2 bo‘lgan holda tenglamalar sistemasi birgalikda bo‘ladi, boshqacha
aytganda, P
1 , P
2 tekisliklar umumiy nuqtaga ega, demak, ular biror to‘g’ri chiziq
bo‘yicha kesishadi (2.1.2-c rasm )
Metrik xarakterli masalalardan biri ikki tekislik orasidagi burchakni topish
masalasidir.
Ikki tekislik kesishganda to‘rtta ikki yoqli burchak hosil bo‘lib, ulardan o‘zaro
vertikal bo‘lganlari teng (2.1.3- rasm). Demak, ikkita har xil burchak hosil
bo‘lib, bularning biri ikkinchisini π ga to‘ldiradi. Shuning uchun shu ikki burchakdan
birini topsak kifoya. Ikki yoqli bu ikki burchakdan birining chiziqli burchagi berilgan
tekisliklarning ⃗n1 (A
1 ,B
1 ,C
1 ) , ⃗n1 (A
1 ,B
1 ,C
1 ) normal vektorlari orasidagi burchakka
teng bo‘ladi (mos tomonlari o‘zaro perpendikulyar
2.1.3 – rasm bo‘lgan burchaklar tengdir).

P
1 va P
2 orasidagi burchakni φ desak, u holda quyidagi formula ikki tekislik orasida
burchakni topish formulasi hisoblanadi:
cosφ = A1A2+B1B2+C1C2
√A12+B12+C12√A22+B22+C22 (2.1.17)
Burchak kosinusi ma’lum bo‘lsa, burchakni o‘zini hisoblash osondir.
2. Uchta tekislikning o‘zaro vaziyati. Biror affin reperida tekisliklar umumiy
tenglamalar bilan berilgan bo‘lsin.
P
1 : A
1 x + B
1 y + C
1 z + D
1 = 0
P
2 : A
2 x + B
2 y + C
2 z + D
2 = 0
P
3 : A
3 x + B
3 y + C
3 z + D
3 = 0 (2.1.18)
Bu uch tekislikning vaziyatini aniqlash bu tenglamalar sistemasini yechishni
taqozo qiladi. Berilgan tenglamalarning koeffitsiyentlaridan quyidagi matritsalarni
tuzamiz:
M =
(
A1 B1 C1
A2 B2 C2
A3 B3 C3)
, M *
=
( A
1 B
1 C
1 D
1
A
2 B
2 C
2 D
2
A
3 B
3 C
3 D
3 ) .
Bu matritsalarning ranglarini mos ravishda r, r *
deb belgilaylik. Ravshanki,
1≤r≤3, 1≤r *
≤3 hamda r≤r *
.
Quyidagi hollarni ayrim-ayrim ko‘rib o‘tamiz:
1) r = 3 , r *
= 3 . Bu vaqtda yuqoridagi uchta tenglama birgalikda bo‘lib, yagona
yechimga egadir, demak, berilgan uchta tekislik bitta umumiy nuqtaga ega.(2.1.4-a
rasm).

2) r = 2 , r *
=3. M, M *
matritsalarning ranglari o‘zaro teng bo‘lmagani uchun berilgan
sistema yechimga ega emas, demak, tekisliklarning uchalasiga tegishli nuqta mavjud
emas. Lekin bu vaqtda quyidagi ikki hol bo‘lishi mumkin:
a) M matritsaning ixtiyoriy ikkita satrining elementlari proporsional emas, u holda
uchta tekislikning har ikkitasi kesishib, hosil bo‘lgan uchta to‘g’ri chiziq paralleldir
( 2.1.4-b rasm ).
b) M matritsaning tayin ikki satri elementlari proporsional bo‘lsa, shu satrlarga mos
tekisliklar parallel bo‘lib, uchinchi tekislik ularni, albatta, kesib o‘tadi ( 2.1.4-c
rasm ).
3) r = 2, r *
= 2 . Bu vaqtda M , M *
matritsalarning faqat ikki satri
elementlari proporsional bo‘lmasdan , qolgan bitta satri shu ikki satr
elementlarning chiziqli kombinatsiyasidan iborat bo‘ladi, demak, uchala tekislik
bitta to‘g’ri chiziq orqali kesishadi ( 2.1.4-d rasm ).
4) r =1 , r *
= 2 . Bu holda sistema birgalikda bo‘lmaydi, demak, P
1 , P
2 , P
3 lar
umumiy nuqtaga ega emas. Lekin r *
= 2 bo‘lgani uchun quyidagi xulosani
chiqaramiz : P
1 , P
2 , P
3 dan ikkitasi parallel bo‘lib, uchinchisi bulardan biri
bilan ustma-ust tushadi ( 2.1.4-e rasm ), yoki ularning uchalasi parallel ( 2.1.4-f
rasm ).
5) r =1 , r *
= 1 . Bu vaqtda berilgan tenglamalar sistemasi cheksiz ko‘p
yechimga ega bo‘lib, u sistema faqat bitta chiziqli erkli tenglamadan iborat
bo‘lib qoladi, demak, P
1 , P
2 , P
3 tekisliklarning uchalasi ustma-ust tushib qoladi.
Quyidagi rasmda ushbu hollarning chizmalarini ko‘rishingiz mumkin:

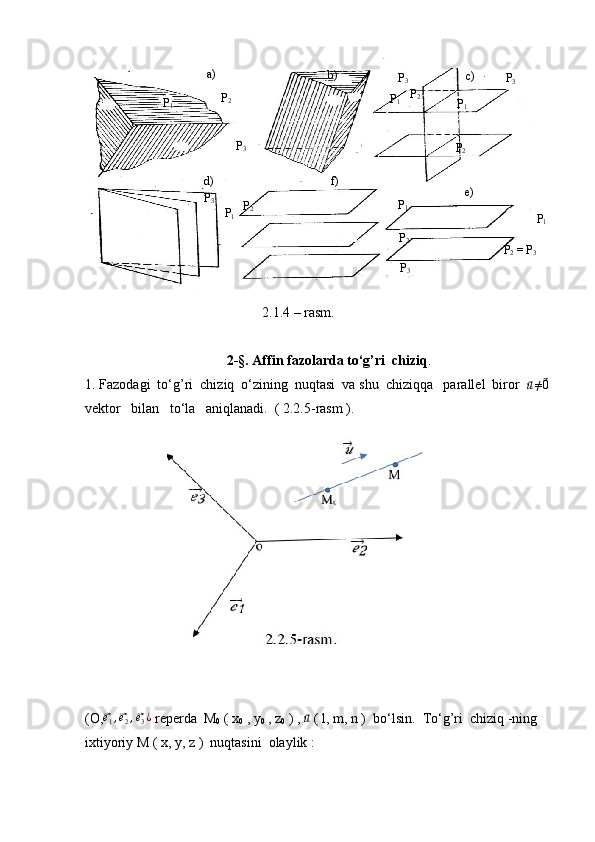
2.1.4 – rasm.
2-§. Affin fazolarda to‘g’ri chiziq .
1. Fazodagi to‘g’ri chiziq o‘zining nuqtasi va shu chiziqqa parallel biror ⃗u≠⃗0
vektor bilan to‘la aniqlanadi. ( 2.2.5-rasm ).
(O,
⃗e1,⃗e2,⃗e3¿ reperda M
0 ( x
0 , y
0 , z
0 ) , ⃗u ( l, m, n ) bo‘lsin. To‘g’ri chiziq -ning
ixtiyoriy M ( x, y, z ) nuqtasini olaylik : P
1 P
2
P
3 P
1 P
2P
3
P
1
P
2 P
3
P
1 P
2P
3
P
1
P
2
P
3 P
1
P
2 = P
3a)
b)
c)
d)
f)
e)

⃗M 0M ∥⃗u⟹ ⃗M 0M =t∙⃗u (t ∈ R) (2.2.19)
⃗
O M
0 = ⃗ r
0 , ⃗OM = ⃗r desak, hamda ⃗ M
0 M = ⃗ OM − ⃗ O M
0 ni hisobga olsak, (2.2.19)
ni quyidagicha yozish mumkin :
⃗
r = ⃗ r
0 + t ∙ ⃗ u
(2.2.20)
(2.2.20) tenglama to‘g’ri chiziqning vektorli tenglamasi deb ataladi, t ga har
xil qiymatlar berish bilan to‘g’ri chiziqqa tegishli nuqtaning radius-vektori
topiladi.
⃗M 0M
( x – x
0 , y – y
0 , z – z
0 ) va (19) dan
x – x
0 = t ∙ l x = t ∙ l + x
0
y – y
0 = t ∙ m yoki y = t ∙ m + y
0
z – z
0 = t ∙ n z = t ∙ l + z
0
(2.2.21)
Bu (2.2.21) tenglamalar sistemasi to‘g’ri chiziqning parametrik tenglamalari
deb yuritiladi. M
0 - berilgan nuqta,
⃗u esa to‘g’ri chiziqning yo‘naltiruvchi
vektori deb ataladi.
Agar l ∙ m ∙ n ≠ 0 bo‘lsa, u holda (2.2.21) ⟹ t = x − x
0
l , t = y − y
0
m , t = z − z
0
n ,
bulardan esa quyidagi natijaga erishamiz :
x − x
0
l =
y− y0
m =
z− z0
n (2.2.22)
Bu tenglamalar to‘g’ri chiziqning kanonik tenglamalari deb ataladi.
2. To‘g’ri chiziqning ikki nuqtasi uning fazodagi vaziyatini to‘la aniqlaydi:
faraz qilaylik, M
1 ( x
1 , y
1 , z
1 ) , M
2 ( x
2 , y
2 , z
2 ) nuqtalardan u to‘g’ri chiziq
o‘tsin ( M
1 ≠ M
2 ) . Oldingi banddagi M
0 nuqta o‘rniga M
1 va
⃗u=⃗M 1M 2
olinsa, (2.2.22) ga asosan .

x− x1
x2− x1 =
y− y1
y2− y1 =
z− z1
z2− z1 . (2.2.23)
(2.2.23) berilgan ikki nuqtadan o‘tuvchi to‘g’ri chiziqning tenglamalaridir.
3. Fazodagi har bir to‘g’ri chiziqni ikki tekislikning kesishish chizig’i deb
qarash mumkin. Shunga muvofiq :
P
1 : A
1 x + B
1 y + C
1 z + D
1 = 0

P
2 : A
2 x + B
2 y + C
2 z + D
2 = 0 (2.2.24)
tenglamalar sistemasi P
1 ≠ P
2 ⟹ A
1 : B
1 : C
1 ≠ A
2 : B
2 : C
2 shart bajarilganda
to‘g’ri chiziqni aniqlaydi ( 2.2.6-rasm ) .
2.2.6-rasm.
To‘g’ri chiziqning yuqorida ko‘rilgan (2.2.20) - (2.2.23) tenglamalarining
biridan qolganlariga o‘tish mumkin. Lekin u (2.2.24) ko‘rinishdagi
tenglamalari bilan berilsa, kanonik ko‘rinishga bevosita o‘tish mumkin ekanligi
ochiqdan-ochiq ravshan emas. Biz hozir shu masalaga to‘xtalamiz. Kanonik
tenglamalarni yozish uchun to‘g’ri chiziqning bitta nuqtasi va yo‘naltiruvchi
vektorini bilish kerak. (2.2.24) uch noma’lumli ikki tenglama, demak,
o‘zgaruvchilardan biriga , masalan, z ga z = z
0 qiymat berib va hosil qilingan
ikki noma’lumli ikkita tenglamani yechib, x = x
0 , y = y
0 qiymatlarni topamiz
( bunda biz | A
1 A
2
B
1 B
2 | ≠0 deb faraz qildik) . Natijada ( x
0 , y
0 , z
0 ) nuqta (2.2.24)
to‘g’ri chiziqqa tegishli bo‘ladi, u holda (2.2.24) ni quyidagicha yozib olsak
bo‘ladi :
A
1 (x – x
0 ) + B
1 (y – y
0 ) + C
1 (z – z
0 ) = 0 ,
A
2 (x – x
0 ) + B
2 (y – y
0 ) + C
2 (z – z
0 ) = 0 .
Bu sistemadan quyidagilarni topamiz :
x – x
0 =
| B
1 C
1
B
2 C
2 | t , y – y
0 = | C
1 A
1
C
2 A
2 | t , z – z
0 = | A
1 B
1
A
2 B
2 | t .
Bulardan : o
⃗e2
⃗e3
⃗
e
1 P
1
P
2u

x− x0
|
B1 C1
B2 C2|
= y− y0
|
C1 A1
C2 A2|
= z− z0
|
A1 B1
A2 B2| . (2.2.25)
Agar (2.2.24) tenglamalarni dekart reperida qarasak,
⃗n1(A1,B1,C1) vektor
P
1 tekislikning
⃗n2(A2,B2,C2) vektor P
2 tekislikning normal vektori bo‘ladi.
(2.2.25) tenglamalardagi maxrajlarda turgan ifodalar P
1 , P
2 tekisliklar normal
vektorlarining vector ko‘paytmasining mos koordinatalaridan iborat, ya’ni
⃗u[⃗n1,⃗n2]
.
Misol : M
0 ( 1, 0, -4 ) nuqtadan o‘tadigan va
⃗u ( 1, -3, 2 ) vektorga parallel
to‘g’ri chiziqning parametrik va kanonik tenglamalarini yozib, uning uchta
nuqtasini toping.
Yechish : Bu yerda x
0 = 1, y
0 = 0, z
0 = -4 va l = 1, m = -3 , n = 2; tegishli
tenglamalar quyidagi ko‘rinishni oladi :
x = 1 + t ,
y = -3t , x − 1
1 = y
− 3 = z + 4
2 .
z = -4 + 2t .
Endi shu to‘g’ri chiziqning M
0 dan tashqari yana ikki nuqtasini
topish uchun t ga ikkita qiymat beramiz :
t = 1
→ x = 2 , y = -3 , z = -2 , M
1 ( 2, -3, -2 )
t = -1
→ x = 0 , y = 3 , z = -6 , M
1 ( 0, 3, -6 ) .
Ikki to‘g’ri chiziqning o‘zaro vaziyati. Ikki to‘g’ri chiziq orasidagi
burchak. To‘g’ri chiziqlar bog’lami.
Fazoda u
1 , u
2 to‘g’ri chiziqlar biror affin reperda ushbu parametrik
tenglama-

lari bilan berilgan bo‘lsin :
x = x
1 + l
1 t , x = x
2 + l
2 t ,
u
1 : y = y
1 + m
1 t , u
2 : y = y
2 + m
2 t ,
z = z
1 + n
1 t . z = z
2 + n
2 t .
bu yerda ⃗ u
1 ( l
1 , m
1 , n
1 ) , ⃗ u
2 ( l
2 , m
2 , n
2 ) .
Fazoda ikki to‘g’ri chiziq o‘zaro parallel , kesishuvchi va ayqash
bo‘lishi mumkin. Shu holatlarni ayrim-ayrim ko‘raylik.
1. u
1 ∥
u
2
⟹ ⃗ u
1 ∥ ⃗ u
2 ⇔
l1
l2
= m1
m2
= n1
n2 . (2.2.26)
2. u
1
∩ u
2 ≠ ∅ , ya’ni u
1 , u
2 to‘g’ri chiziqlar kesishsin. Bu holda bu ikki
to‘g’ri chiziq bir tekislikka tegishli bo‘lib ,
⃗ u
1 , ⃗ u
2 , ⃗M 1M 2 vektorlar komplanar,
ya’ni (
⃗u1⃗u2⃗M 1M 2¿=0 yoki
|
l
1 m
1 n
1
l
2 m
2 n
2
x
2 − x
1 y
2 − y
1 z
2 − z
1 | = 0 (2.2.27)
(2.2.27) tenglik u
1 , u
2 to‘g’ri chiuziqlarning bir tekislikka tegishlilik shartidir.
Agar (2.2.27) shart bajarilib, (2.2.26) shart bajarilmasa , u
1 , u
2 lar bitta
nuqtada kesishadi.
3. u
1 va u
2 kesishmasa hamda parallel bo‘lmasa , ular ayqash, demak, ayqash
ikki to‘g’ri chiziq uchun
|
l1 m1 n1
l2 m2 n2
x2− x1 y2− y1 z2− z1|

≠ 0 (2.2.28)

u
1 , u
2 to‘g’ri chiziqlarning dekarft reperda qarasak, metrik xarakterli ba’zi
masalalarni hal qilish mumkin.
4. Fazodagi ikki to‘g’ri chiziq orasidagi burchak. Ikki to‘g’ri chiziq orasi-
dagi burchak deb , bu to‘g’ri chiziqlarning yo‘naltiruvchi vektorlari orasidagi
burchakka aytiladi.
Parametrik tenglamalari bilan berilgan u
1 , u
2 to‘g’ri chiziqlar uchun⃗
u
1 ( l
1 , m
1 , n
1 ) , ⃗ u
2 ( l
2 , m
2 , n
2 ) bu to‘g’ri chiziqlarning yo‘naltiruvchi vektorlaridir ,
demak ,
cos( u
1
∧ u
2 )= l
1 l
2 + m
1 m
2 + n
1 n
2
√
l
1 2
+ m
1 2
+ n
1 2 √
l
2 2
+ m
2 2
+ n
2 2 (2.2.29)
Burchakning kosinusi ma’lum bo‘lsa , bu burchakni topish osondir.
2.2.1-Ta’rif. Fazodagi tayin M
0 nuqtadan o‘tgan barcha to‘g’ri
chiziqlar to‘plami M
0 markazli to‘g’ri chiziqlar bog’lami deb ataladi. M
0 ( x
0 ,
y
0 , z
0 ) markazli bog’lam ushbu
x = x
0 + lt , y
= y
0 + mt , z = z
0 + nt
parametrik tenglamalar bilan ifodalanadi, bu yerda l, m, n bog’lamdagi har
bir to‘g’ri chiziq uchun tayin qiymatlarga ega.
Fazoda M
0 nuqtadan farqli biror M nuqta berilsa, shu M nuqtadan
bog’lamga tegishli faqat bitta to‘g’ri chiziq o‘tadi.
2.2.2-Ta’rif . Agar fazoda tayin u to‘g’ri chiziq berilgan bo‘lsa,
unga parallel barcha to‘g’ri chiziqlar to‘plami parallel to‘g’ri chiziqlar
bog’lami deb ataladi.

3-§. Affin fazoda to‘g’ri chiziq va tekislikning o‘zaro vaziyati.
Dekart reperida u to‘g’ri chiziq parametrik tenglamalari bilan, P
tekislik umumiy tenglamasi bilan berilgan bo‘lsin :
u : x = x
0 + lt , y
= y
0 + mt , z = z
0 + nt , (2.3.30) ⃗ u
(l, m, n)
P : Ax + By + Cz + D = 0 (2.3.31)
⃗n (A, B, C)
Avvalo, to‘g’ri chiziq bilan tekislikning kesishish nuqtasini topish
masalasiga to‘xtalaylik : buning uchun berilgan tenglamalarni sistema deb
qarash kerak. (2.3.30) va (2.3.31) dan
Ax
0 + By
0 + Cz
0 + D + t (Al + Bm + Cn) = 0 (2.3.32)
shartda
= - A x
0 + B y
0 + C z
0 + D
Al + Bm + Cn
(2.3.33)
bo‘ladi. ning bu qiymatini (2.3.30) ga qo‘ysak, izlangan nuqta topiladi.
Lekin
(2.3.33`)
shart bajarilsa, ya’ni
⃗u⊥⃗n bo‘lsa, u to‘g’ri chiziq ga parallel bo‘ladi.
Aksincha, ∥
⟹
⃗ u ⊥ ⃗ n ⟹ ⃗ u ∙ ⃗ n = 0
.
Demak, shart to‘g’ri chiziq bilan tekislik -ning
parallelligini bildiradi.
u ∥
P ⟹
⃗ u ⊥ ⃗ n ⟹ l
A = m
B = n
C (2.3.34)
bu (2.3.34) shart to‘g’ri chiziqning tekislikka perpendikulyarligini bildiradi.
u ∈
P bo‘lgan hol uchun to‘g’ri chiziq bilan tekislik o‘zaro vaziyatining
xususiy holidir. Bu vaqtda (2.3.33`) shart bajarilib, undan tashqari M
0
∈ P
bo‘lishi lozim, ya’ni

(2.3.35)
Demak , u ⊂
P ⟺
(2.3.33`) va (2.3.35) .
Endi to‘g’ri chiziq bilan tekislik orasidagi burchakni topish formulasini
keltiramiz.
2.3.1-Ta’rif. To‘g’ri chiziq bilan tekislik orasidagi burchak deb, to‘g’ri chiziq
bilan uning shu tekislikdagi ortogonal proyeksiyasi orasidagi burchakka aytiladi.
(quyidagi 7-rasmda keltirilgan). Biz 0 ≤ φ ≤ π
2 deb faraz qilamiz.
2.3.7-rasmdan ko‘rinadiki , φ
ning (⃗ n ∧ ⃗ u )
burchakni qabul qilish mumkin. Bu
burchak π
2 − φ
ga yoki
π
2+φ ga teng. Demak, cos ( π
2 − φ
) = sin φ yoki cos (
π
2 + φ
) = - sin φ
, shuning uchun
` sin
φ = |cos (⃗n∧⃗u)| = |Al +Bm +Cn |
√A2+B2+C2∙√l2+m2+n2 (2.3.36)
1-misol . Ushbu x = 1 + 2t , y = 3t , z = -2 + t to‘g’ri chiziq bilan 2x – y + z =
0 tekislikning kesishish nuqtasini toping.
Yechish . To‘g’ri chiziq tenglamalaridagi x, y, z ning qiymatlarini tekislik
tenglamalariga qo‘yamiz :

2 ( 1 + 2t ) – 3t + ( -2 + t ) + 1 = 0 yoki t = −1
2
U holda x = 1 + 2 (-0.5 ) = 0 , y = - 1.5 , z = - 2 – 0.5 = - 2.5 ;
izlangan nuqta ( 0, − 3
2 , − 5
2 ) .
2-misol. P (7, 9, 7) nuqtadan
x− 2
4 = y−1
3 = z
2 to‘g’ri chiziqqacha bo‘lgan
masofani toping.
Yechish. Nuqtadan to‘g’ri chiziqqacha bo‘lgan masofani topish uchun formula
berilgani yo‘q , bunday masala quyidagicha oson hal qilinad :
a) berilgan nuqtadan o‘tib, berilgan to‘g’ri chiziqqa perpendikulyar tekislik
tenglamasi tuziladi ;
b) shu tekislik bilan berilgan to‘g’ri chiziqning kesishgan nuqtasi topiladi ;
c) bu topilgan nuqta bilan berilgan nuqta orasidagi masofa topiladi.
Shu yo‘sinda masalani yechishga kirishamiz.
a) P (7, 0, 7) nuqtadan o‘tib ,
⃗n (4, 3, 2) vektorga perpendikulyar tekislikning
tenglamasini tuzamiz : 4 (x – 7) + 3 (y – 9) + 2 (z – 7) = 0 yoki
4x + 3y + 2z – 69 = 0 , (*)
b) berilgan to‘g’ri chiziq tenglamasini parametrik ko‘rinishda yozamiz :
x = 2 + 4t , y = 1 + 3t , z = 2t va bularni (*) tenglamaga qo‘yamiz :
4 (2 + 4t) + 3 (1 + 3t) + 2 ∙
2t – 69 = 0
29t – 58 = 0
t = 2
x = 2 + 4
∙ 2 = 10 ,
y = 1 + 3 ∙
2 = 7 ,
⟹ Q (10, 7, 4) nuqta to‘g’ri chiziq bilan tekislikning
√9+4+9
= 22 kesishgan nuqtasidir.
z = (2,2) = 4

XULOSA
Affin fazolarda to‘g’ri chiziq va tekisliklarga doir metrik masalalar
geometriyaning muhim va asosiy qismlaridan biridir. Bu masalalar, vektorlar,
yo‘nalish vektorlarining kombinatsiyalari, va parametrik tenglamalar orqali
geometrik obyektlarning o‘zaro munosabatlarini tushunishga yordam beradi. Affin
fazolarda to‘g’ri chiziq va tekisliklarning tenglamalarini tuzish, ular orasidagi
masofani hisoblash, hamda kesishish nuqtalarini aniqlash kabi vazifalar metrik
masalalarni yechishda asosiy o‘rin tutadi.
Kurs ishida, to‘g’ri chiziqlar va tekisliklarning matematik ifodalari, ularning
orasidagi masofa, burchaklar va kesishish masalalari mukammal tarzda tahlil qilindi.
Bu masalalarni yechishda affine operatsiyalar, skalyar va vektor ko‘paytmalaridan
foydalanishning afzalliklari ko‘rsatildi. Shuningdek, affinizatsiya va geometrik
manipulyatsiyalarning nazariy asoslari, bu tuzilmalar yordamida amaliy masalalarni
hal qilish imkoniyatlari ham yoritildi.
Affin fazolarda to‘g’ri chiziq va tekisliklar bilan ishlash, geometriyaning
boshqa sohalari bilan bog’liq bo‘lgan ko‘plab muammolarni tushunishga va
yechishga imkon yaratadi. Bu o‘z navbatida, ko‘plab ilmiy sohalarda, xususan,
kompyuter grafika, robototexnika va geodeziya kabi sohalarda qo‘llaniladi.
Yuqoridagi tahlil va hisoblashlar asosida, affin fazolarda geometrik obyektlar
orasidagi munosabatlarni o‘rganish, nafaqat nazariy, balki amaliy jihatdan ham katta
ahamiyatga ega ekanligi ko‘rinadi.

FOYDALANILGAN ADABIYOTLAR RO‘YXATI
1. Narmanov A.Y. Analitik geometriya. Toshkent . “O‘zbekiston faylasuflari milliy
jamiyati” 2020 yil , 176 bet.
2. Bayturayev A.M., Kucharov. R.R. Algebra va geometriya. Toshkent. “Innovatsiya-
Ziyo”, 2020 yil, 184 bet.
3 . Baxvalov S.V., Modenov P.S., Parxomenko A.S. Analitik geometriyadan
masalalar to‘plami. T. Universitet, 2006 yil, 442 bet.
4. Ильин В. А., Позняк Э.Г. Аналитическая геометрия. М. «Физматлит», 2004
yil , 232 стр. 4. X.Latipov, Sh.Tojiеv “Analitik gеomеtriya va chiziqli algеbra”,
T.1995 ,
5. Dadajonov N.D. , Jurayev M.SH. Geometriya. 1-qism Toshkent. 1995
6. Latipov X., Tojiyev SH., Rustamov R. Analitik geometriya va chiziqli
algebra. Toshkent . “ O ‘ qituvchi ” 1993 y
7. Клетеник Д.В., Сборник задач по аналитической геометрии. М . « Физматлит »,
2016 г , 241 стр .
8 . Boxonov.Z.S Analitik geometriyadan misol va masalalar to‘plami. Uslubiy
qo‘llanma. Nam DU 2018 yil, 106 bet.
9. Izu Vaisman . Analytical Geometry. World Scientific, USA, 2007 year,
297 p.
ELIKTRON MANBALAR.
1. htt://www.arki.ru/magaz
2. htt://www.lib.ru
3.htt://www.bilimdon.uz
4. htt://www.istedod.uz

Affin fazolarda to`gri chiziq v tekislikga doir metrik masalalar kurs ishi

Sotib olish