Ro'yxatga olish sanasi 21 Dekabr 2024
5 SotishDifferensial tenglamalarni yechishning adams usuli kurs ishi




![5o‘zgaruvchining ikki yoki undan ortiq nuqtalarda beriladi, masalan, x=a nuqtada
funksiyaning y qiymati va x=b nuqtada funksiyaning y qiymati. Chegaraviy
masalaning qo‘yilishi uchun kamida ikkita birinchi tartibli differensial tenglamalar
sistemasi yoki tartibi ikkidan kam bo‘lmagan bitta differensial tenglama berilgan
bo‘lishi lozim. Chegaraviy masalanig qo‘shimcha shartlari kesmaning chetlarida yoki
uning ichki nuqtalarida (bunday shartlar ichki chegaraviy shartlar deb ataladi)
berilishi mumkin. Chegaraviy shartlar bir necha funksiyalarning, ularning
hosilalarining yoki funksiya va uning hosilalari kombinasiyalarining yechim
izlanayotgan kesmaning bitta yoki bir nechta nuqtalaridagi qiymatlarini o‘zaro
bog‘lashi mumkin. Endi chegaraviy masalaning umumiy qo‘yilishini keltiraylik.
Faraz qilaylik, ushbu F(x, y(x), y (x), y (x),. . . , y (n) (x)) = 0 , a ≤ x ≤ b, oddiy
differensial tenglama quyidagi chegaraviy shartlar bilan berilgan bo‘lsin: φ(y(a),
y (a),...,y (n-1)(a))=0, i=1,2,...,L, ψ(y(b), y (b),...,y (n-1)(b))=0, j=L+1,...,n, bu yerda
F(x, y, y ,. . . , y (n)), φ(y, y , . . , y (n)), i=1,2,...,L, ψ(y, y ,. . . , y (n)), j=L+1,...,n –
ularning o‘zgarish sohasida berilgan va ko‘rsatilgan argumentlarning funksiyalari
bo‘lsin. L va (n-L) kesmaning o‘ng va chap chegaralarida berilgan mos shartlar soni.
Bu shartlarning umumiy soni berilgan differensial tenglamaning tartibiga teng.
Berilgan [a,b] kesmada yuqoridagi differensial tenglamani va uning mos chegaraviy
shartlarini qanoatlantiruvchi y = y(x) funksiyani topish talab etiladi. Agar bu
tenglama va uning chegaraviy shartlari izlanayotgan funksiya va uning hosilalariga
nisbatan chiziqli bo‘lsa, u holda bunday chegaraviy masala chiziqli chegraviy masala
deb ataladi. Xususiy holda, soddalik uchun, hisoblash amaliyotida ko‘p uchraydigan
ikkinchi tartibli (n=2) differensial tenglama uchun quyidagi ko‘rinishda yoziladigan
chiziqli chegaraviy masala holini qaraylik:
y +p(x)y +q(x)y = f(x), a ≤ x ≤ b, (Ω ≡[a,b]),
α
0 y(a)+ß
0 y (a) = A, α
1 y(b)+ß
1 y (b) = B,
bu yerda р(х), q(х), f(х) ∈ C
2 [a,b] – berilgan funksiyalar; α
0 ,
α
1 , ß
0 , ß
1 , A, B – berilgan sonlar,
α
j 2+ß
j 2>0, | α
j |+| ß
j |≠0, j=0,1.](https://docx.uz/documents/dd8b0eeb-b91e-4f86-9a78-8bb1ef4b77a3/page_5.png?v=1)





![11f(y, y', ....... y^n)=0
bu tеnglamada qatnashuvchi hosilalarning eng yuqori tartibi diffеrеnsial
tеnglamaning tartibi dеyiladi. Agar tеnglama izlanuvchi funksiya va uning
hosilalariga nisbatan chiziqli bo‘lsa, unga chiziqli diffеrеnsial tеnglama dеyiladi.
Aytaylik bizga birinchi tartibli y'=f(x) differentsial tenglama berilgan bo‘lib,
[x,b] kesmada x=x
0 , y=y
0 boshlang’ich shartni qanoatlantiruvchi yechimning
qiymatlarini taqribiy hisoblash masalasi qo‘yilgan bo‘lsin. Bu masala Koshi masalasi
deyiladi. Bu masalani taqribiy yechishning bir necha usullari majud bo‘lib shulardan
biri Shvetsariyalik, rus olimi, akademik Leonard Eyler usulini ko‘ramiz. Berilgan
[x
0 ,b] kesmani n ta teng bo‘lakka bo‘lib bo‘linish nuqtalari orasidagi qadam h=(b-
x
0 )/n bo'lganda nuqtalar koordinatalari x
i =x
i-1 +h. i=1,2,3, n bo‘ladi.
Boshlang’ich shartdagi x
0 va y
0 lardan foydalanib tenglama yechimining
qiymatlarini,taqriban-quyidagicha hisoblaymiz.
y
1 =y
0 +hf(x
0 ,y
0 )
y
2 =y
1 +hf(x
1 ,y
1 )
y
3 =y
2 +hf(x
2 ,y
2 )
.............................
y
n =y
n-1 +hf(x
n-1 ,y
n- 1 )
natijada izlanayotgan yechimni qanotlantiruvchi (x
0 ,y
0 ), (x
1 ,y
1 ), (x
2 ,y
2 ) ,…, (x
n ,y
n )
nuqtalarni aniqlaymiz. Bu nuqtalarni tutashtiruvchi siniq chiziq Elyer deb ataladi.
Bizga quyidagi birinchi tartibli oddiy diffеrеnsial tеnglama(Koshi masalasi) ni
y'=f(x,y)
[a,b][ oraliqdagi y=y(x
0 ) boshlang’ich shartni qanoatlantiruvchi aniq yechimi
= (x)y̅ y̅
ni topish lozim bo‘lsin.](https://docx.uz/documents/dd8b0eeb-b91e-4f86-9a78-8bb1ef4b77a3/page_11.png?v=1)
![12Koshi masalasini Eylеr usuli yordamida yechish uchun, dastlab diffеrеnsial
tеnglamaning yechimi qidiriladigan [a,b] kеsmani x
0 , x
1 , x
2 , …, x
n . tugun nuqtalar
bilan bo‘laklarga bo‘lamiz. Tugun nuqtalarning koordinatalari x
i+1 =a
i+1 h, i=( , 0̅ , 1̅
, ..., )
2̅ n̅ formula orqali aniqlanadi. Har bir tugunda y=(x
i ) yеchimning qiymatlarini
chеkli ayirmalar yordamida taqribiy ( y
i ) qiymatlar bilan almashtiriladi.
Differensial tenglamalar matematik tahlilning muhim mavzusi bo'lib, turli xil
yechim texnikasi, barqarorlik tahlili va amaliy matematikada keng qo'llaniladi.
1.2. Differensial tenglamalarni yechish usullari
Differensial tenglamalarni yechish usullari matematikaning muhim
yo‘nalishlaridan biri bo‘lib, ular ko‘plab ilmiy va texnik muammolarni hal qilishda
qo‘llaniladi. Differensial tenglamalarni yechish uchun bir nechta aniq va taxminiy
usullar mavjud. Quyida ushbu usullar haqida batafsil ma'lumot beriladi:
1. Analitik usullar
Analitik usullar differensial tenglamalarning aniq yechimini topishga asoslangan.
Bu usullar odatda faqat oddiyroq tenglamalar uchun qo‘llaniladi.
a) Ajratiladigan o‘zgaruvchilar usuli
Bu usul o‘zgaruvchilarni ajratish mumkin bo‘lgan tenglamalar uchun
qo‘llaniladi.
Tenglama:
ko‘rinishida bo‘lsa, ikki tomonning integralini olish orqali yechim topiladi:](https://docx.uz/documents/dd8b0eeb-b91e-4f86-9a78-8bb1ef4b77a3/page_12.png?v=1)














![27Quyida ikkita tenglamalarni Adams-Bashforth va Adams-Moulton usullarining
C++ da tuzilgan dasturi yordamida yechilishini ko’rib chiqamiz:
1) y’=2x-e^(-x)+1, y(0)=1
2) y’=2xsinx+(x^2)cosx, y(pi)=0
Adams-Bashforth usulida 1-tenglama uchun dastur kodi:
#include <iostream>
#include <vector>
#include <iomanip>
#include <cmath>
using namespace std;
double f(double x, double y) {
return 2 * x - exp(-x) + 1; // 1- tenglama
}
void eylerusuli(vector<double>& x, vector<double>& y, double h)
{ for (int i = 1; i < 4; ++i) {
x[i] = x[i - 1] + h;
y[i] = y[i - 1] + h * f(x[i - 1], y[i - 1]);
}
}
void adamsBashforth(double x0, double y0, double h, int N)
{ vector<double> x(N), y(N);
x[0] = x0;
y[0] = y0;](https://docx.uz/documents/dd8b0eeb-b91e-4f86-9a78-8bb1ef4b77a3/page_27.png?v=1)
![28// Boshlang'ich qiymatlarni hisoblash
eylerusuli(x, y, h);
cout << "Adams-Bashforth usuli:\n";
cout << " \n";
cout << " i\t x\t\t y\n";
cout << " \n";
for (int i = 0; i < 4; ++i) {
cout << i << "\t" << x[i] << "\t\t" << y[i] << "\n";
}
// Adams-Bashforth formulasi
for (int i = 3; i < N - 1; ++i) {
x[i + 1] = x[i] + h;
y[i + 1] = y[i] + h / 24.0 * (55 * f(x[i], y[i]) - 59 * f(x[i - 1], y[i - 1])
+ 37 * f(x[i - 2], y[i - 2]) - 9 * f(x[i - 3], y[i - 3]));
cout << i + 1 << "\t" << x[i + 1] << "\t\t" << y[i + 1] << "\n";
}
cout << " \n";
}
int main() {
double x0 = 0.0, y0 = 1.0, h = 0.1;
int N = 10;
adamsBashforth(x0, y0, h, N);
return 0;
}](https://docx.uz/documents/dd8b0eeb-b91e-4f86-9a78-8bb1ef4b77a3/page_28.png?v=1)
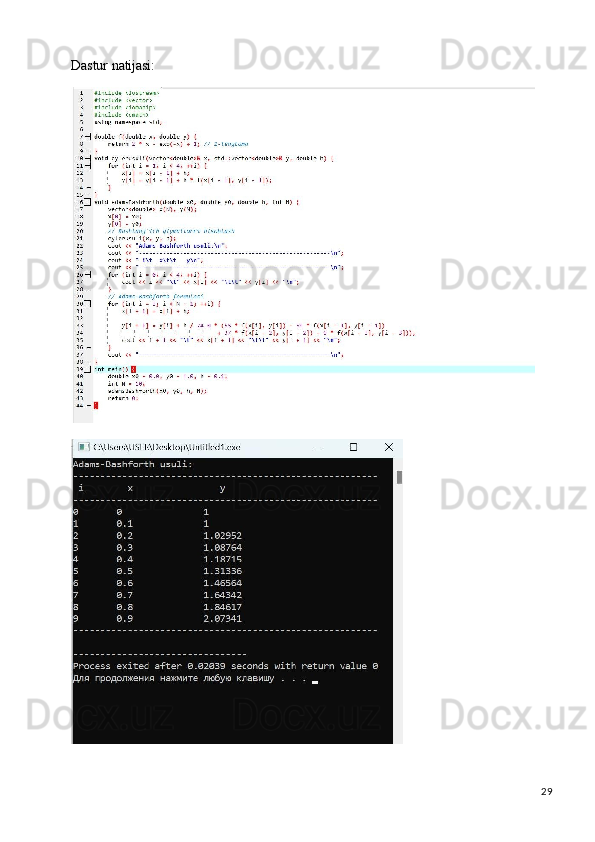
![30Endi Adams-Moulton usulida yechib ko’ramiz:
#include <iostream>
#include <vector>
#include <iomanip>
#include <cmath>
using namespace std;
double f(double x, double y) {
return 2 * x - exp(-x) + 1; // 1- tenglama
}
void eylerusuli(vector<double>& x, vector<double>& y, double h)
{ for (int i = 1; i < 4; ++i) {
x[i] = x[i - 1] + h;
y[i] = y[i - 1] + h * f(x[i - 1], y[i - 1]);
}
}
void adamsMoulton(double x0, double y0, double h, int N)
{ vector<double> x(N), y(N);
x[0] = x0;](https://docx.uz/documents/dd8b0eeb-b91e-4f86-9a78-8bb1ef4b77a3/page_30.png?v=1)
![31y[0] = y0;
eylerusuli(x, y, h);
cout << "Adams-Moulton usuli:\n";
cout << " \n";
cout << " i\t x\t\t y\n";
cout << " \n";
for (int i = 0; i < 4; ++i) {
cout << i << "\t" << x[i] << "\t\t" << y[i] << "\n";
}
for (int i = 3; i < N - 1; ++i)
{ x[i + 1] = x[i] + h;
double y_pred = y[i] + h / 24.0 * (55 * f(x[i], y[i]) - 59 * f(x[i - 1], y[i - 1])
+ 37 * f(x[i - 2], y[i - 2]) - 9 * f(x[i - 3], y[i - 3]));
y[i + 1] = y[i] + h / 24.0 * (9 * f(x[i + 1], y_pred) + 19 * f(x[i], y[i])
- 5 * f(x[i - 1], y[i - 1]) + f(x[i - 2], y[i - 2]));
cout << i + 1 << "\t" << x[i + 1] << "\t\t" << y[i + 1] << "\n";
}
cout << " \n";
}](https://docx.uz/documents/dd8b0eeb-b91e-4f86-9a78-8bb1ef4b77a3/page_31.png?v=1)
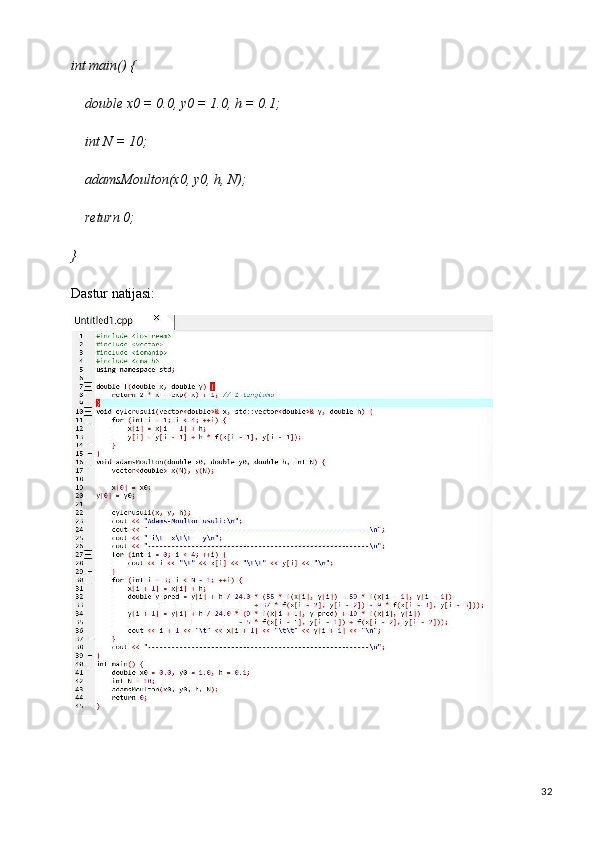

![34Adams-Bashforth usulida 2-tenglama uchun dastur kodi:
2)y’=2xsinx+(x^2)cosx, y(pi)=0
#include <iostream>
#include <vector>
#include <iomanip>
#include <cmath>
using namespace std;
double f(double x, double y) {
return 2 * x * sin(x) + x * x * cos(x); // 2- tenglama
}
void eylerusuli(vector<double>& x, vector<double>& y, double h)
{ for (int i = 1; i < 4; ++i) {
x[i] = x[i - 1] + h;
y[i] = y[i - 1] + h * f(x[i - 1], y[i - 1]);
}
}
void adamsBashforth(double x0, double y0, double h, int N)
{ vector<double> x(N), y(N);
x[0] = x0;
y[0] = y0;
eylerusuli(x, y, h);
cout << "Adams-Bashforth usuli:\n";
cout << " \n";
cout << " i\t x\t\t y\n";
cout << " \n";
for (int i = 0; i < 4; ++i) {
cout << i << "\t" << x[i] << "\t\t" << y[i] << "\n";
}
for (int i = 3; i < N - 1; ++i) {](https://docx.uz/documents/dd8b0eeb-b91e-4f86-9a78-8bb1ef4b77a3/page_34.png?v=1)
![35x[i + 1] = x[i] + h;
y[i + 1] = y[i] + h / 24.0 * (55 * f(x[i], y[i]) - 59 * f(x[i - 1], y[i - 1])
+ 37 * f(x[i - 2], y[i - 2]) - 9 * f(x[i - 3], y[i - 3]));
cout << i + 1 << "\t" << x[i + 1] << "\t\t" << y[i + 1] << "\n";
}
cout << " \n";
}
int main() {
double x0 = M_PI, y0 = 0.0, h = 0.1;
int N = 10;
adamsBashforth(x0, y0, h, N);
return 0;
}
Dastur natijasi:](https://docx.uz/documents/dd8b0eeb-b91e-4f86-9a78-8bb1ef4b77a3/page_35.png?v=1)
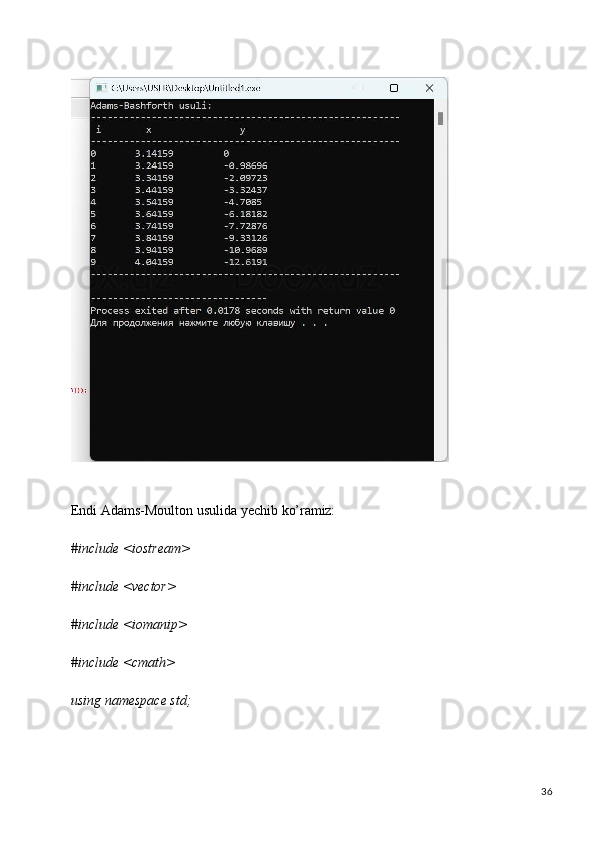
![37double f(double x, double y) {
return 2 * x * sin(x) + x * x * cos(x); // 2- tenglama
}
void eylerusuli(vector<double>& x, vector<double>& y, double h)
{ for (int i = 1; i < 4; ++i) {
x[i] = x[i - 1] + h;
y[i] = y[i - 1] + h * f(x[i - 1], y[i - 1]);
}
}
void adamsMoulton(double x0, double y0, double h, int N)
{ vector<double> x(N), y(N);
x[0] = x0;
y[0] = y0;
eylerusuli(x, y, h);
cout << "Adams-Moulton usuli:\n";
cout << " \n";
cout << " i\t x\t\t y\n";
cout << " \n";](https://docx.uz/documents/dd8b0eeb-b91e-4f86-9a78-8bb1ef4b77a3/page_37.png?v=1)
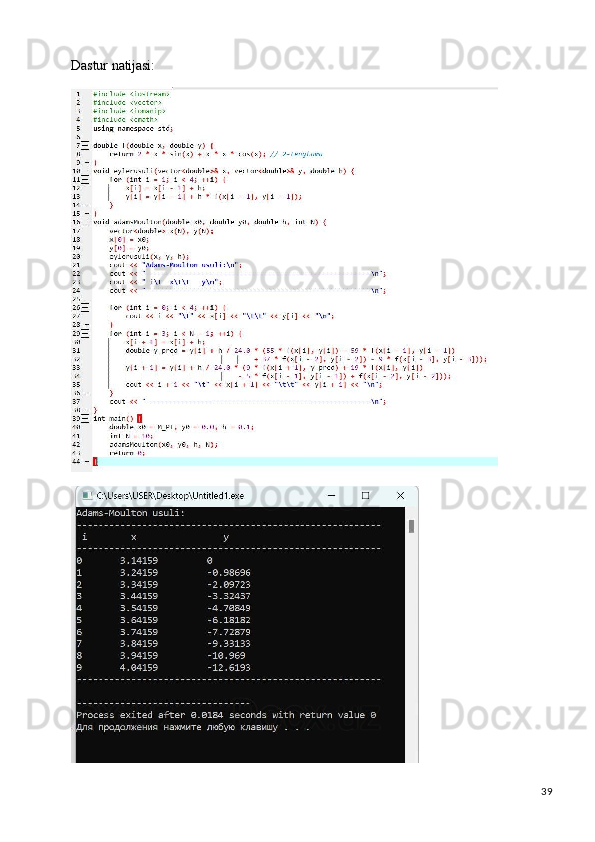
![38for (int i = 0; i < 4; ++i) {
cout << i << "\t" << x[i] << "\t\t" << y[i] << "\n";
}
for (int i = 3; i < N - 1; ++i)
{ x[i + 1] = x[i] + h;
double y_pred = y[i] + h / 24.0 * (55 * f(x[i], y[i]) - 59 * f(x[i - 1], y[i - 1])
+ 37 * f(x[i - 2], y[i - 2]) - 9 * f(x[i - 3], y[i - 3]));
y[i + 1] = y[i] + h / 24.0 * (9 * f(x[i + 1], y_pred) + 19 * f(x[i], y[i])
- 5 * f(x[i - 1], y[i - 1]) + f(x[i - 2], y[i - 2]));
cout << i + 1 << "\t" << x[i + 1] << "\t\t" << y[i + 1] << "\n";
}
cout << " \n";
}
int main() {
double x0 = M_PI, y0 = 0.0, h = 0.1;
int N = 10;
adamsMoulton(x0, y0, h, N);
return 0;
}](https://docx.uz/documents/dd8b0eeb-b91e-4f86-9a78-8bb1ef4b77a3/page_38.png?v=1)






To'liq nazariy ma'lumot va c++ tilida dastur kodi