Ro'yxatga olish sanasi 21 Aprel 2025
9 SotishNyutonning teng oraliqlar uchun ikkinchi interpolyatsion formulasining Matlab dasturidagi tadbig‘i.
![orasidagi farq nolga teng. Tugunlardan tashqarida berilgan funktsiya bilan
interpolyatsion ko'phad orasidagi xatoR(x)= f(x)− L(x)
(1.2)
bo'lsin.
y= f(x) funktsiya a≤ x≤ b oraliqda
f'(x),f''(x),...,f(n+1)(x)
(1.3)
hosilalarga ega bo'lsin. Yordamchi funktsiya kiritamiz.
u(x)= f(x)− L(x)− k∏ (x) (1.4)
Bu erda
∏ (x)=(x− x0)(x− x1)...(x− xn)
(1.5)
k
-o'zgarmas koeffitsientni keyinroq topamiz.
U(x) funktsiya ( n+1 ) ta ildizga ega
x0,x1,...,xn -nuqtalarda k koeffitsientni
shunday tanlaymizki U(x) funktsiya ( n+2 ) ta ildizga ega bo'lsin. Bu ildiz
[a,b]
oraliqda
¯x ga teng bo'lsin. Bu ildiz interpolyatsiya tugunlariga tushmasin (1-
chizma).
¯x ildizni (1.1) ga qo'ysak
U (¯x)= f(¯x)− L(¯x)− k∏ (¯x)= 0
(1.6)
bo'ladi. Bunda
k= f(¯x)− L(¯x)
∏ (¯x)
(1.7)
k ning bu qiymatlarida U(x) funktsiya ( n+2 ) ta ildizga ega bo'ladi.
[x0,x1],[x1,x2],...,[¯xi,¯x],[¯x,¯xi+1]...[¯xn−1,xn]
kesmalar oxirlarida U(x) funktsiya nolga aylanadi.](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_4.png?v=1)
![Roll teoremasiga asosan, U’(x) funktsiya ( n+1 ) ta ildizga, U’’(x) funktsiya
esa n ta ildizga ega bo'ladi. Boshqacha qilib aytganda abstsissa o'qini n ta nuqtada
kesib o'tadi.
1-chizma.
SHu mulohazani davom qildirib [a,b] oraliqda U(n+1)(x) hech bo'lmasa bitta
ildizga ega bo'ladi. Bu ildizni
ξ bilan belgilaymiz, ya'ni U(n+1)(ξ) =0 bo'ladi.
(1.6) formuladan
Lξ
(n+1)(x)=0
va
∏
(n+1)(x)=(n+1)!
∏
(n+1)(x)= f(n+1)(x)− k(n+1)!
bo'ladi.
x= ξ da
0= f(n+1)(ξ)− k(n+1)!
(1.8)
ega bo'lamiz. Bundan
k= f(n+1)(ξ)
(n+1)!
(1.8)
(2) bilan (3) ni solishtirsak,](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_5.png?v=1)
![f(¯x)− L(¯x)
∏ (¯x)
= f(n+1)(ξ)
(n+1)! (1.9)
Bundan
f(¯x)− L(¯x)= f(n+1)(ξ)
(n+1)! ∏ (¯x)
(1.10)
bo'ladi.
¯x nuqta ixtiyoriy bo'lgani uchun (4) ni quyidagicha yozish mumkin.
R(x)= f(x)− L(x)= f(n+1)(ξ)
(n+1)! ∏ (x)
(1.11)
bu erda
ξ nuqta x ga bog'liq va [a,b] oraliqda yotadi.
(1.5) formula [a,b] oraliqdagi hamma nuqtalar uchun yaroqli shu jumladan
interpolyatsiya tugunlarida ham.
M = maxa≤x≤b|f(n+1)(x)|
belgilab olamiz. U vaqtda interpolyatsion formulaning absolyu xatoligi
|R(x)|=|f(x)− L(x)|≤ M
(n+1)!∏ (x)
(1.12)
bo'ladi. Bu erda
∏ (x)=(x− x0)(x− x1)...(x− xn)
Misol.
y= √x funktsiya uchun x0= 100 , x1= 121 , x2= 144
interpolyatsiya tugunlarida Logranj interpolyatsiya formulasi yordamida
√115 ni
qanday aniqlikda hisoblash mumkin.
Yechish:
y'= 1
2 x
−1
2, y''= − 1
4 x
−3
2, y'''= 3
8 x
−5
2
larni topib olamiz.](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_6.png?v=1)
![1- Masala
Interpolatsiya polinomini topish (yangi nuqtada qiymatni hisoblash)
Ma'lumotlar:
x = [0, 1, 2, 3]
y = [1, 2, 0, 5]
X = 1.5 Interpolatsiya qilish nuqtasi
Masalaning kodi:
% Ma'lumotlar
x = [0, 1, 2, 3];
y = [1, 2, 0, 5];
X = 1.5; % Interpolatsiya nuqtasi
% Ikkinchi differensial formulani hisoblash
n = length(x);
a = y; % a_0, a_1, ...
% Birinchi differensialni hisoblash
for i = 2:n
for j = n:-1:i
a(j) = (a(j) - a(j-1)) / (x(j) - x(j-i+1));
end
end
% Interpolatsiya polinomi](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_13.png?v=1)
![syms X_sym ;
P = a(n);
for i = n-1:-1:1
P = a(i) + (X_sym - x(i)) * P;
end
% Yangi nuqtada qiymatni hisoblash
result = double(subs(P, X_sym, X));
disp([ 'Interpolatsiya qiymati X = ' , num2str(X), ' uchun: ' , num2str(result)]);
Natija:
Interpolatsiya qiymati X = 1.5 uchun: 0.75
2- Masala
Masala: Interpolatsiya polinomini topish
Ma'lumotlar:
x = [1, 2, 3]
y = [1, 4, 9]
MATLAB kodi:
% Ma'lumotlar
x = [1, 2, 3];
y = [1, 4, 9];
% Ikkinchi differensial formulani hisoblash
n = length(x);](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_14.png?v=1)
![a = y; % a_0, a_1, ...
% Birinchi differensialni hisoblash
for i = 2:n
for j = n:-1:i
a(j) = (a(j) - a(j-1)) / (x(j) - x(j-i+1));
end
end
% Interpolatsiya polinomi
syms X ;
P = a(n);
for i = n-1:-1:1
P = a(i) + (X - x(i)) * P;
end
disp( 'Interpolatsiya polinomi:' );
disp(P);
Natija:
Interpolatsiya polinomi: (X - 1)*(X + 1) + 1
3 -masala
$\ln(x)$ funksiyasining Nyuton interpolatsiyasi
Matlab kodi:
% Nuqtalar
x = [1 2 3];](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_15.png?v=1)
![4-masala
$\cos(x)$ funksiyasining Nyuton interpolatsiyasi
Matlabda kodi:
% Nyuton interpolatsiyasi uchun differensial operatorini hisoblash
n = length(x);
D = zeros(n,n);
D(:,1) = y';
for j = 2:n
for i = 1:n-j+1
D(i,j) = (D(i+1,j-1) - D(i,j-1)) / (x(i+j-1) - x(i));
end
end
% Interpolatsiya polinomini hisoblash
P = @(xx) D(1,1) + (xx - x(1)) * D(1,2) + (xx - x(1))*(xx - x(2)) * D(1,3);
% Grafika chizish
xx = linspace(0, 2*pi/3, 100);
yy = P(xx);
plot(xx, yy, 'r' , x, y, 'bo' );
title( 'Nyuton Interpolatsiyasi: cos(x)' );
legend( 'Interpolatsiya' , 'Nuqtalar' );
Natijasi: Grafikda cos(x) funksiyasi interpolyatsiya polinomi bilan
yaqinlashtiriladi.
x=[0, π /3,2 π /3] nuqtalarida polinom funksiyaning asl qiymatlari bilan bir xil
bo‘ladi:
P(0)=cos (0) =1,
P ( π /3)=cos( π /3)=0.5,
P(2 π /3)=cos(2 π /3)= -0.5](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_17.png?v=1)
![5-masala
% Nuqtalar
x = [0 pi/3 2*pi/3];
y = cos(x);
% Newton's Second Interpolation Formula
% Define x and y values
x_vals = [1, 2, 3, 4];
y_vals = [1, 8, 27, 64]; % y = x^3
% Interpolation point
x = 2.5;
% Number of points
n = length(x_vals);
% Step size (h)
h = x_vals(2) - x_vals(1);
% Construct the difference table
diff_table = zeros(n, n);
diff_table(:, 1) = y_vals;
for j = 2:n
for i = 1:n-j+1
diff_table(i, j) = diff_table(i+1, j-1) - diff_table(i, j-1);
end
end
% Calculate u
u = (x - x_vals(1)) / h;
% Interpolation using Newton's formula
result = y_vals(1); % Start with the first term](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_18.png?v=1)
![term = 1;
for k = 1:n-1
term = term * (u - (k-1)) / k;
result = result + term * diff_table(1, k+1);
end
% Display the result
disp([ 'Interpolated value at x = ' , num2str(x), ' is: ' , num2str(result)]);
Natija: Interpolated value at x = 2.5 is: 15.625
6-masala
% Calculate u
u = (x - x_vals(1)) / h;
% Interpolation using Newton's formula
result = y_vals(1); % Start with the first term
term = 1;
for k = 1:n-1
term = term * (u - (k-1)) / k;
result = result + term * diff_table(1, k+1);
end
% Display the result% Newton's Second Interpolation Formula Example 2
% Define x and y values
x_vals = [1, 2, 3, 4];
y_vals = [1, 4, 9, 16]; % y = x^2
% Interpolation point
x = 2.5;
% Number of points](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_19.png?v=1)
![n = length(x_vals);
% Step size (h)
h = x_vals(2) - x_vals(1);
% Construct the difference table
diff_table = zeros(n, n);
diff_table(:, 1) = y_vals;
for j = 2:n
for i = 1:n-j+1
diff_table(i, j) = diff_table(i+1, j-1) - diff_table(i, j-1);
end
end
disp([ 'Interpolated value at x = ' , num2str(x), ' is: ' , num2str(result)]);
Natijasi:
Interpolated value at x = 2.5 is: 6.25
7-Masala
% Define x and y values
x_vals = [0, 1, 2, 3];
y_vals = exp(x_vals); % y = e^x
% Interpolation point
x = 1.5;
% Number of points
n = length(x_vals);
% Step size (h)
h = x_vals(2) - x_vals(1);
% Construct the difference table
diff_table = zeros(n, n);
diff_table(:, 1) = y_vals;
for j = 2:n
for i = 1:n-j+1](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_20.png?v=1)
![diff_table(i, j) = diff_table(i+1, j-1) - diff_table(i, j-1);
end
end
% Calculate u
u = (x - x_vals(1)) / h;
% Interpolation using Newton's formula
result = y_vals(1); % Start with the first term
term = 1;
for k = 1:n-1
term = term * (u - (k-1)) / k;
result = result + term * diff_table(1, k+1);
end
% Display the result
disp([ 'Interpolated value at x = ' , num2str(x), ' is: ' , num2str(result)]);
Natijasi:
Interpolated value at x = 1.5 is: 4.3675
8-Masala
y = sin ( x ) funksiyasi uchun qizil chiziq haqiqiy qiymatlar, ko'k nuqtali chiziq esa
interpolyatsiyalangan qiymatlarni ifodalaydi.
% Newton's Second Interpolation Formula with Graph (Sin function)
% Define x and y values
x_vals = [0, pi/6, pi/3, pi/2];
y_vals = sin(x_vals);
% Interpolation points
x_interpolate = linspace(0, pi/2, 100);
y_interpolated = zeros(size(x_interpolate));
% Step size (h)
n = length(x_vals);](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_21.png?v=1)
![xlabel( 'x' );
ylabel( 'y' );
grid on ;
Natija:
10 -masala
y = x^3 funksiyasi uchun haqiqiy (qizil) va interpolyatsiyalangan (ko'k) grafiklar
o'xshash bo'ladi.
% Newton's Second Interpolation Formula with Graph (Cubic function)
% Define x and y values
x_vals = [1, 2, 3, 4];
y_vals = x_vals.^3;
% Interpolation points
x_interpolate = linspace(1, 4, 100);
y_interpolated = zeros(size(x_interpolate));
% Step size (h)](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_23.png?v=1)
![scatter(x_vals, y_vals, 'ko' , 'filled' );
legend( 'Exact x^3' , 'Interpolated' , 'Data Points' );
title( 'Newton Interpolation for x^3' );
xlabel( 'x' );
ylabel( 'y' );
grid on ;
Natija:
11-Masala
% % Newton's Second Interpolation Formula with Graph (Logarithmic function)
Define x and y values
x_vals = [1, 2, 3, 4];
y_vals = log(x_vals); % y = ln(x)
% Interpolation points
x_interpolate = linspace(1, 4, 100);
y_interpolated = zeros(size(x_interpolate));](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_25.png?v=1)
![plot(x_interpolate, y_interpolated, 'b--' , 'LineWidth' , 1.5);
scatter(x_vals, y_vals, 'ko' , 'filled' );
legend( 'Exact ln(x)' , 'Interpolated' , 'Data Points' );
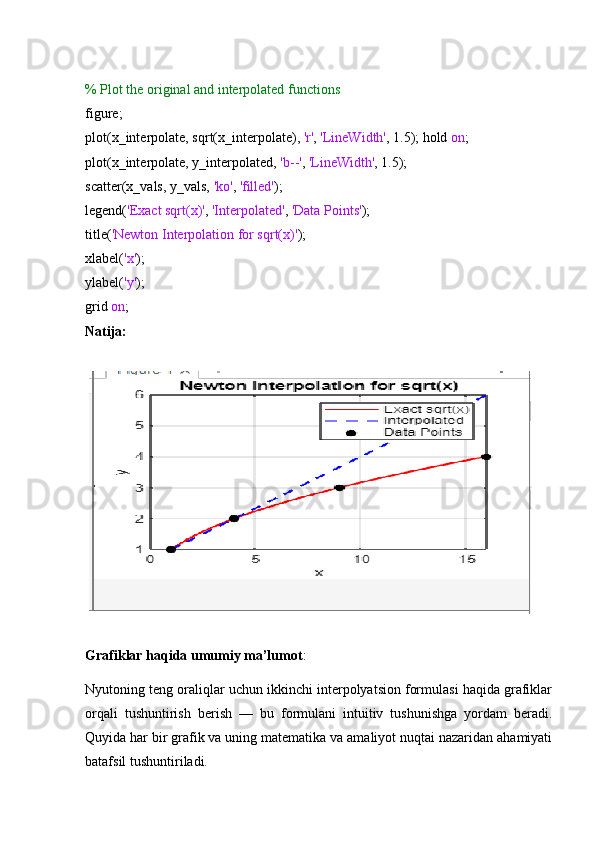
title( 'Newton Interpolation for ln(x)' );
xlabel( 'x' );
ylabel( 'y' );
grid on ;
Natija:
12-masala
% Newton's Second Interpolation Formula with Graph (Square Root function)
% Define x and y values
x_vals = [1, 4, 9, 16];
y_vals = sqrt(x_vals); % y = sqrt(x)](https://docx.uz/documents/38e98e70-7fdb-4a12-9a70-e16394f92dad/page_27.png?v=1)
Nyutonning teng oraliqlar uchun ikkinchi interpolyatsion formulasining Matlab dasturidagi tadbig‘i.
-
O'xshash dokumentlar
- Ikkinchi tartibli sirtning asimptotik konusi va diametral tekisligi
- Fazoda tekislik va to`g`ri chiziqning o`zaro joylashuvi
- Bir pallali giperboloid va giperbolik paraboloidning to’g’ri chiziqli yasovchilari
- Tekislikda koordinatalar metodi
- Ikkinchi tartibli chiziqni tenglamasiga ko’ra yasash