Ro'yxatga olish sanasi 14 Fevral 2025
154 SotishTekislik va to‘g‘ri chiziqning o‘zaro vaziyati









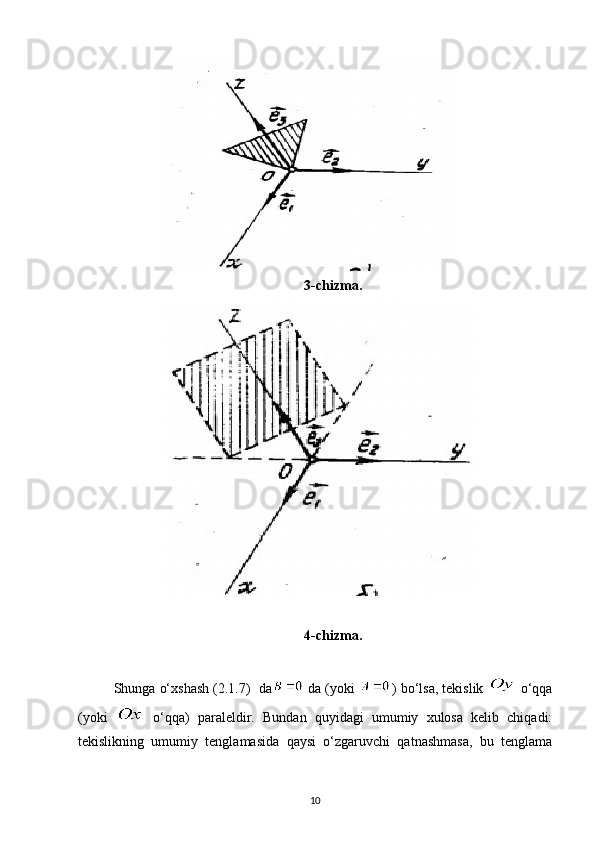

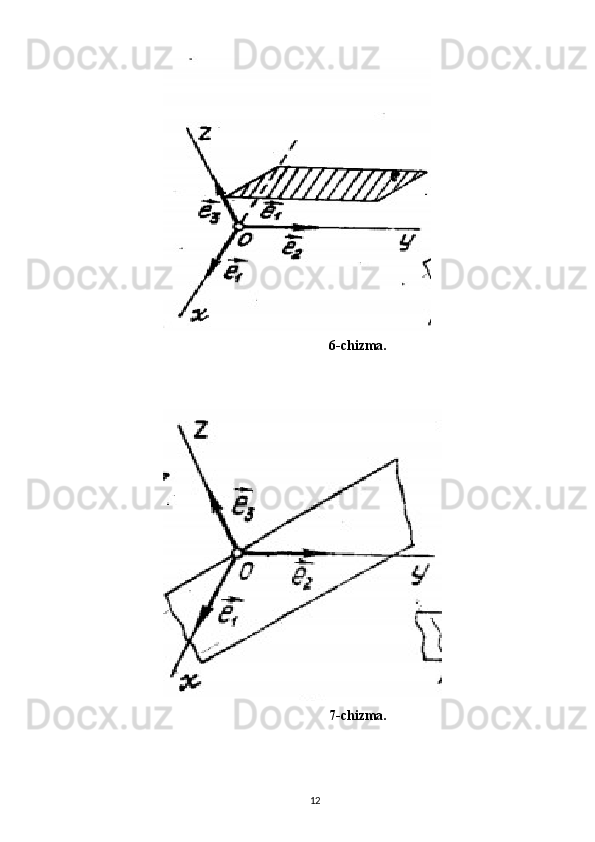
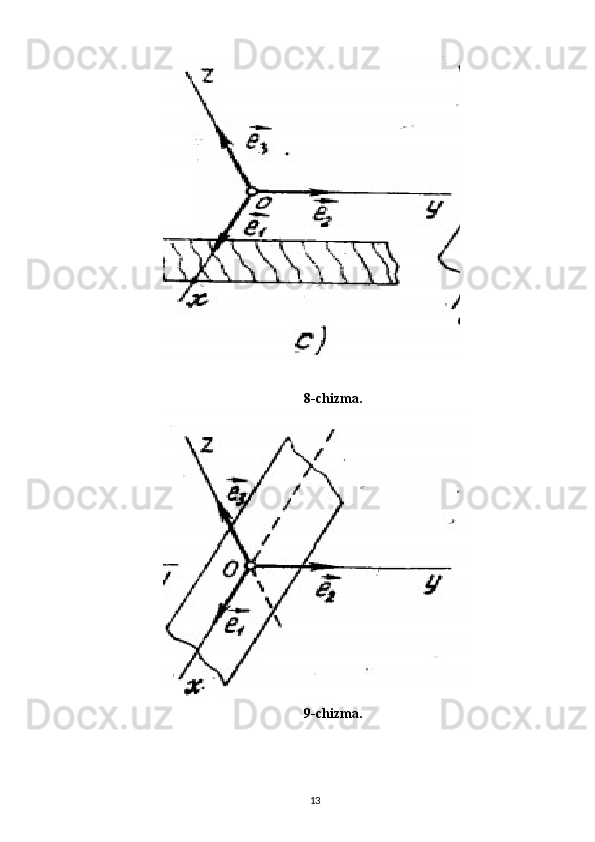




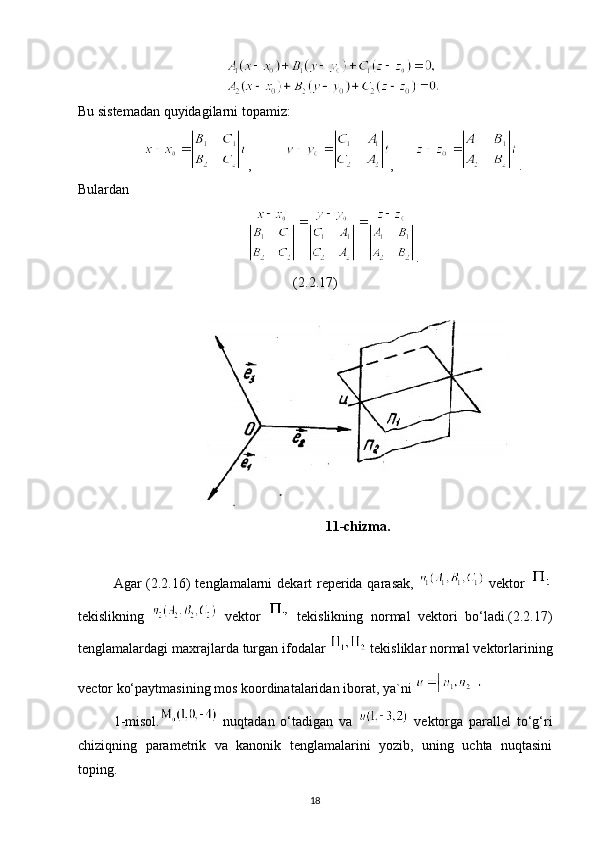




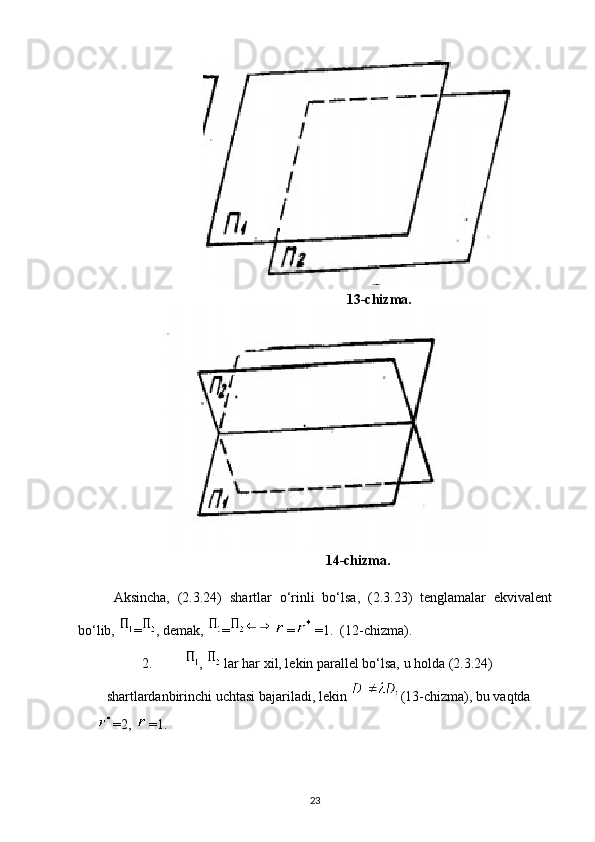



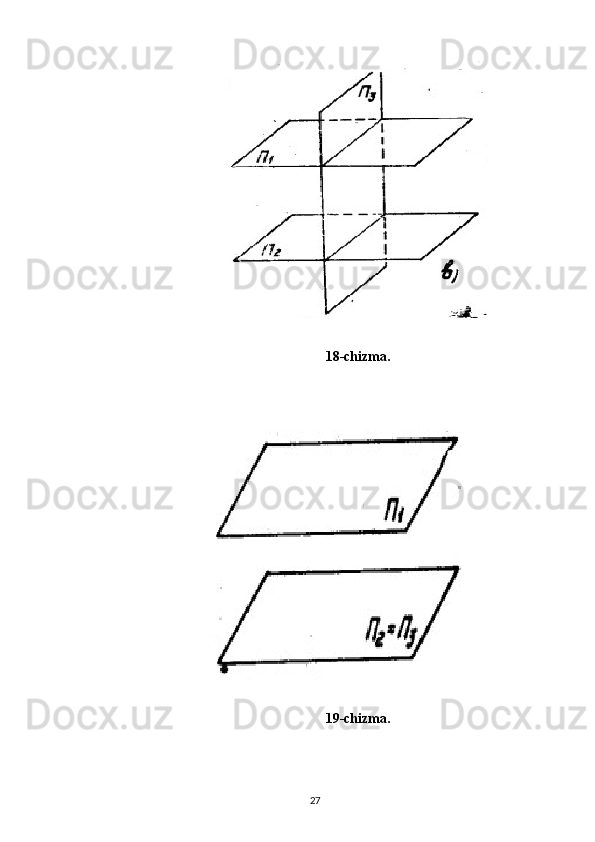
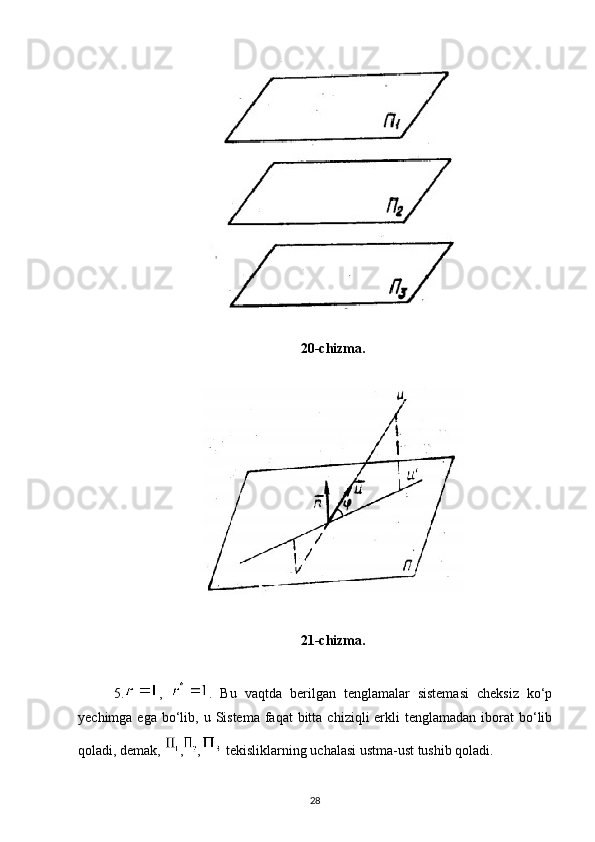







Tekislik va to‘g‘ri chiziqning o‘zaro vaziyati