Aniq integrallarning geometriyaga tatbiqlari - Алгебра - Курсовые работы

Информация о документе

Цена	30000UZS
Размер	1.2MB
Покупки	0
Дата загрузки	11 Июнь 2025
Расширение	docx
Раздел	Курсовые работы
Предмет	Алгебра

Продавец

G'ayrat Ziyayev

Дата регистрации 14 Февраль 2025

167 Продаж

Aniq integrallarning geometriyaga tatbiqlari

Купить

O‘ZBEKISTON RESPUBLIKASI
OLIY TA’LIM FAN VA INNOVATSIYALAR VAZIRLIGI
Farg‘ona davlat universiteti
Fizika-Matematika fakulteti
“Matematik analiz va differensial tenglamalar ” kafedrasi
Matematik analiz fanidan
KURS ISHI
Mavzu: “ Aniq integrallarning geometriyaga tatbiqlari ”
Bajardi: -guruhi talabasi
Ilmiy rahbari: “Matematik analiz va differensial tenglamalar
kafedrasi mudiri.
FARG ‘ ONA–202 5

REJA:
1

KIRISH.
ASOSIY QISM
1 -§ .Aniq integral haqida tushuncha ……………………………………..6
2 -§ . Aniq integral yordamida yuzalarni hisoblash……………………....11
3 -§ . Aniq integral yordamida egri chiziq yoyi uzunligini hisoblash…...18
4 -§ . Aylanish jismlarining hajmlarini hisoblash………………………...22
5 -§ . Sirtlarning yuzalarini hisoblash……………………………………..25
XULOSA …………………………………………………………………32
FOYDALANILGAN ADABIYOTLAR .................................................33
2

“Agar mendan sizni nima qiynaydi?” deb
so‘rasangiz, farzandlarimizning ta’lim
tarbiyasi deb javob beraman!!!
Shavkat Mirziyoyev
KIRISH.
Ilg‘or millat va rivojlangan davlat bo‘lishning zarur shartlaridan biri aqliy va
jismoniy, ma’daniy va ma’naviy, axloqiy, g‘oyaviy – siyosiy va huquqiy jihatdan
har tomonlama yetuk, barkamol insonlarga ega bo‘lishdir.
Ma’naviy–ma’rifiy jihatdan inson, inson irodasi mustahkam, e’tiqodi
yuksak, vijdon amri bilan yashaydigan shaxs, barkamol avlod har qanday davlat,
xalq va millatning eng katta boyligi, qudrati salohiyati manbaidir. Mamlakatimiz
prezidenti tomonidan ta’kidlab kelinayotganidek, “Har qaysi davlat, har qaysi
millat nafaqat yerosti va yerusti boyliklari bilan, harbiy qudrati va ishlab chiqarish
salohiyati bilan, balki birinchi navbatda o‘zining yuksak madaniyati va
ma’naviyati bilan kuchlidir”.
Odamlari, fuqarolari bilimli–zakovatli, uddaburon, g‘oyaviy siyosiy jhatdan
ziyrak va hushyor, tadbirkor, har tomonlama yetuk bo‘lgan jamiyat har qanday
islohotlarga qodir bo‘ladi va har qanday muammo va qiyinchiliklarni yenga oladi.
Oliy rahbarimiz bu haqida shunday dedi: “Lo‘nda qilib aytganda, bugungi kunda
oldimizda qo‘ygan buyuk maqsadlarimizga, ezgu niyatlartimizga erishishimizda
jamiyatimizning yangilanishi, hayotimizning taraqqiyoti va istiqboli amalga
oshirayotgan islohotlarimiz, rejalarimizning samarasi taqdiri bularning barchasi
avvalambor zamon talablariga javob beradigan yuqori malakali, ongli mutaxassis
kadrlar tayyorlash muammosi bilan chambarchas bog‘liqligini barchamiz anglab
yetmoqdamiz.
Shu bilan birga barchamiz yana bir haqiqatni anglab yetmoqdamiz.
Faqatgina chinakam ma’rifatli odam inson qadrini, millat qadriyatlarini, bir so‘z
bilan aytganda, o‘zligini aniqlash, erkin va ozod jamiyatda yashash, mustaqil
davlatimizning jahon hamjamiyatida o‘ziga munosib, fidoiylik bilan kurashishi
mumkin”. Mustaqil va erkin fikrlayotgan, ongli yashaydigan, o‘z haq–huquqlarini
3

yaxshi taniydigan, o‘z kuchi va aqliga ishonadigan, ma’naviy–axloqiy yetuk
barkamol bo‘lgan avlodni, mustaqil fikrlashga qodir, jasoratli, fidoiy va
tashabbuskor kishilarni tarbiyalab yetkazadigan xalq va millat kelajakka ochiq
ko‘z, katta ishonch, umid va ixlos bilan qaray oladi. Fuqarolarni ana shunday
noyob xislat va fazilat sohiblari qilib shakllantirilgan davlatning istiqboli porloq
bo‘ladi.
Kurs ishining dolzarbligi: Yoshlarga ta’lim va tarbiya berishning murakkab
vazifalarini hal etish o‘qituvchining g‘oyaviy e ’ tiqodi, kasb-mahoratiga, san’ati,
iste’dodi va madaniyatiga hal qiluvchi darajada bog‘liqdir. Ta’lim- t arbiya
jarayonini to‘g‘ri tashkil etish uchun barcha mavjud imkoniyatlarini safarbar etish
o‘qituvchilarning birinchi navbatdagi vazifalaridan biridi r. Matematika fani o‘sib
kelayotgan yosh avlodni kamol toptirishda o‘quv fani sifatida keng imkoniyatlarga
ega. U o‘quvchi tafakkurini rivojlantirib, ularning aqlini peshlaydi, uni tartibga
soladi, o‘quvchilarda maqsadga yo‘naltirganlik, mantiqiy fikrlash, topqirlik
xislatlarini shakllantirib boradi. Shu bilan bir qatorda mulohazalarning to‘g‘ri,
go‘zal tuzilganligi, o‘quvchilarni didli, go‘zallikka ehtiyojli qilib tarbiyalab boradi.
Insoniyat kamoloti hayotning rivoji texnika va texnologiyalarning
takomillashib borish asosida fanlar o‘qitilishiga bo‘lgan talablarini hisobga olgan
holda maktab matematika kursini ularning zamonaviy rivoji bilan uyg‘unlashtirish
maktabda o‘quvchilarga matematikani o‘qitishdan ko‘zda tutilgan asosiy
maqsadlardan biridir.Matematika fani o‘quvchilarni iroda, diqqatni to‘plab olishni;
qobiliyat va faollikni, tasavvurining rivojlangan bo‘lishini talab eta borib, mustaqil,
ma’suliyatli, mehnatsevar, intizomli va mantiqiy fikrlash hamda o‘zining qarash va
e’tiqodlarini dalillar asosida himoya qila olish ko‘nikmalarini rivojlantirishni talab
qiladi. Hozirgi zamon darsiga qo‘yiladigan eng muhim talablardan biri har bir
darsda tanlanadigan mavzuning ilmiy asoslangan bo‘lishidir, ya’ni darsdan
ko‘zlangan maqsad hamda o‘quvchilar imkoniyatini hisobga olgan holda mavzu
xajmini belgilash uning murakkabligini aniqlash, avvalgi o‘rganilgan mavzu bilan
bog‘lash, o‘quvchilarga beriladigan topshiriq va mustaqil ishlarning ketma-
ketligini aniqlash, darsda kerak bo‘ladigan jihozlarni belgilash va qo‘shimcha
4

ko‘rgazmali qurollar bilan boyitish, qo‘shimcha axborot texnologiyalardan
foydalangan holda muammoli vaziyatni yaratishdir. Dars davomida o‘qituvchi
o‘quvchilarning jismoniy holatini, ijodkorligini, tez fikrlashlarini hisobga olishi
kerak.
Kurs ishining maqsadi va vazifalari: Matematik analiz kursi davomida
Aniq integral haqida olgan bilim ko’nikmalarni mustahkamlash. Aniq
integrallarning geometriyaga tatbiqlari haqida chuqurroq bilimlarga ega bo’lish.
1. Mavzuga doir ma’lumotlarni yig’ish va rejani shakllantirish.
2. Matematik analiz fanini chuqurroq o’rganish.
3. Elementar matematikani yaxshiroq o’rganish.
4. Aniq integrallarning geometriyaga tatbiqlarining yaxshiroq
o’rganish.
5. Kurs ishini jihozlab uni himoyaga tayyor qilish.
5

1 -§ . Aniq integral haqida tushuncha
funksiya kesmada aniqlangan bo‘lsin.
1-ta’rif. Ushbu
tengsizlikning qanoatlantiruvchi , chekli nuqtalar to’plamiga
kesmaning bo’linishi deb ataladi. nuqtani olib, quyidagi yig’indini
tuzamiz:
(1)
(1) yig’indining funksiyaning kesmaning berilgan bo’linishi va
tanlangan nuqtalariga mos integral yig’indisi yoki Riman integral yig’indisi deb
ataladi.
(1) integral yig’indining bo’linishdiametri nolga intilgandagi limitini qaraylik:
(2)
Agar kesmaning har qanday bo’linishi olinganda ham (2) limit
nuqtalarning tanlab olinishiga bog’liq bo’lmagan holda har doim bir xil songa
intilsa, u holda funksiya kesmada Riman ma’nosida integrallanuvchi
funksiya deyiladi, limitning qiymati esa funksiyaning kesma bo’yicha
aniq integrali deyiladi va quyidagicha belgilanadi:
.
a soni – integralning quyi chegarasi, b soni esa integralning yuqori chegarasi
deyiladi , - integral osti funksiya , - integral ostidagi ifoda deyiladi.
integralning hisoblashga funksiyaning kesmada integrallash
deyiladi.
6

Agar da bo’lsa, u holda aniq integralning
geometrik ma’nosi , , va chiziqlar bilan
chegaralangan figura – egri chiziqli figura yuzini ifodalaydi.
2.Aniq integralning xossalari.
Aniq integral quyidagi xossalarga ega:
1.
2.
3.
4.
5. bu yerda c-ixtiyoriy o’zgarmas son.
6. Agar bo’lib, uchun bo’lsa, u holda
.
7. Agar bo’lib, uchun bo’lsa, u holda
8. Agar funksiya da chegaralangan bo‘lsa, ya’ni shunday m, M sonlar
topilib, uchun tengsizlik o‘rinli bo‘lsa, u holda
funksiyaning oraliq bo‘yicha aniq integrali uchun quyidagi baho o‘rinli:
.
7

9. Agar funksiya kesmada uzluksiz bo‘lsa, u holda shunday
nuqta topiladiki, quyidagi tenglik o‘rinli bo‘ladi (o‘rta qiymat
haqidagi teorema).
10. Agar funksiya uzluksiz va bo‘lsa, u holda
tenglik o‘rinli, ya’ni uzluksiz funksiyadan yuqori chegarasi o‘zgaruvchi bo‘lgan
aniq integralning hosilasi mavjud va u integral ostidagi funksiyaning dagi
qiymatiga teng.
3. Aniq integralni hisoblash. Agar funksiya da uzluksiz va
uning biror boshlang‘ich funksiyasi bo‘lsa, u holda quyidagi Nyuton-Leybnits
formulasi o‘rinli:
. (3)
Agar funksiya kesmada uzluksiz, funksiya esa
differensiallanuvchi bo‘lib, shu bilan birga bo‘lsa, u holda
ushbu tenglik o‘rinli:
. (4)
(4) formula aniq integralda o‘zgaruvchilarni almashtirish formulasi deb ataladi.
Ko‘pincha almashtirish o‘rniga teskari almashtirishdan
foydalaniladi. Bu holda integrallashning yangi chegaralari va bevosita
va tengliklardan topiladi.
Agar funksiyalar va ularning hosilalari
kesmada uzluksiz bo‘lsa, u holda ushbu
. (5)
8

tenglik o‘rinli. (5) formula aniq integral uchun bo‘laklab integrallash formulasi deb
ataladi.
Amaliy masalalarni yechishda quyidagi faktlardan foydalanish qulaylik yaratadi:
. Agar funksiya toq funksiya bo‘lsa, u holda ushbu tenglik o‘rinli:
.
. Agar juft funksiya bo‘lsa, u holda quyidagi
tenglik o‘rinli.
. Agar funksiya davriy funksiya bo‘lib, uning davri T ga teng bo‘lsa, u
holda ixtiyoriy uchun ushbu tenglik o‘rinli:
.
1-misol. Ushbu
integral integral yig‘indining limiti sifatida hisoblansin(aniq integral ta’rifi
yordamida).
Yechish. Bu misol uchun kesmani n ta teng
bo‘laklarga bo‘lamiz va sifatida har bir bo‘linish oralig‘ining o‘ng
cheti ya’ni ni tanlab olaylik. U holda
…….
bo‘lib, lar uchun quyidagilarga ega bo‘lamiz:
9

……….
Oxirgi tengliklardan ko‘rsatish qiyin emaski,
Topilganlarni (1) integral yig‘indiga qo‘yib, da ekanligini e’tiborga
olib, quyidagiga ega bo‘lamiz:
.
Ma’lumki, ushbu formula o‘rinli:
.
U holda
.
2-misol. Aniq integralni hisoblang:
Yechish. Aniq integral xossalaridan va Nyuton-Leybnits formulasidan foydalanib,
quyidagi natijaga ega bo‘lamiz:

3 -misol. Aniq integralni hisoblang:
Yechish. almashtirishni bajaramiz. U holda bo‘lib, hosil
bo‘ladigan integral chegaralari va bo‘ladi. U holda (4) formulaga
asosan quyidagiga ega bo‘lamiz:
10

Natijada masala ko‘phadni integrallashga keltirildi:

Shunday qilib,
.
4-misol. Aniq integralni hisoblang:

Yechish. almashtirish bajarsak, quyidagiga ega bo‘lamiz:
2 -§ . Aniq integral yordamida yuzalarni hisoblash
Aytaylik, funksiya oraliqda aniqlangan, uzluksiz va nomanfiy
bo’lsin. U holda funksiya grafigi Ox o‘qining kesmasi, va
to‘g‘ri chiziqlar bilan chegaralangan Φ soha yuzi(1- rasm) quyidagi formula orqali
hisoblanadi:
(6)
1-rasm.
Odatda Φ soha egri chiziqli trapetsiya deb ataladi.
11

Agar funksiya parametrik ko‘rinishda
berilgan bo‘lib, funksiya oraliqda nomanfiy qiymatlarni
qabul qilsin va uzluksiz bo‘lsin. Shuningdek, bo‘lib, funksiya
esa da nomanfiy qiymatlarni qabul qilsin. U holda Φ soha yuzi
(7)
formula bilan hisoblanadi. Aytaylik, va funksiyalar da
uzluksiz bo‘lib, bo‘lsin. U holda va funksiyalar
grafiklari va hamda to‘g‘ri chiziqlar mos kesmalari bilan chegaralangan
Φ soha yuzi (2-rasm) quyidagi formula orqali hisoblanadi:
(8)

2-rasm.
Berilgan funksiyalarga nisbatan yuqoridagiga o‘xshash farazlar asosida, Φ shakl
(3-rasm) yuzasi uchun quyidagi formulalar o‘rinli bo‘ladi:
(6′)
12

(7′)
3-rasm.
Φ shaklining (4-rasm) yuzasi uchun esa:
(8′)
4-rasm.
Aytaylik, oraliqda uzluksiz va nomanfiy funksiya bo‘lsin,
bunda U holda qutb koordinatalarida berilgan funksiya
grafigi hamda mos ravishda va nurlarning kesmalari bilan
chegaralangan Φ sektor yuzasi (5-rasm) quyidagiga teng:
(9)
13

Misollar ishlanishidan namunalar
1-misol. parabola va to‘g‘ri chiziq bilan chegaralangan Φ
shaklning yuzini hisoblang (6-rasm).
Yechish. Berilgan egri chiziqlarning kesishish nuqtalarining abssissalarini
topamiz. Buning uchun

tenglamani yechib, kesishish nuqtalari absissalari va ekanligini
topamiz. U holda (8) formula yordamida shaklning yuzasi quyidagicha
hisoblanadi:
2-misol . ellipsga nuqtada urinma o‘tkazilgan. Egri chiziqli
ABC uchburchakning yuzasini toping (7- rasm ).
14

7-rasm.
Yechish. Ellipsning AC yoyi va urinmaning BC kesmasi quyidagi funksiyalarning
grafiklari hisoblanadi:
h amda
( 8 ) formulaga ko‘ra
funksiyaning integralini bevosita hisoblaymiz:
Shunday qilib, natijani hosil qilamiz.
3-misol. giperbolada nuqta berilgan. OAM egri chiziqli
uchburchakning yuzini toping (8-rasm).
15

8-rasm.
Yechish. formulalar bo‘yicha qutb koordinatalariga o‘tamiz.
U holda giperbolaning tenglamasi quyidagi ko‘rinishga keladi:
OAM uchburchakning yuzasini (9) formula orqali topamiz:
bu yerda Bundan, ekanligini hisobga olsak, quyidagiga ega
bo‘lamiz:
4 -misol. Ushbu
egri chiziq bilan chegaralangan shakl yuzini toping.
16

9-rasm.
Yechish. Egri chiziq (9-rasm) va o‘qlariga nisbatan
simmetrik. Berilgan shaklning birinchi chorakda joylashgan qismining, ya’ni OAB
egri chiziqli uchburchagining yuzini topamiz. Egri chiziqni parametrik tarzda
ifodalaymiz: bunda kesma
egri chiziqning AB yoyiga mos keladi. U holda OAB uchburchakning yuzi (7)
formulaga ko‘ra quyidagiga teng:
(10)
Bu yuzani hisoblashni quyidagicha soddalashtirish mumkin. (10) ga bo‘laklab
integrallash formulasini qo‘llab va ekanilini hisobga olib,
quyidagini tenglikni olamiz:
(11)
(10) va (11) tengliklarni qo‘shsak, quyidagiga ega bo‘lamiz:
(12)
Bundan esa
17

Demak, berilgan shaklning yuzi ga teng.
5-misol . egri chiziq bilan chegaralangan
shaklning yuzini toping (10-rasm).
10-rasm.
Yechish. Aytaylik, bo‘lganda funksiya o‘zining
eng katta qiymati ga erishsin. Egri chiziqning OA quyi yoyi,
funksiyasining grafigi bo‘lib, da ushbu
parametrik formulalar bilan berilgan. Yuqori OA yoyi esa
funksiyasining grafigi bo‘lib, u ya’ni yuqoridagi formulalar bilan
parametrik tarzda berilgan, lekin bu safar shaklning va egri
chiziqli uchburchakning yuzalarini (7) formula yordamida topamiz. Berilgan
shaklning yuzi esa bu yuzalarning ayirmasiga teng:
18

ya’ni
(13)
(13) formula 4-misoldagi (10) formulaga o‘xshash, ammo bu holda qaralayotgan
shakl yopiq egri chiziq bilan chegaralangan. Ko‘pincha (13) tipidagi integrallarni
hisoblashlarni 4-misoldagi kabi soddalashtirish mumkin. (13) ga bo‘laklab
integrallash formulasini qo‘llab va

ekanligini inobatga olib, quyidagi formulaga kelamiz:
(14)
(13) va (14) formulalarni qo‘shib, (12) ga o‘xshash quyidagi
(15)
formulani hosil qilamiz.
Bu holda (15) formula bo‘yicha hisoblashlar (13) yoki (14) formulalarga
qaraganda ancha soddalashadi:
3-§. Egri chiziq yoyi uzunligini hisoblash
Parametrik tenglamalari bilan berilgan ushbu

fazoviy egri chiziqning yoyi uzunligi quyidagi formula orqali hisoblaniladi:
(16)
19

bu yerda da uzluksiz differensiallanuvchi funksiyalar.
Parametrik ko‘rinishda berilgan tekislikdagi egri chiziq yoyining uzunligi esa
quyidagiga formuladan topiladi:
(17)
bu yerda va oraliqda uzluksiz differensiallanuvchi funksiyalar. Agar
tekislikdagi egri chiziq tenglama bilan berilgan bo‘lib,
oraliqda uzluksiz differensiallanuvchi funksiya bo‘lsa, u holda bu chiziqning
oraliqdagi yoyi uzunligi quyidagiga teng bo‘ladi:
(18)
Qutb koordinatalarida tenglama bilan berilgan yassi egri chiziq
yoyining uzunligi esa quyidagiga formula orqali hisoblanadi:
(19)
bu yerda oraliqda uzluksiz differensiallanadigan funksiya. Egri chiziq
yoyining uzunligi ba’zan uning tabiiy parametri deb ataladi. Tekis egri chiziqning
tenglamalar bilan berilishi, egri chiziqning tabiiy
parametrlash deb yuritiladi, bu yerda – egri chiziqning biror nuqtasidan
nuqtasigacha bo‘lgan yoyi uzunligi. Bunda chiziqqa yo‘nalish berilib,
yoylarning shu yo‘nalishdagi nuqtalargacha bo‘lgan uzunliklari musbat, qarama-
qarshi yo‘nalishdagi nuqtalargacha bo‘lgan uzunliklari esa manfiy deb qabul
qilinadi. Egri chiziqning nuqtadagi egrilik radiusi va uning shu nuqtagacha
bo‘lgan yoyi uzunligi s ni bog‘lovchi tenglamani egri chiziqning
tabiiy (ichki) tenglamasi deb ataladi.
1-misol. aylananing yoyi va funksiyaning grafigi bilan
chegaralangan egri chiziqli uchburchakning perimetrini toping.
20

11- rasm .
Yechish. 11- rasmda ko ‘ rsatilgan aylana va funksiya grafigining
kesishish nuqtalari bo ‘ lgan A va B nuqtalarning koordinatalarini topamiz :
Aylananing AB yoyi tenglamasini quyidagi
oshkor ko‘rinishda ifodalaymiz va yoy uzunligi ni (18) formula yordamida
hisoblaymiz:

va yoylarning va uzunliklari bu yoylarning o‘qiga nisbatan
simmetrik ekanligiga ko‘ra o‘zaro teng. OB yoyning uzunligini topamiz. Shartga
ko‘ra u formula bilan berilgan, biroq funksiyaning
hosilasi x = 0 nuqta atrofida chegaralanmagan. Shu sababli, y ni erkli o‘zgaruvchi
sifatida qabul qilib, OB yoyni tenglama bilan ifodalaylik. Bu holda
bo‘ladi va (18) ga o‘xshash formuladan quyidagini olamiz:
Ushbu almashtirishni bajarib, quyidagini natijaga ega bo‘lamiz:
21

Shunday qilib, misolda berilgan uchburchakning perimetri
ga teng.
2-misol. Markazi koordinatalar boshida joylashgan ushbu
astroida yoyini teng uzunlikdagi uchta qismga
bo‘luvchi aylananing radiusini toping.
12-rasm .
Yechish . Astroidaning yoyini ko‘rinishida
parametrlaymiz va (17) formula bo‘yicha ga mos keluvchi) nuqtadan
ga mos keluvchi nuqtagacha bo‘lgan yoy uzunligini hisoblaymiz
(12-rasm):
yoyning to‘liq uzunligi ga teng. AC yoyning uzunligi ga
teng bo‘lishi shartidan ekanligini olamiz, bundan
Astroidaning to‘g‘ri chiziqqa nisbatan simmetrikligiga ko‘ra markazi O va
radiusi bo‘lgan aylana AB yoyni uzunligi bo‘yicha teng uchta yoyga
bo‘ladi.
3 -misol .
22

fazoviy egri chiziq yoyining uzunligini toping
Yechish . Parametr sifatida ni qabul qilamiz. U holda

bo‘ladi va (16) formuladan quyidagini topamiz.

4-misol. ellips yoyi uzunligini elliptik funksiya orqali ifodalang.
Yechish . Birinchi chorakda joylashgan ellips yoyini quyidagicha parametrlaymiz :
Bu yoyning uzunligi quyidagiga teng bo‘ladi:
Ellipsning to‘liq uzunligi esa ga teng bo‘lib, u ni tashkil etadi.
4-§. Aylanish jismlarining hajmlarini hisoblash
Aytaylik, funksiya kesmada uzluksiz va nomanfiy
bo‘lsin. U holda funksiya grafigi, va to‘g‘ri chiziqlarning
kesmalari hamda o‘qining kesmasi bilan chegaralangan shaklni (13-
rasm) o‘qi atrofida aylanishidan hosil bo‘lgan jismning hajmi V
quyidagiga teng:
23

(20)

13-rasm.
Agar funksiya parametrik ko‘rinishda
tenglamalar bilan berilgan bo‘lib, funksiya oraliqda musbat uzluksiz
hosilaga ega va bo‘lsin. Shuningdek, funksiya
oraliqda uzluksiz va musbat bo‘lsa, u holda shaklning (13-rasm) o‘qi atrofida
aylanishidan hosil bo‘lgan jismning hajmi V quyidagiga teng bo‘ladi:
(21)
Agar funksiya kamayuvchi va bo‘lsa, u holda
yuqoridagi shartlar o‘zgarmagan holda shaklning o‘qi atrofida aylanishidan
hosil bo‘lgan jismning hajmi quyidagiga
(21′)
teng bo‘ladi. Aytaylik, va funksiyalari kesmada uzluksiz
va bo‘lsin. , funksiyalarning grafiklari
24

14-rasm. 15-rasm. 16-rasm.
va hamda to‘g‘ri chiziqlarning kesmalari bilan chegaralangan Φ
shaklning (14-rasm) Ox o‘qi atrofida aylanishidan hosil bo‘lgan jismning hajmi
(22)
15-rasm va 16-rasmda ko‘rsatilgan Φ shaklning Oy o‘qi atrofida aylanishidan hosil
bo‘lgan jismlar uchun, berilgan funksiyalarga nisbatan o‘xshash farazlar asosida,
hajmlarni hisoblash uchun mos ravishda quyidagi formulalar qo‘llaniladi:
(23)
(24)
(25)
Jism fazosida tekisliklar orasida joylashgan bo‘lsin.
Jismning o‘qiga perpendikulyar tekislik bilan kesilgan har bir kesimi
yuzaga ega bo‘lsin, bu yerda oraliqda integrallanuvchi funksiya.
Agar bu jism hajmga ega bo‘lsa, uning hajmi quyidagi teng bo‘ladi:
(26)
Agar o‘qi o‘rniga yoki o‘qi olinsa ham, shunga o‘xshash formulalar
o‘rinli bo‘ladi.
25

1 -misol. parabola yoyi, Ox o‘qining kesmasi va to‘g‘ri chiziq
kesmasi bilan chegaralangan shaklni qaraylik. Bu shaklning o‘qi atrofida
aylanishidan hosil bo‘lgan jismning hajmini toping.
Yechish. parabola bilan to‘g‘ri chiziq kesishish nuqtasi C ning
abssissasi ni topamiz (17-rasm): bundan kelib
chiqadi. Izlanayotgan hajm ABCD egri chiziqli trapetsiya va OCD uchburchakning
aylanishidan hosil bo‘lgan va jismlarning hajmlari ayirmasiga teng. (6)
formuladan quyidagilarni topamiz:

Demak, berilgan aylanish jismining hajmi quyidagiga teng:
17-rasm. 18-rasm.
2-misol. aylanani o‘qi atrofida aylantirishdan hosil bo‘lgan
jismning hajmini toping (18-rasm).
Yechish. AOC va ABC yoylar quyidagi funksiyalarning grafiklaridir:
Aylanma jismning hajmini (11) formuladan topamiz:
26

5-§. Sirtlarning yuzalarini hisoblash
Aytaylik, kesmada uzluksiz differensiallanuvchi funksiya
bo‘lsin. Bu funksiya grafigini o‘q atrofida aylantirish natijasida hosil bo‘lgan
sirtning yuzi S quyidagiga formula orqali topiladi:
(27)
Aytaylik, yarim tekislikda egri chiziq ushbu
parametrik tenglamalari bilan berilgan bo‘lsin. Bu yerda va
oraliqda uzluksiz differensiallanuvchi funksiyalar. Berilgan egri chiziqning
o‘qi atrofida aylanishidan hosil bo‘lgan sirtning yuzasi S quyidagi formula
bo‘yicha topiladi:
(28)
Agar egri chiziq yarim tekislikda joylashgan bo‘lsa, u holda quyidagi
formuladan foydalaniladi:
(29)
Yuqoridagiga o‘xshash shartlarda egri chiziqning o‘qi atrofida aylanishidan
hosil bo‘lgan sirtning yuzi mos ravishda quyidagi formulalar orqali hisoblaniladi:
(27′)
(28′)
27

(29′)
Uzunligi bo‘lgan to‘g‘rilanuvchi egri chiziq l to‘g‘ri chiziqning bir tomonida
joylashgan bo‘lsin. - uzunligi s bo ‘ lgan egri chiziq yoyining oxiridan to ‘ g ‘ ri
chiziqqacha bo ‘ lgan masofa va oraliqda uzluksiz funksiya bo ‘ lsin . U
holda bu egri chiziqning to‘g‘ri chiziq atrofida aylanishidan hosil bo‘lgan
sirtning S yuzasi quyidagiga teng:
(30)
egri chiziqning qutb o‘qi atrofida aylanishidan hosil
bo‘lgan sirtning yuzasi esa quyidagiga teng bo‘ladi:
bu yerda oraliqda uzluksiz differensiallanuvchi funksiya. Xuddi shu
shart bajarilganda, egri chiziqning nur atrofida aylanishidan hosil
bo‘lgan sirt yuzi quyidagiga teng bo‘ladi:
bu yerda Silindrik sirtning yasovchilari Oz o‘qiga parallel
bo‘lsin, uning tekislikdagi yo‘naltiruvchisi esa maxsus nuqtalarga ega
bo‘lmagan va quyidagi parametrik tenglamalar bilan berilgan egri chiziq
bo‘lsin:
(31)
28

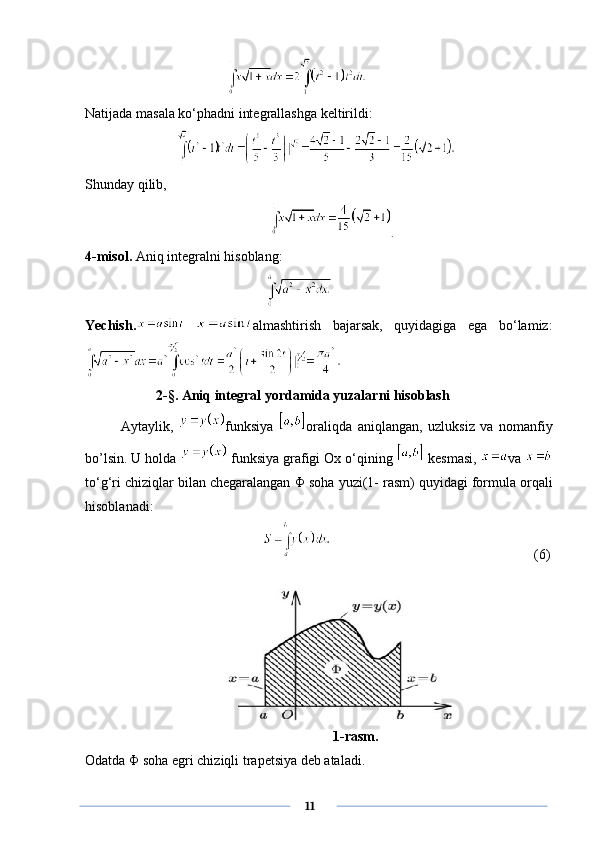
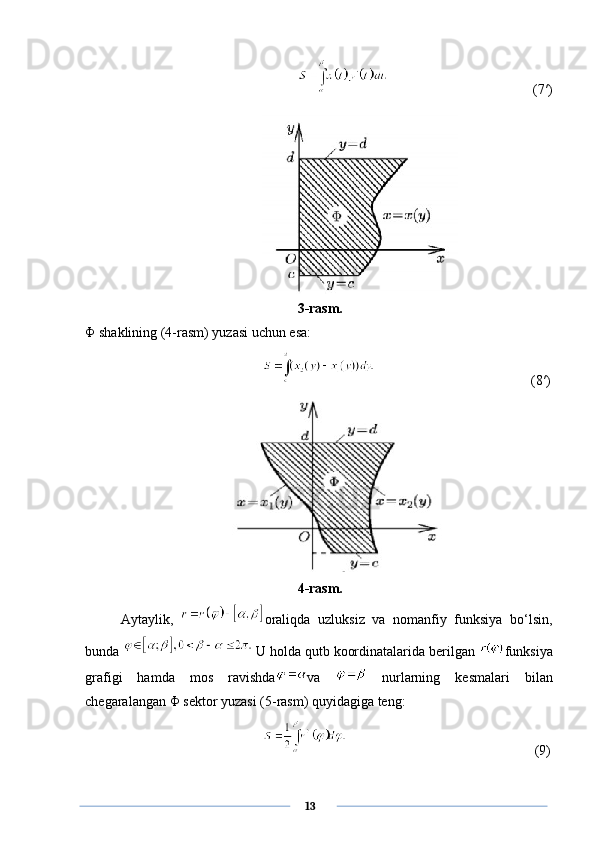
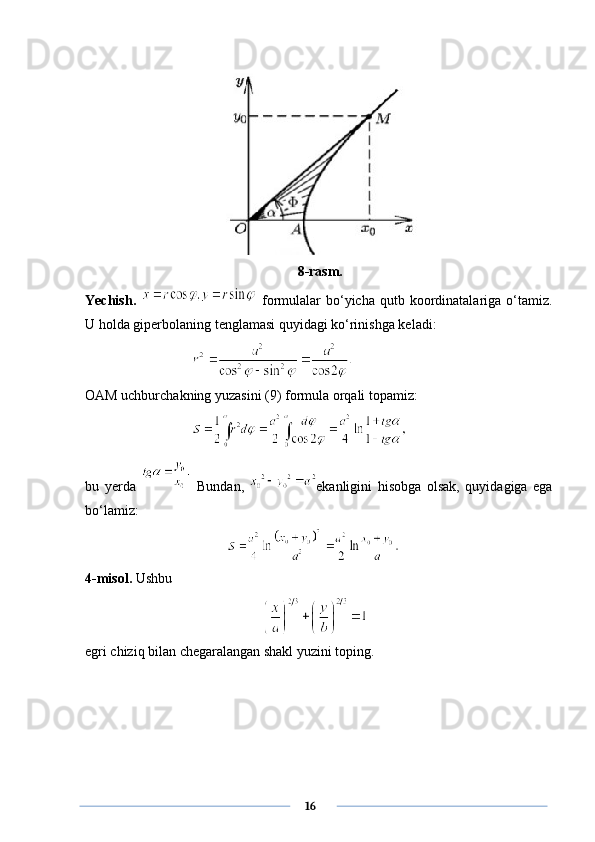
bu yerda x(t) va y(t) - [ α ; β ] oraliqda uzluksiz differensiallanuvchi funksiyalar. Bu
sirtda L egri chiziq (31) va

tenglama bilan parametrik tarzda berilgan bo‘lsin. Bu yerda – manfiy
bo‘lmagan va oraliqda uzluksiz funksiya. Silindrik sirtning va
egri chiziqlar hamda va ga mos keluvchi yasovchilar orasidagi
qismining S yuzasi quyidagiga teng bo‘ladi:
(32)
Agar parametr sifatida egri chiziq yoyining s uzunligi olinsa, u
holda
(33)
agar parametr bo‘lib, shartni qanoatlantirsa, u holda
(34)
Silindrik sirtda ikkita va egri chiziqlar mos ravishda (31) hamda
va
tenglamalar bilan parametrik ko‘rinishda berilgan bo‘lsin, bu yerda va
oraliqda uzluksiz va shartni qanoatlantiradi. Silindrik
sirtning va egri chiziqlar hamda va yasovchilar orasidagi qismining
yuzi quyidagiga teng:
(35)
29

1-misol. parabola yoyining (19-rasm):
1) o‘q
atrofida; 2) o‘q atrofida aylanishidan hosil bo‘lgan sirt yuzini toping.
Yechish.
19-rasm.
1) (27) formuladan quyidagini topamiz:
almashtirish bajaramiz. Agar bo‘lsa, va agar
bo‘lsa, bo‘lishini hisobga olsak, u holda quyidagiga ega bo‘lamiz:
(36)
funksiyaning boshlang‘ich funksiyasi ni topish uchun, masalan,
almashtirishdan foydalanishimiz mumkin. Buning natijasida quyidagini hosil
qilamiz:
30

(36) dan quyidagiga ega bo‘lamiz:
Boshlang‘ich funksiyaning qiymatlarini hisoblaymiz:

U ho lda
natijaga ega bo‘lamiz.
2) Egri chiziqni parametrik ravishda tenglamalar bilan berilgan
deb hisoblab, (28′ ) formuladan quyidagini topamiz:
2-misol. to‘g‘ri chiziq

sikloida yoyini A va B nuqtalarda kesib o‘tadi. Sikloidaning AB yoyi to‘g‘ri
chiziq atrofida aylantirilganda hosil bo‘lgan sirt yuzasini toping (20-rasm).
31

20-rasm.
Yechish. A va B nuqtalar parametrning va qiymatlariga, AB yoyi
esa oraliqqa mos keladi. Aylanish sirtining yuzini quyidagi (28) ga
o‘xshash formula yordamida topamiz:
(37)
Bu yerda (28) dagi egri chiziq nuqtasidan Ox o‘qigacha (aylanish o‘qi) bo‘lgan
masofa o‘rniga, egri chiziq nuqtasidan y = a to‘g‘ri chiziqqacha bo‘lgan
masofa keltirilgan. Bu holda to‘g‘ri chiziq aylanish o‘qi vazifasini
bajaradi (20-rasm).

(37) formuladan quyidagi
tenglikni hosil qilamiz.
almashtirish bajargandan keyin quyidagini topamiz:
32

XULOSA
Matematik analizning asosiy bo‘limlaridan biri bo‘lgan aniq integral
tushunchasi nazariy va amaliy jihatdan nihoyatda muhim hisoblanadi. Ushbu
mavzuni o‘rganish orqali biz matematik vositalarni real hayotdagi geometrik va
fizik muammolarni hal etishda qanday qo‘llash mumkinligini chuqur anglab
yetamiz.Birinchidan, aniq integralning asosiy tushunchalarini o‘zlashtirish, uni
funksiya grafigi ostidagi sath yuzasini aniqlashda ishlatish imkonini beradi. Bu
orqali har xil shakldagi tekislik figuralarining maydonlarini hisoblash
mumkin.Ikkinchidan, aniq integral yordamida egri chiziqli yoy uzunligini
33

hisoblash usullari o‘rganildi. Bu esa geometriyadagi ko‘plab amaliy masalalarda,
xususan, arxitekturaviy tuzilmalar va mexanik tizimlar qurilishida qo‘l
keladi.Uchinchidan, yuzalarni koordinata o‘qlari atrofida aylantirish orqali hosil
bo‘lgan aylanish jismlarining hajmini aniq integral yordamida hisoblash metodlari
o‘rganildi. Bu usullar ko‘plab muhandislik va texnik loyihalarda
qo‘llaniladi.To‘rtinchidan, aylanish jismlarining sirt yuzalarini topish formulasini
o‘zlashtirish orqali yanada murakkab shakllarning tashqi o‘lchamlarini aniqlashga
erishildi.
Xulosa qilib aytganda, aniq integrallarni geometriyada qo‘llash nafaqat
nazariy bilimlarni boyitadi, balki fan va texnikaning turli sohalarida real
masalalarni hal qilishga asos bo‘ladi. Bu mavzu matematik analiz fanining amaliy
ahamiyatini ko‘rsatib beradi va kasbiy sohalarda zarur ko‘nikmalarni
shakllantirishda muhim rol o‘ynaydi.
FOYDALANILGAN ADABIYOTLAR
1. O’zbekiston Respublikasi Prezidentining 2020-yil 7-maydagi “Matematika
sohasidagi ta’lim sifatini oshirish va ilmiy-tadqiqotlarni rivojlantirish chora-
tadbirlari to’g’risida”gi PQ-4708-sonli Qarori.
2.Alimov Sh.O. Ashurov R.R. Matematik analiz 1,2,3 q.T. “ Mumtoz so’z”
2018.
3. G. Xudoyberganov, A. K. Vorisov, X. T. Mansurov, B. A. Shoimqulov.
Matematik analizdan ma’ruzalar 1-qism. T: “Voris-nashriyot” 2010 yil
34

4. B. A. Shoimqulov, T. T. Tuychiyev, D. H. Djumaboyev. Matematik
analizdan mustaqil ishlar. T: “O‘zbekiston faylasuflari milliy jamiyati” 2008
yil.
5. Sadullayev A., Mansurov X.T., Xudoyberganov G., Vorisov A.K., G’ulomov
R. Matematik analiz kursidan misol va masalalar to’plami,1,2,3 q.
T.”O’qituvchi”, 1995,1995,2000.
6. Shokirova X.R Karrali va egri chiziqli integrallar. T.”O’zbekiston”,1990.
7. Canuto C., Tabacco A. Mathematical Analysis, II. Springer-Verlag, Italia,
Milan, 2008.
8. Azlarov T.A., Mansurov X.T. Matematik analiz,1,2
q.T.”O’qituvchi”,1994,1995.
Internet saytlari.
1. http://www.ziyonet.uz/
2. http://www.allniath.ru/
3. http://www.mcce.ru/
4. http://www.mexmat.ru/
5. http://www.webmath.ru/
6. http://www.exponenta.ru/
7. www.lib-homelinex.org/math
8. www.eknigu.com/lib/Mathematics/
35

Aniq integrallarning geometriyaga tatbiqlari

Купить