Differensial hisobning geometriyaga ba’zi bir tatbiqlari - Алгебра - Курсовые работы

Информация о документе

Цена	30000UZS
Размер	823.1KB
Покупки	0
Дата загрузки	11 Июнь 2025
Расширение	docx
Раздел	Курсовые работы
Предмет	Алгебра

Продавец

G'ayrat Ziyayev

Дата регистрации 14 Февраль 2025

87 Продаж

Differensial hisobning geometriyaga ba’zi bir tatbiqlari

Купить

O‘ZBEKISTON RESPUBLIKASI
OLIY TA’LIM FAN VA INNOVATSIYALAR VAZIRLIGI
Farg‘ona davlat universiteti
“Matematik analiz va differensial tenglamalar ” kafedrasi
Kurs ishi
Mavzu: “ Differensial hisobning geometriyaga ba’zi bir tatbiqlari ”
Bajardi: 2-kurs 23.05-guruh talabasi

Ilmiy rahbari: “Matematik analiz va
differensial tenglamalar kafedrasi mudiri;

FARG’ONA-2025

REJA :
Kirish.
ASOSIY QISM
1-§. Funksiya hosilasining ta’rifi.
2-§. Funksiya qavariqligi va botiqligi.
3-§. Funksiyaning egilish nuqtalari va asimptotalari.
4-§. Egri chiziqlarning tekislikda analitik ifodalanishi.
5-§. Yassi egri chiziqqa urinma.
Xulosa.
Foydalanilgan adabiyotlar.
26

KIRISH
“Agar mendan sizni nima qiynaydi?” deb
so‘rasangiz, farzandlarimizning ta’lim
tarbiyasi deb javob beraman!!!
Shavkat Mirziyoyev
Ilg‘or millat va rivojlangan davlat bo‘lishning zarur shartlaridan biri
aqliy va jismoniy, ma’daniy va ma’naviy, axloqiy, g‘oyaviy – siyosiy va
huquqiy jihatdan har tomonlama yetuk, barkamol insonlarga ega bo‘lishdir.
Ma’naviy–ma’rifiy jihatdan inson, inson irodasi mustahkam, e’tiqodi
yuksak, vijdon amri bilan yashaydigan shaxs, barkamol avlod har qanday
davlat, xalq va millatning eng katta boyligi, qudrati salohiyati manbaidir.
Mamlakatimiz prezidenti tomonidan ta’kidlab kelinayotganidek, “Har qaysi
davlat, har qaysi millat nafaqat yerosti va yerusti boyliklari bilan, harbiy
qudrati va ishlab chiqarish salohiyati bilan, balki birinchi navbatda o‘zining
yuksak madaniyati va ma’naviyati bilan kuchlidir”.
Odamlari, fuqarolari bilimli–zakovatli, uddaburon, g‘oyaviy siyosiy
jhatdan ziyrak va hushyor, tadbirkor, har tomonlama yetuk bo‘lgan jamiyat
har qanday islohotlarga qodir bo‘ladi va har qanday muammo va
qiyinchiliklarni yenga oladi. Oliy rahbarimiz bu haqida shunday dedi:
“Lo‘nda qilib aytganda, bugungi kunda oldimizda qo‘ygan buyuk
maqsadlarimizga, ezgu niyatlartimizga erishishimizda jamiyatimizning
yangilanishi, hayotimizning taraqqiyoti va istiqboli amalga oshirayotgan
islohotlarimiz, rejalarimizning samarasi taqdiri bularning barchasi
avvalambor zamon talablariga javob beradigan yuqori malakali, ongli
mutaxassis kadrlar tayyorlash muammosi bilan chambarchas bog‘liqligini
barchamiz anglab yetmoqdamiz.
Shu bilan birga barchamiz yana bir haqiqatni anglab yetmoqdamiz.
Faqatgina chinakam ma’rifatli odam inson qadrini, millat qadriyatlarini, bir
26

so‘z bilan aytganda, o‘zligini aniqlash, erkin va ozod jamiyatda yashash,
mustaqil davlatimizning jahon hamjamiyatida o‘ziga munosib, fidoiylik bilan
kurashishi mumkin”. Mustaqil va erkin fikrlayotgan, ongli yashaydigan, o‘z
haq–huquqlarini yaxshi taniydigan, o‘z kuchi va aqliga ishonadigan,
ma’naviy–axloqiy yetuk barkamol bo‘lgan avlodni, mustaqil fikrlashga qodir,
jasoratli, fidoiy va tashabbuskor kishilarni tarbiyalab yetkazadigan xalq va
millat kelajakka ochiq ko‘z, katta ishonch, umid va ixlos bilan qaray oladi.
Fuqarolarni ana shunday noyob xislat va fazilat sohiblari qilib shakllantirilgan
davlatning istiqboli porloq bo‘ladi.
Kurs ishining dolzarbligi. Differensial hisob elementlari funksiyaning
ma’lum oraliqda o‘zgarmas qiymatni saqlashi, o‘suvchi yoki kamayuvchi
bo‘lishi, maksimum va minimum qiymatlarini toppish, uning grafigining
qavariq yoki botiqligini hamda burilish nuqtalarini aniqlashda muhim
ahamiyat kasb etadi.
Kurs ishining obyekti va predmeti. Kurs ishining obyekti va predmeti
bu differensial tushunchasi, differensial hisobning tadbiqlari
haqidama’lumotlar. Ulardan foydalanish jarayonida turli xil ta’rif, tushuncha
va teoremalardan foydalaniladi. Kurs ishini tayyorlash jarayonida hosila va
uning tadbiqlari o‘rganilib, ularga doir misollar tahlil qilinadi.
Kurs ishining maqsad va vazifalari.
1. Differensial hisobning funksiyani tekshirishda tatbiqlarini o‘rganish
2. Differensial hisobning geometriyaga tatbiqlarini o‘rganish
3. Differensial hisobning elementar matematikaga tatbiqlarini
o‘rganish
Kurs ishining yangiligi va amaliy ahamiyati. Kurs ishi referativ-uslubiy
xarakterga ega bo‘lgani uchun ilmiy yangilik qilinmagan. Mavzuga oid bir
nechta adabiyotlardan ma’lumotlarni to‘plash tahlil qilish va misollarga tatbiq
qilishdan iborat.
26

Tadqiqot usuli va uslubiyoti. Kurs ishi nazariy xarakterga ega bo‘lib,
olingan natijalar boshqa adabiyotlar bilan taqqoslanib mavzuga oid misollarni
yechishda sodda usullar keltirilgan.
Olingan asosiy natijalar. Ish ilmiy xarakterga ega bo‘lmagani sababli
unda alohida ilmiy natija olinmagan. Shunday bo‘lsada ishda keltirilgan
tushunchalar, xossalar, teoremalar va formulalardan ko‘plab masalalarni hal
qilishda foydalanish mumkin. Differensial hisobning tatbiqlariga doir misollar
keltirilgan.

26

1-§. Funksiya hosilasining ta’rifi.
Faraz qilaylik, funksiya da berilgan bo‘lib, ,
bo‘lsin.
Ma’lumki, ushbu

ayirma funksiyanin nuqtadagi orttirmasi deyiladi.
1- ta’rif .Agar ushbu

limit mavjud va chekli bo‘lsa, u f(x ) funksiyaning x nuqtadagi hosilasi⁰
deyiladi va df( x
0 )/dx yoki f '( x
0 ), yoki (f (x))
́ x
0 kabi belgilanadi.
Demak,
(1)
Agar deyilsa, unda va da bo‘lib, (1)
munosabat quyidagi

(2)
ko‘rinishga keladi.
1- misol. bo‘lsin. Bu funksiya uchun

bo‘lib,

bo‘ladi. Demak,
26

2- misol . bo‘lsin.
Agar bo‘lsa, u holda bo‘lib, bo‘ladi.
Agar bo‘lsa, u holda bo‘lib , bo‘ladi.
Agar bo‘lsa, u holda bo‘lib, da bu
nisbatlarning limiti mavjud bo‘lmaydi. Demak, berilgan funksiya
nuqtada hosilaga ega bo lmaydi.ʻ
3- misol. bo‘lsin.
a) uchun

bo‘lib,

bo‘ladi.
b) uchun

bo‘lib,

bo‘ladi.
d) , uchun

bo‘lib,

bo‘ladi. Demak, da .
4- misol . Aytaylik,
26

f(x) { x sin 1
x , agar x ≠ 0 bo ' lsa
0 , agar x = 0 bo ' lsa
bo‘lib, bo‘lsin. Unda

bo‘lib, uning dagi limiti mavjud emas. Demak, berilgan funksiya
nuqtada hosilaga ega emas
Funksiyaning o‘ng va chap hosilalari.
Faraz qilaylik, f(x) funksiya to‘plamda berilgan bo‘lib,
bo‘lsin.
2-ta’rif. Agar ushbu

Limit mavjud bo‘lsa,bu limit f(x) funksiyaning nuqtadagi chap
hosilasi deyiladi va kabi belgilanadi.

Aytaylik f(x) funksiya to‘plamda berilgan bo‘lib,
bo‘lsin.
3-ta’rif . Agar ushbu

limit mavjud bo‘lsa,bu limit f(x) funksiyaning nuqtadagi o‘ng hosilasi
deyiladi va kabi belgilanadi.
.
Masalan, funksiyaning nuqtadagi o‘ng hosilasi
chap hosilasi bo‘ladi.
26

Yuqorida keltirilgan ta’riflardan quyidagi hulosalar kelib chiqadi .
1. Agar f(x) funksiya nuqtada xosilaga ega bo‘lsa, u holda bu
funksiya nuqtada o‘ng xamda chap xo silalarga ega va
tengliklar o‘rinli bo‘ladi.
2. Agar f(x) funksiya nuqtada o‘ng xamda chap
xosilalarga ega bo‘lib, bo‘lsa ,u holda f(x) funksiya
nuqtada xosilaga ega va tengliklar o‘rinli
bo‘ladi.
Hosilaning geometrik hamda mexanik ma’nolari.
Faraz qilaylik, f(x) funksiya da berilgan bo‘lib, nuqta
xosilaga ega bo‘lsin. Bu f(x) funksiyaning grafigi chizmada
tasvirlangan Г egri chiziqni ifodalasin.
1-chizma.
Bu Г chiziqda nuqtalarni olib, ular orqali o‘tuvchi l
kesuvchini qaraymiz.
da l kesuvchi limit xolati
chiziqqa nuqtada o‘tkazilgan urinma deyiladi.
Hosilaga ega bo‘lgan funksiyaning uzluksizligi.
Faraz qilaylik, f(x) funksiya da berilgan bo‘lsin.
Teorema. Agar f(x) funksiya nuqtada chekli xosilaga ega
bo‘lsin, u holda f(x) funksiya nuqtada uzluksiz bo‘ladi.
26

Aytaylik, f(x) funksiya nuqtada chekli xosilaga ega
bo‘lsin. Ta’rifga binoan

ya’ni
da
bo‘ladi.
Endi

deb belgilaymiz.
Ravshanki,
da .
Keyingi tengliklardan topamiz:

Odatda, bu tenglik funksiya ortirmasining formulasi deyiladi. Undan

bo‘lishi kelib chiqadi. Bu f(x) funksiyaning nuqtada uzluksiz ekanini
bildiradi.
Eslatma . Funksiyaning biror nuqtada uzluksiz bo‘lishidan uning shu
nuqtada chekli hosilaga ega bo‘lishi xar doim ham kelib chiqavermaydi.
26

Masalan, funksiya nuqtada uzliksiz, ammo u shu nuqtada
xosilaga ega emas.

26

Hosilani hisoblash qoidalari.
Ikki funksiya yig‘indisi, ayirmasi, ko‘paytmasi va nisbatining
xosilasi. Aytaylik, f(x) va g(x) funksiyalari da berilgan
bo‘lib, nuqtada va xosilalarga ega bo‘lsin. Hosila
ta’rifiga ko‘ra

(1)

(2)
bo‘ladi.
1) funksiya nuqtada xosilaga ega bo‘lib,

bo‘ladi.
2) f unksiya nuqtada xosilaga ega bo‘lib,

bo ‘ ladi .
3) funksiya f unksiya nuqtada xosilaga ega bo ‘ lib ,
bo ‘ ladi .
26

1- natija . Agar funksiya nuqtada xosilaga ega bo ‘ lsa ,
funksiya ( c = const ) nuqtada xosilaga ega bo ‘ lib ,
2-natija. Agar funksiyalar nuqtada xosilalarga
ega bo‘lib, o‘zgarmas sonlar bo‘lsa,u holda
bo‘ladi.
Murakkab funksiyaning xosilasi. Faraz qilaylik, funksiya
to‘plamda funksiya to‘plamda berilgan bo‘lib,
nuqtada xosilaga, nuqtada
xosilaga ega bo‘lsin. U xolda murakkab funksiya nuqtada xosilaga
ega bo‘lib,
bo‘ladi.
Teskari funksiyaning xosilasi. Aytaylik, funksiya da
berilgan, uzluksiz va qat’iy o‘suvchi ( qat’iy kamayuvchi) bo‘lib,
nuqtada xosilaga ega bo‘lsin.U xolda funksiya
nuqtada xosilaga ega va
bo‘ladi.
Asosiy teoremalar.
Hosilaga ega bo‘lgan funksiyalar xaqidagi teoremalar. Bu teoremalar
funksiyalarni tekshirishda muhim rol o‘ynaydi.
26

1-teorema (Ferma teoremasi). funksiya to‘plamda berilgan.
nuqtaning atrofi uchun bo‘lib,
quyidagi shartlar bajarilsin:
1) da
2) mavjud va chekli bo‘lsin.
U holda
2-teorema (Roll teoremasi). Faraz qilaylik, funksiya da
berilgan
bo‘lib, quyidagi shartlarni bajarsin:
1)
2)
3) bo‘lsin.
U holda shunday nuqta topiladiki, bo‘ladi.
3-teorema (Lagranj teoremasi). Faraz qilaylik, funksiya da
berilgan bo‘lib, quyidagi shartlarni bajarsin:
1)
2) da xosila mavjud va chekli bo‘lsin.
U holda shunday nuqta topiladiki,

bo ‘ ladi .
1- natija . Aytaylik , funksiya da xosilaga ega bo ‘ lib ,
da bo ‘ lsin . U holda da bo‘ladi.
2-natija. va funksiyalari da , xosilalarga ega
bo‘lib, da bo‘lsin. U holda da
bo‘ladi.
26

4-teorema (Koshi teoremasi). Aytaylik, va funksiyalar
quyidagi shartlarni bajarsin.
1)
2) va xosilalar mavjud va chekli;
3) da bo‘lsin.
U holda shunday nuqta topiladiki,
bo‘ladi.

Funksiya xosilasining uzilishi haqida. Faraz qilaylik, funksiya
ning nuqtasidan boshqa barcha nuqtalarida xosilaga ega bo‘lib
funksiya nuqtada uzluksiz bo‘lsin.
Agar limit ma vjud bo’lsa, u holda funksiya nuqtada
chap hosila ga ega bo‘lib, bo‘ladi.
Agar limit mavjud bo‘lsa, u holda funksiya nuqtada
o‘ng hosila ga ega bo‘lib, bo‘ladi.
2-§. Funksiyaning qavariqligi va botiqligi.
Funksiyaning hosilasi yordamida uning qavariqligi hamda botiqligini
tekshirish mumkin.
funksiya (a,b) intervalda aniqlangan bo‘lib, bu intervalda chekli f ' (
x )
hosilaga ega bo‘lsin.
1-teorema. funksiya ( a , b )
intervalda qavariq (qat’iy qavariq)
bo‘lishi uchun uning
f'(x) hosilasining ( a , b )
da o‘suvchi (qat’iy o‘suvchi)
bo‘lishi zarur va yetarli.
26

Isbot. Zarurligi. funksiya (a,b) da qavariq bo‘lsin. Demak,
∀ x
1 ∈
( a , b ) , ∀ x
2 ∈ ( a , b ) , x
1 < x
2 bo‘lganda ∀ x∈(x1,x2) lar uchun
f(x)≤ x2− x
x2− x1
f(x1)+ x− x1
x2− x1
f(x2)
bo‘ladi,va undan quyidagini topamiz:
f
( x ) − f ( x
1 )
x − x
1 ≤ f ( x
2 ) − f ( x )
x
2 − x . ( 3 )
Shu (3) tengsizlikda avval
x→ x1 da, so‘ng x→ x2 da limitga o‘tsak, u
holda
f '
(
x
1 ) = lim
x → x
1 f
( x ) − f ( x
1 )
x − x
1 ≤ lim
x → x
1 f ( x
2 ) − f ( x )
x
2 − x = f ( x
2 ) − f ( x
1 )
x
2 − x
1 ,
f '
(
x
2 ) = lim
x → x
2 f
( x ) − f ( x
2 )
x − x
2 ≥ lim
x → x
2 f ( x ) − f ( x
1 )
x − x
1 = f ( x
2 ) − f ( x
1 )
x
2 − x
1
bo‘lib, natijada quyidagi
f '
(
x
1 ) ≤ f ( x
2 ) − f ( x
1 )
x
2 − x
1 ≤ f ' ( x
2 )
tengsizliklar kelib chiqadi. Demak,
f'(x1)≤ f'(x2). Shunday qilib, x1<x2
bo‘lganda
f'(x1)≤ f'(x2) bo‘ladi. Bu esa ( a , b )
intervalda f'(x) ning o‘suvchi
ekanini bildiradi. Endi funk siya
(a,b) intervalda qat’iy qavariq bo‘lsin.
Bu holda (3) tengsizlik ushbu
f
( x ) − f ( x
1 )
x − x
1 < f ( x
2 ) − f ( x )
x
2 − x ( 4 )
ko‘rinishda bo‘ladi.
Lagranj teoremasiga ko‘ra
f(x)− f(x1)
x− x1
= f'(ξ1),x1<ξ1<x
f(x2)− f(x)
x2− x = f'(ξ2),x<ξ2<x2
bo‘ladi. So‘ngra
x
1 < ξ
1 bo‘lganda f '
( x
1 ) ≤ f ' (
ξ
1 ) ,
ξ
2 < x
2 bo‘lganda f '
(
ξ
2 ) ≤ f ' (
x
2 )
tengsizlik o‘rinli bo‘lishini hamda (4) tengsizlikni e’tiborga olib topamiz:
26

f'(x2)≥ f'(ξ2)> f'(ξ1)≥ f'(x1). Demak, f '
(
x
1 ) < f ' (
x
2 ) .
Shunday qilib, x
1 < x
2 bo‘lganda
f'(x1)< f'(x2)
bo‘ladi. Bu funksiyaning qat’iy o‘suvchiligini anglatadi.
Yetarliligi. f
( x )
funksiya ( a , b )
intervalda chekli f'(x) hosilaga ega bo‘lib,
u o‘suvchi (qat’iy o‘suvchi) bo‘lsin. Demak,
∀ x1∈(a,b),∀ x2∈(a,b) uchun
x
1 < x
2 bo‘lganda f '
(
x
1 ) ≤ f ' (
x
2 ) ( f ' (
x
1 ) < f ' (
x
2 ) )
tengsizlik o‘rinli. Yana Lagranj
teoremasidan foydalanib topamiz:
f
( x ) − f ( x
1 )
x − x
1 = f ' (
ξ
1 )( x
1 < ξ
1 < x ) , ( 5 )
f
( x
2 ) − f ( x )
x
2 − x = f ' (
ξ
2 )( x < ξ
2 < x
2 ) . ( 6 )
bunda

x1<ξ1<x<ξ2<x2(7)
Demak, ξ
1 < ξ
2 bo‘lganda f '
(
ξ
1 ) ≤ f ' (
ξ
2 ) ( f ' (
ξ
1 ) > f ' (
ξ
2 ) )
tengsizlik o‘rinli
bo‘ladi. U holda (5) va (6) munosabatlardan
f(x)− f(x1)
x− x1
≤ f(x2)− f(x)
x2− x (f(x)− f(x1)
x− x1
< f(x2)− f(x)
x2− x )
bo‘lishi kelib chiqadi. Shunday qilib,
∀ x1∈(a,b),∀ x2∈(a,b) va x1<x2
bo‘lganda (bu holda (7) ga ko‘ra ξ
1 < ξ
2 bo‘ladi)
f
( x ) − f ( x
1 )
x − x
1 ≤ f ( x
2 ) − f ( x )
x
2 − x
( x
1 < x < x
2 ) ,
(
f(x)− f(x1)
x− x1
< f(x2)− f(x)
x2− x )(x1<x<x2)
tengsizliklar o‘rinli bo‘ladi. Natijada (1), (2) va (3) munosabatlarni e’tiborga
olib, funksiyaning
(a,b) intervalda qavariq (qat’iy qavariq) ekaniga
ishonch hosil qilamiz. Teorema isbot bo‘ldi.
Xuddi shunga o‘xshash quyidagi teorema ham isbotlanadi.
2-teorema. funksiya
(a,b) intervalda botiq (qat’iy botiq) bo‘lishi
uchun uning f ' ( x )
hosilasining ( a , b )
da kamayuvchi (qat’iy kamayuvchi)
bo‘lishi zarur va yetarli.
26

Funksiyaning qavariqligi hamda botiqligini uning ikkinchi tartibli
hosilasidan (agar u mavjud bo‘lsa) foydalanib tekshirish mumkin.
funksiya (a,b) intervalda aniqlangan bo‘lib, shu intervalda u ikkinchi
tartibli f ' ' ( x )
hosilaga ega bo‘lsin. Bundan tashqari,
(a,b) intervalning har
qanday
(α,β)((α,β)⊂(a,b),α≠β)¿ qismida f ' ' ( x )
aynan nolga teng bo‘lmasin.
3-teorema. funksiya ( a , b )
intervalda qavariq (botiq) bo‘lishi uchun
shu intervalda
f ' '
(
x ) ≥ 0 ( f ' ' (
x ) ≤ 0 )
tengsizlik o‘rinli bo‘lishi zarur va yetarli.
Isbot. Zarurligi. funksiya
( a , b )
intervalda qavariq (botiq) bo‘lsin. U
holda yuqorida keltirilgan teoremalarga ko‘ra funksiyaning
f'(x) hosilasi
(a,b)
intervalda o‘suvchi (kamayuvchi) bo‘ladi. Funksiyaning monoton
bo‘lishi haqidagi teoremaga ko‘ra f ' '
(
x ) ≥ 0 ¿
bo‘lishini topamiz.
Yetarliligi. Endi
(a,b) intervalda funksiyaning ikkinchi tartibli hosilasi
uchun ushbu f ' '
(
x ) ≥ 0 ( f ' ' ( x ) ≤ 0 )
tengsizlik o‘rinli bo‘lsin. U holda yana
funksiyaning monotonligi haqidagi teoremaga ko‘ra f '
( x )
hosila
(a,b)
intervalda o‘suvchi (kamayuvchi) bo‘ladi. Bundan 3-teoremaga asosan
funksiyaning
(a,b) intervalda qavariq (botiq) bo‘lishi kelib chiqadi. Teorema
isbot bo‘ldi.
1-misol.
f(x)=ln x(x>0) bo‘lsin. Bu funksiya uchun f ' ' (
x ) = − 1
x 2 bo‘lib,
f ' ' ( x ) < 0
bo‘ladi. Demak, f
( x ) = ln x
funksiya ( 0 , + ∞ )
intervalda qat’iy botiqdir.
Shunga o‘xshash, f
( x ) = − ln x , x > 0
funksiya ( 0 , + ∞ )
intervalda qavariq bo‘ladi.
Ushbu f
( x ) = ln x
funksiyaning botiqligidan bitta tengsizlikni keltirib
chiqaramiz. Funksiyaning botiqligi ta’riflaridan x
1 ∈
( 0 , + ∞ ) , x
2 ∈ ( 0 , + ∞ )
lar
uchun x
1 < x
2 va α
1 ≥ 0 , α
2 ≥ 0 , α
1 + α
2 = 1
bo‘lganda quyidagi
α1ln x1+α2ln x2≤ln (α1x1+α2x2)
tengsizlik o‘rinli bo‘ladi. Keyingi tengsizlikni quyidagi
x1α1× x2α2≤α1x1+α2x2
26

ko‘rinishda yozish mumkin. Xususiy holda, α
1 = α
2 = 1
2 bo‘lsa, bundan bizga
ma’lum bo‘lgan√x1× x2≤ x1+x2
2
tengsizlik kelib chiqadi.
3-§. Funksiyaning egilish nuqtalari va asimptotalari.
Funksiya hosilasi yordamida uning egilish nuqtalarini topish mumkin.
funksiya
x0 nuqtaning U δ(x0) atrofida aniqlangan bo‘lsin.
1-ta’rif. Agar funksiya U
δ− ¿ ( x
0 ) ¿
oraliqda qavariq (botiq) bo‘lib,
U δ+¿(x0)¿
oraliqda esa botiq (qavariq) bo‘lsa, u holda x
0 nuqta funksiyaning (funksiya
grafigining) egilish nuqtasi deb ataladi.
f ( x )
funksiya U
δ ( x
0 )
da ikkinchi tartibli f ' ' ( x )
hosilaga ega bo‘lsin. Agar

∀ x∈U δ−¿(x0)¿ uchun f ' ' (
x ) ≥ 0 ( f ' ' (
x ) ≤ 0 ) ,
∀ x ∈ U
δ+ ¿ ( x
0 ) ¿
uchun f ' ' ( x ) ≤ 0
( f ' ' (
x ) ≥ 0 ) .
tengsizlik o‘rinli bo‘lsa, u holda U
δ− ¿ ( x
0 ) ¿
da
f'(x) o‘suvchi (kamayuvchi),
U
δ+ ¿ ( x
0 ) ¿
da f ' ( x )
kamayuvchi (o‘suvchi) bo‘lib,
f'(x) funksiya x0 nuqtada
ekstremumga erishadi. U holda
x0 nuqtada f ' ' (
x ) = 0
bo‘ladi.
Demak,
f(x) funksiyaning egilish nuqtasida ikkinchi tartibli hosila f ' ' ( x )
nolga teng bo‘ladi.
1-misol.
f(x)=e−x2 bo‘lsin. Bu funksiyaning ikkinchi tartibli hosilasi
f''(x)=2e−x2(2x2+1)
bo‘lib, u faqat x = ±
√ 2
2 nuqtalarda nolga aylanadi:
f ' '
( −
√ 2
2
) = 0 f ' ' (
√ 2
2
) = 0
Ravshanki, bu funksiyaning ikkinchi tartibli hosilasi
f''(x)(− ∞ ,− √2
2 ) va
(
√ 2
2 , + ∞ )
intervallarda f''(x)>0 ; [
− √2
2 ,√2
2 ] segmentda esa f ' ' (
x ) ≤ 0.
26

Demak,
f( x ) = e − x 2
funksiya ( − ∞ , − √ 2
2 )
intervalda qavariq,
[
− √2
2 ,√2
2 ]
segmentda botiq va
(√2
2 ,∞) intervalda yana qavariq bo‘ladi. Funksiya
grafigining
(
−√2
2 ,e
−12),B¿ , e
−12¿ nuqtalari uning egilish nuqtalaridir.
Funksiya grafigining asimptotalari.
funksiya a ∈ R
nuqtaning biror atrofida aniqlangan bo‘lsin.
2-ta’rif. Agar ushbu
limx→a+0f(x),limx→a−0f(x)
limitlardan biri yoki ikkalasi cheksiz bo‘lsa, u holda
x=a to‘g‘ri chiziq
funksiya grafigining vertikal asimptotasi deb ataladi.
Masalan, 1
x funksiya grafigi uchun
x=0 to‘g‘ri chiziq vertikal asimptota
bo‘ladi.
Endi y = f ( x )
funksiya ( a , ∞ ) (
( − ∞ , a ) )
oraliqda aniqlangan bo‘lsin.
3-ta’rif. Agar shunday o‘zgarmas k
va b
sonlar mavjud bo‘lsaki,

x=+∞(x→ − ∞) da funksiya ushbu
f
( x ) = kx + b + α ( x )
ko‘rinishda ifodalansa (bunda lim
x → ∓ ∞ α
( x ) = 0 ¿ ¿
, u holda y= kx +b to‘g‘ri chiziq
funksiya grafigining og‘ma asimptotasi deb ataladi.
Masalan,
f
( x ) = x 2
− 3 x − 2
x + 1
bo‘lsin. Bu funksiyani
f
( x ) = x − 4 + 2
x + 1
ko‘rinishda yozish mumkin. Demak,
x→ ±∞ da α(x)= 2
x+1→ 0 bo‘lib, berilgan
funksiya
f(x)= x−4+α(x) ko‘rinishda ifodalanadi. Bundan esa y = x − 4
to‘g‘ri
chiziq funksiya grafigining og‘ma asimptotasi ekani kelib chiqadi.
26

1-teorema. funksiya grafigi y = kx + b
og‘ma asimptotaga ega bo‘lishi
uchun
lim
x → + ∞ f ( x )
x = k , lim
x → + ∞[ f ( x ) − kx ] = b
limitlarning o‘rinli bo‘lishi zarur va yetarli.
Isbot. Zarurligi. funksiya grafigi y = kx + b
og‘ma asimptotaga ega
bo‘lsin. Og‘ma asimptota ta’rifiga ko‘ra
f(x)= kx +b+α(x)
bo‘lib, bunda
x→ +∞ da α ( x ) → 0
bo‘ladi. U holda quyidagilarga egamiz:
lim
x → + ∞ f ( x )
x = lim
x → + ∞ kx + b + α ( x )
x = lim
x → + ∞
[ k + b
x + α ( x )
x ] = k ,
limx→+∞[f(x)− kx ]= limx→+∞[b+α(x)]= b
Yetarliligi. Ushbu
lim
x → + ∞ f ( x )
x = k , lim
x → + ∞
[ f ( x ) − kx ] = b
limitlar o‘rinli bo‘lsin. U holda
limx→+∞[f(x)− kx ]=b
dan f(x)− kx −b=α(x)→ 0 kelib chiqadi. Demak, x→ +∞ da
f(x)= kx +b+α(x)
bo‘lib, lim
x → + ∞ α
( x ) = 0
bo‘ladi. Bu esa y= kx +b to‘g‘ri chiziq funksiya
grafigining asimptotasi ekanini bildiradi. Teorema isbot bo‘ldi.
Funksiyalarni tekshirish. Grafiklarni yasash.
Funksiyalarni tekshirish va ularning grafiklarini yasashni quyidagi sxema
bo‘yicha olib borish maqsadga muvofiqdir:
1. Funksiyaning aniqlash to‘plamini topish;
2. Funksiyani uzluksizlikka tekshirish va uzilish nuqtalarini topish;
3. Funksiyaning juft, toq hamda davriyligini aniqlash;
4. Funksiyani monotonlikka tekshirish;
5. Funksiyani ekstremumga tekshirish;
6. Funksiya grafigining qavariq hamda botiqligini aniqlash, egilish
nuqtalarini topish;
26

7. Funksiya grafigining asimptotalarini topish;
8. Funksiyaning haqiqiy ildizlarini (agar ular mavjud bo‘lsa, shuningdek
argument x ning bir nechta xarakterli qiymatlarida funksiyaning
qiymatlarini yasash.
2-misol. Ushbu
f
( x ) = x 2
− 1
x 2
+ 1
funksiyani tekshiring va grafigini yasang.
Berilgan funksiya R = ( − ∞ , + ∞ )
intervalda aniqlangan va uzluksiz. Bu
funksiya uchun f
( − x ) = f ( x )
tenglik o‘rinli. Demak, juft funksiya (uning
grafigi Oy
o‘qiga nisbatan simmetrik bo‘ladi), uni
[0,+∞ ¿ oraliqda tekshirish
yetarli.
Funksiyaning birinchi va ikkinchi tartibli hosilalarini topamiz:

f'(x)= 4x
(x2+1)2,f''(x)= 4(1−3x2)
(x2+1)3 .
Funksiyaning birinchi tartibli hosilasi
[ 0 , + ∞ ¿
oraliqda mavjud va x=0
nuqtada nolga aylanadi. Shu x = 0
nuqtada ikkinchi tartibli hosilasini
hisoblaymiz. f ' '
(
0) = 4 > 0.
Bundan berilgan funksiya x = 0
da minimumga
ega va
[ 0 , + ∞ ¿
da min f ( x ) = − 1
bo‘ladi. Endi x>0 da f ' ( x ) > 0
bo‘lganidan
berilgan funksiyaning
[0,+∞¿ oraliqda o‘suvchiligini topamiz. So‘ngra ushbu
k = lim
x → + ∞ f ( x )
x = lim
x → + ∞ x 2
− 1
x 2
+ 1 × 1
x = 0 ,
b = lim
x → + ∞ ⌈ f
( x ) − kx ⌉ = lim
x → + ∞ x 2
− 1
x 2
+ 1 = 1
limitlarga ko‘ra y = 1
gorizontal to‘g‘ri chiziq funksiya grafigining
asimptotasi ekaniga va
f
( x ) − 1 = x 2
− 1
x 2
+ 1 − 1 = − 2
x 2
+ 1 < 0
tengsizlikka ko‘ra funksiya grafigi asimptotadan pastda joylashgan bo‘lishiga
ishonch hosil qilamiz.
26

Funksiyaning ikkinchi tartibli hosilasi [0,+∞¿ oraliqning x = 1 √
3 nuqtasida
nolga aylanadi. Ravshanki, 0 < x < 1
√
3 da f ' '
(
x ) > 0 , 1
√
3 < x < + ∞
da f ' ' (
x ) < 0.
Demak,
funksiya ( 0 , 1
√
3 )
intervalda qavariq, ( 1 √
3 , + ∞ )
intervalda botiq bo‘ladi.
x = + 1
√
3 nuqta funksiya grafigining egilish nuqtasidan iborat. Berilgan
funksiyaning grafigi a
chizmada tasvirlang
2-chizma
4- §. Egri chiziqlarning tekislikda analitik ifodalanishi.
Avvalo egri chiziqlarning tekislikda turli usullar bilan ifodalanishi bizga
analitik geometriyadan ma’lum, bunda koordinatalarning to‘g‘ri burchakli
biror sistemasi asos qilib olinadi.
1. Biz yuqorida bir necha marta
y = f
( x )
yoki [x= g(y)] (8)
shakldagi tenglama bilan ish ko‘rgan edik. Egri chiziq nuqtasining
o‘zgaruvchi koordinatalaridan birini ikkinchisining bir qiymatli funksiyasi
sifatida aniqlab berish usuli, egri chiziqni oshkor ravishda berilishi
(tasvirlanishi) deb ataladi. Bunday tasvirlanish soddalik va ayonlik
xususiyatlariga egadir.
Misol tariqasida parabolani olish mumkin:
y= ax2,
26

2. Analitik geometriyada egri chiziq ko‘pincha x ga nisbatan ham, y ga
nisbatan ham yechilmagan.

F(x,y)=0(9)
tenglama bilan beriladi. Bu tenglama egri chiziqning oshkormas tenglamasi
deyiladi.
1-masala. Ellips:

x2
a2+x2
b2−1=0
Ayrim hollarda (9) tenglamadan o‘zgaruvchilardan birini ikkinchisi orqali
ifodalash mumkin, masalan, uni
x orqali ifodalab, egri chiziqni (yoki uning
bir qismini) oshkor shakldagi (8) tenglama bilan ifodalab bo‘ladi. Chunonchi
ellips berilgan holda:
y = ± b
a
√ a 2
− x 2
(− a≪x≪a)
uchun. Boshqa hollarda garchand y ning x
ga bog‘lanishi (9)
tenglama bilan aniqlangan bo‘lsa ham, shu bilan birga, ma’lum shartlar
bajarilganda (9) tenglamani qanoatlantiruvchi bir qiymatli (8) funksiya
mavjud bo‘lib, hatto bu oshkormas funksiya uzluksiz hosilaga ega bo‘lsa ham,
biroq biz uning oshkor ifodasini yoza olmaymiz. Masalan, dekart yaprog‘ini
olganda ahvol shunday bo‘ladi:
x 3
+ y 3
− 3 axy = 0 ¿ chizma)
3-chizma
3. Nihoyat, o‘zgaruvchi koordinatalarning biror parametrga bog‘lanishini
aniqlovchi
26

x=φ(t)y=ψ(t)(10 )
tenglamalar ham tekislikda egri chiziqni aniqlashini bilamiz. Bunday
tenglamalarni parametrik tenglamalar deyiladi; ular egri chiziqning
parametrik tasvirini beradi.
Bunga avvalo ellipsning parametrik shaklda tasvirlanishi misol bo‘la oladi:

x=acos t,y= bsin t,
t
parametrning 0 dan 2π gacha o‘zgarishida katta o‘qning A ( a , 0 )
uchidan
boshlab soat strelkasiga teskari yo‘nalishda ellips chizila boradi ( t
parametrning geometrik ma’nosi (4-chizmada ko‘rinadi).
4-chizma
Ikkinchi misol sifatida sikloidani aytib o‘tamiz:
x = a
( t − sin t ) y = a ( 1 − cos t ) ;
U to‘g‘ri chiziq bo‘ylab g‘ildirab boruvchi doira nuqtasining trayektoriyasi
bo‘ladi (5-chizma). Parametr sifatida qo‘zg‘aluvchi
DM radius bilan uning
boshlang‘ich
OA vaziyati orasidagi burchak olingan: t = ∡ NDM
. t
ning 0 dan
2π
gacha o‘zgarishida nuqta chizmada tasvirlangan yoyni chiza boradi. t ning
− ∞
dan +
∞ gacha o‘zgarishiga mos kelgan butun egri chiziq shunday
yoylarning son sanoqsiz to‘plamidan iborat.
26

5-§. Yassi egri chiziqqa urinma.
Urinma tushunchasi bir necha marta bizga uchragan edi.
y = f( x )
tenglama bilan berilgan chiziq o‘zining har bir ( x , y )
nuqtasida, burchak
koeffitsienti
tan α= y'x= f'(x)
formula bilan ifoda etiladigan urinmaga ega. Demak, urinma, ushbu tenglama
bilan ifodalanadi:
Y − y = y '
x
( X − x )( 11 )
Bunda
X , Y o‘zgaruvchi koordinatalarni, x,y esa urinish nuqtasining
koordinatalarini bildiradi.
Normalning ham, ya’ni urinish nuqtasidan o‘tib, urinmaga tik bo‘lgan
to‘g‘ri chiziq tenglamasini ham hosil qilish oson:
Y − y = − 1
y '
x ( X − x )
yoki

X− x+y'x(Y− y).(12 )
Urinma va normal munosabati bilan, ba’zi kesmalar, ya’ni
MT va MN
kesmalar va ularning x
o‘qqa bo‘lgan TP
va PN
proyeksiyalari ham qaraladi
(6-chizma).
6-chizma
26

TP kesma urinma osti deb, PN esa normal osti deb ataladi. Ularni
tegishlicha sbt
(subtangens) va
sbn (subnormal) orqali belgilanadi.; (11) va
(12) tenglamalarda
Y=0 faraz qilib ushbularni chiqarish oson:
sbt = TP = y
y '
x , sbn = PN = y y '
x ( 13 )
1) Masalan,
y= ax2 parabola uchun:
sbt = y
y '
x = a x 2
2 ax = x
2
Endi bu chiziqning (9) oshkormas tenglama bilan berilish holiga o‘taylik.
Agar bu tenglama bizni qiziqtirgan nuqta atrofida (8) tenglamaga teng kuchli
deb faraz qilinsa, u holda egri chiziq bu nuqtada albatta (11) urinmaga ega.
Bizga bevosita berilmagan “oshkormas” funksiyaning
y'x hosilasini berilgan
F '
X va F '
y hosilalar quyidagicha ifodalanadi:
y'x= − F'X(x,y)
F'y(x,y) ,
bunda
F'y≠0 deb faraz qilinadi. (Bu shart bajarilganda egri chiziqning
qaralayotgan nuqtasi atrofida (9) tenglama (8) tenglamaga teng kuchli
bo‘ladi.)

y'x ning topilgan ifodasini urinma tenglamasiga qo‘ysak, sodda
almashtirishlardan keyin, ushbu tenglamani hosil qilamiz:

F'x(x,y)(X− x)+F'y(x,y)(Y− y)=0(14 )
Bu tenglama x
va
y ga nisbatan to‘la simmetrik bo‘lgani uchun F '
x ≠ 0
shartda
x bilan y ning rollari almashtirilsa, urinma uchun xuddi yana (14)
tenglamaning o‘zi kelib chiqadi. Qaralayotgan holda faqat ikkala
F'x,F'y
hosilalar birdaniga nolga aylansa, (14) tenglik ayniyatga aylanib, aniq to‘g‘ri
chiziq tenglamasi bo‘lmaydi. Bunday holda ( x , y )
nuqtani egri chiziqning
maxsus nuqtasi deyiladi; maxsus nuqtada egri chiziq aslida aniq urinmaga ega
bo‘lmasligi mumkin.
1-misol. 1).Parabola
y 2
= 2 px (7-chizma)
26

7-chizma
Bu tenglikni y ni x
ning funksiyasi deb hisoblab, differensiallaymiz.:
y'x= p
. Shunday qilib: parabolaning urinma osti o‘zgarmas miqdordir.Bundan
parabolaga normal o‘tkazish uchun sodda usul hosil bo‘ladi. Aytilganidek, bu
holda urinma osti juda sodda ifodalanadi-parabola tenglamasini hozirgina
hosil qilingan tenglikka hadma-had bo‘lsak, darhol topamiz:
y
y '
x = 2 x
yoki sbt = 2 x
2) Ellips: x 2
a 2 + y 2
b 2 = 1
(8-chizma)
8-chizma
(14) formulaga asosan, urinma tenglamasi:
x
a 2
( X − x ) + y
b 2 ( Y − y ) = 0
26

Ellips tenglamasini e’tiborga olib, oxirgi tenglamani soddaroq ko‘rinishda
yozish mumkin:
xX
a 2 + yY
b 2 = 1
Bu yerda Y = 0
faraz etib, X = a 2
x ni topamiz. Demak, urinmaning x
o‘q
bilan kesishgan T
nuqtasi y va b
ga bog‘liq emas. Turli b
qiymatlarga javob
beruvchi ellipslarning umumiy
x absissaga ega bo‘lgan nuqtalaridagi hamma
urinmalari x
o‘qdagi bitta T
nuqtadan o‘tadi; b = a
aylana hosil bo‘lib, uning
urinmasi sodda yasalgani uchun
T darhol aniqlanadi, bundan esa ellipsga
urinma yasash usuli kelib chiqadi; yasash usuli 8-chizmada ravshan
ko‘rsatilgan.
3)
x2+y2−3axy =0 bilan ifodalangan dekart yaprog‘I uchun
tenglamaning chap tomonidan olingan ikkala xususiy hosila
3(x2−ay ) va 3(
y2− ax ¿
koordinata boshida bir vaqtda nolga aylanadi, 1-chizmadan ko‘rinib
turibdiki, bu maxsus nuqtada, haqiqatan ham, aniq urinma yo‘q.
Nihoyat, (10) parametrik tenglamalar bilan berilgan egri chiziqni
qaraylik. Tanlab olingan nuqtada
x't = φ'(t) hosila noldan farqli, masalan,
noldan katta bo‘lsa, u shu nuqta atrofida ham musbat bo‘ladi; demak,
x=φ(t)
funksiya monoton o‘sadi, bu holda
t ham x ning o‘suvchi funksiyasi bo‘ladi:
t = t ( x )
, bu funksiyaning hosilasi t '
x = 1
x ' t . Endi t
o‘rniga x
ning bu funksiyasini
y = ψ ( t )
tenglamaga qo‘ysak, egri chiziqning qandaydir bo‘lagida
yx ning
funsiyasi sifatida aniqlanadi:
y = ψ
( t( x )) = f ( x ) ;
bu oxirgi f ( x )
funksiya ham hosilaga egadir. Shunday qilib, egri chiziqning
olingan nuqtaga yondoshuvchi kesmasi (bo‘lagi) oshkor tenglama bilan
ifodalanishi mumkin: bu holda egri chiziq shu nuqtada urinmaga ega bo‘ladi.
Urinmaning burchak koeffisienti quyidagicha ifodalanishi mumkin:
26

tan α= y'x= dy
dx =
dy
dt
dx
dt
= y't
x't
,(15 )
Bu ifodani urinmaning (2.1.4) tenglamasiga qo‘yib, uni proporsiya shakliga
keltirish oson:
X − x
x '
t = Y − y
y '
t ( 16 )
Ko‘pincha ikkala maxrajni dt
ga ko‘paytirib, urinma tenglamasini
quyidagicha yoziladi:
X − x
dx = Y − y
dy . ( 17 )
Agar tanlangan nuqtada
y't=ψ't hosila noldan farqli bo‘lsa, x bilan y ning
rollarini almashtirib, urinmaning yana o‘sha tenglamasiga kelar edik. Bizning
muhokamalarimizni faqat ikkala hosila
x't va y't birdaniga nolga
aylangandagina qo‘llab bo‘lmaydi. Bunday nuqta egri chiziqning maxsus
nuqtasi deyiladi: unda urinmaning mavjud bo‘lmasligi ham mumkin. Bu
holda (16) yoki (17) tenglamalar o‘z ma’nosini yo‘qotadi: chunki ikkala
maxraj ham nolga aylanadi.
Misol tariqasida sikloidaga urinma o‘tkazish masalasini qaraylik:

x=a¿ . Bu holda:

x't=a(1− cos t),y't= asin t,
shu sababli, maxsus nuqtalar t = 2 πk ( k = 0 , ± 1 , ± 2 , … )
qiymatlarga javob
beruvchi nuqtalardan iborat. Maxsus nuqtalardan boshqa hamma nuqtalarda
(2.1.8) formula bo‘yicha:
tan α = sin t
1 − cos t = ctg t
2 = tan
( π
2 − t
2 ) ,
shuning uchun
α= π
2− t
2 deb qabul qilish mumkin.
Biz
t= ∡MDN ekanini esga olaylik , demak ∡ MEN = t
2 .
Agar
EM ni T
nuqtada x
o‘q bilan kesishguncha davom ettirsak, u holda
∡ ETx = π
2 − t = α .
26

Demak sikloidaning nuqtasi tegishli vaziyatda dumalovchi doiraning eng
yuqori nuqtasi bilan tutashtiruvchi ME to‘g‘ri chiziq urinmaning o‘zginasi
bo‘ladi. Bundan
MN to‘g‘ri chiziqning normal bo‘lishi ko‘rinadi.
Kelgusida normalning x
o‘q bilan kesishgan nuqtasigacha bo‘lgan n
kesmasi bizga kerak bo‘ladi, uni to‘g‘ri burchakli
MEN uchburchakdan topish
oson:
n = MN = 2 a sin t
2 .
Bu gal maxsus nuqtalarda urinmalar mavjud, ular
y o‘qqa paralleldir;
biroq egri chiziqning urinmaga nisbatan joylanishi odatdagicha emas; bu
nuqtalar o‘tkirlanish (qaytish) nuqtalaridir.

26

Xulosa.
Bizga ma’lumki funksiyaning differensiali matematik analiz asoslari
fanining muhim rivojlanayotgan tarmoqlaridaan biri bo‘lib hisoblanadi.
Ayniqsa differensialning geometriyaga tatbiqlari bo‘limi salohiyati va amaliy
qo‘llana bilishi jihatidan muhim ahamiyat kasb etadi va u juda ko‘p
tushunchalarni o‘z ichiga oladi. Funksiya ustida differensial amalini bajara
olish – matematik analiz asoslari fanini yaxshi o‘zlashtirish, unga tegishli
bo‘lgan tushunchalar va turli masalalarni yechishga, ularni oson hal qilishga
imkon beradi.
Bu kurs ishini tayyorlash davomida quyidagilarni o‘rganildi:
1. Funksiya monotonligi haqida tushuncha;
2. Funksiyaning ekstremum qiymatlarini uning hosilasi yordamida topish;
3. Funksiya qavariqligi va botiqligi;
4. Funksiyaning egillish nuqatalarini aniqlash;
5. Funksiyaning aasiimptotaalari;
6. Funksiyani tekshirish;
7. Egri chiziqlarning tekislikda analitik ifodalanishi;
8. Yassi egri chiziqqa urinma.
Ushbu kurs ishini tayyorlash davomida funksiya differensiali yordamida
funksiyaning monotonligini aniqlashga doir teoremalar va ularning
isbotlari, funksiya ekstremumini topishda uning yuqori tartibli
hosilalaridan foydalanish, ekstremumning zarur va yetarlilik shartlari,
funksiya qavariq va botiqlik tushunchalari, funksiyalarni tekshirish,
shuningdek differensial hisobning geometriyaga tatbiqlari bilan tanishildi.
26

Foydalanilgan adabiyotlar
1. Alimov SH.O. Ashurov R.R. Matematik analiz 1,2,3 q.T. “ Mumtoz
so’z” 2018.
2. G. Xudoyberganov, A. K. Vorisov, X. T. Mansurov, B. A. Shoimqulov.
Matematik analizdan ma’ruzalar 1-qism. T: “Voris-nashriyot” 2010 yil
3. B. A. Shoimqulov, T. T. Tuychiyev, D. H. Djumaboyev. Matematik
analizdan mustaqil ishlar. T: “O‘zbekiston faylasuflari milliy jamiyati”
2008 yil.
4. Sadullayev A., Mansurov X.T., Xudoyberganov G., Vorisov A.K.,
G’ulomov R. Matematik analiz kursidan misol va masalalar
to’plami,1,2,3 q. T.”O’qituvchi”, 1995,1995,2000.
5. Shokirova X.R Karrali va egri chiziqli integrallar.
T.”O’zbekiston”,1990.
6. Canuto C., Tabacco A. Mathematical Analysis, II. Springer-Verlag,
Italia, Milan, 2008.
7. Azlarov T.A., Mansurov X.T. Matematik analiz,1,2
q.T.”O’qituvchi”,1994,1995.
Internet saytlari.
1. http://www.ziyonet.uz/
2. http://www.allniath.ru/
3. http://www.mcce.ru/
4. http://www.mexmat.ru/
5. http://www.webmath.ru/
6. http://www.exponenta.ru/
7. www.lib-homelinex.org/math
8. www.eknigu.com/lib/Mathematics/
26

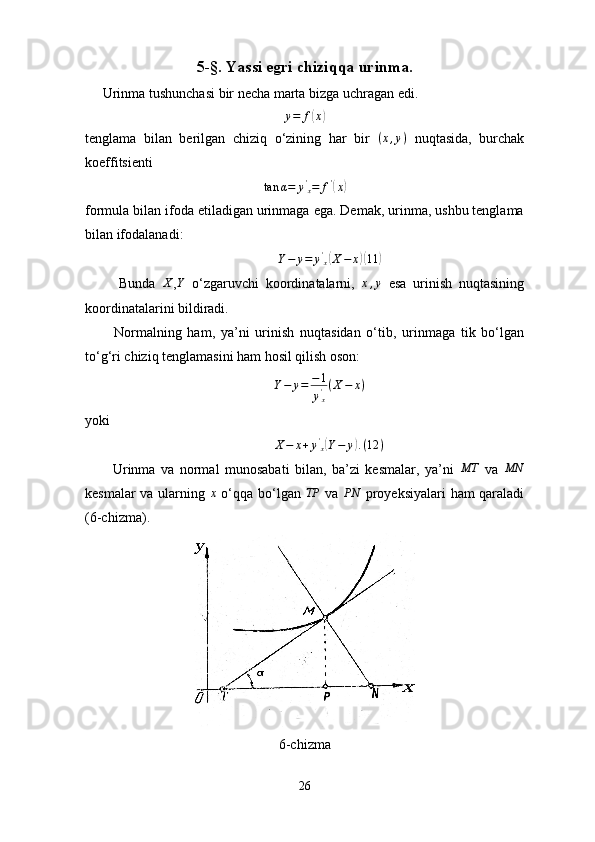
Differensial hisobning geometriyaga ba’zi bir tatbiqlari

Купить

Похожие документы
R m fazo va unda ketma-ketlik kurs ishi
Oshkormas funksiyalar va ularning hosilalari
Ko‘p o‘zgaruvchili funksiyaning xususiy hosilalari
Ikkinchi tur xosmas integrallar
Aniq integrallarning geometriyaga tatbiqlari