Дата регистрации 15 Апрель 2025
0 ПродажIkkilik daraxtlar va ular ustida amallar
















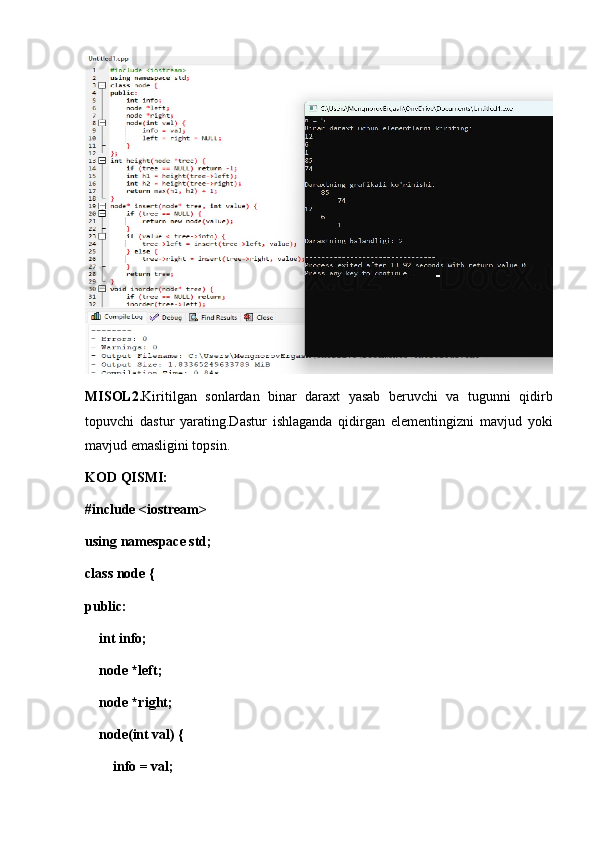


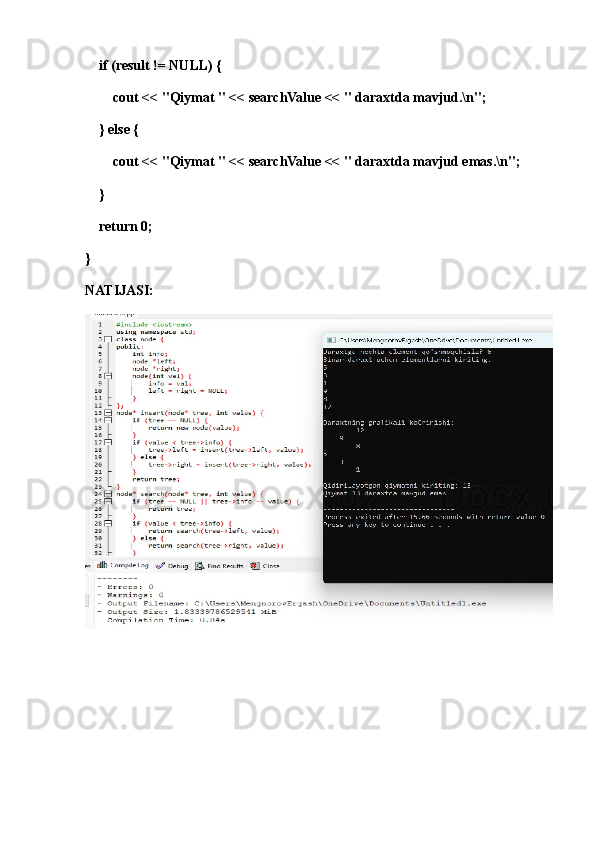
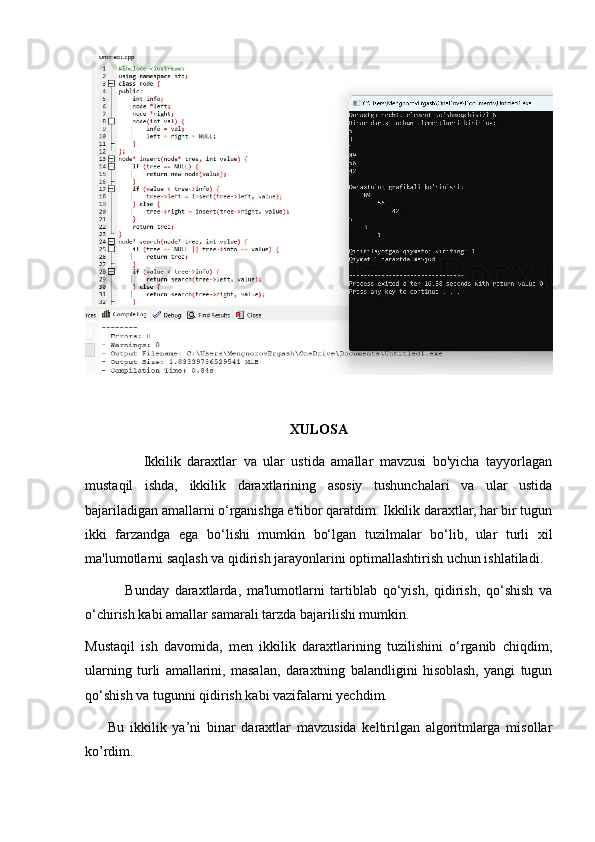

Ikkilik daraxtlar va ular ustida amallar
-
Похожие документы
- Avtobus yo‘nalishlari va chiptalar sotuvini boshqarish tizimi uchun ma’lumotlar bazasi
- Restorandagi stol bron qilish tizimi uchun ma’lumotlar bazasini yaratish
- Microsoft Publisher dasturi ishlatilishi
- Pythonda sanoq sistemalari va kompleks sonlar bilan ishlash
- Zamonaviy kompyuterlar va ulaming arxitekturasi. Xotira qurilmasi, axborotlami kiritish - chiqarish qurilmalari