Информация о документе

Цена 150000UZS
Размер 1.7MB
Покупки 0
Дата загрузки 13 Июнь 2025
Расширение docx
Раздел Диссертациии
Предмет Алгебра

Продавец

Urokov Orif

Дата регистрации 11 Январь 2024

21 Продаж

Buziluvchan va aralash turdagi tenglamalar.

Купить
MUNDARIJA KIRISH……………………………………….……………3 1-BOB . Buziluvchan va aralash turdagi tenglamalar. Gipergeometrik funksiya, kasr-tartibli integro-differensial operatorlar, elliptik tipdgi tenglamalar uchun ekstremum prinsipi 1.1-§. Aralash tipdagi tenglamalarning rivojlanishi 1.2-§. Gipergeometrik funksiya va uning xossalari 1.3-§. Kasr tartibli integro-differensial operatorlar 1.4- §. Xopf prinsipi va Zarembo-Jiro prinsipi haqida I bob bo’yicha xulosa 2-BOB.Chegaraviy xarakteristikaning bir qismida Trikomi va ichki xarakteristikada siljishli shart berilgan masala ( TI ) yechimining yagonaligi 2.1-§. TI masalaning qo’yilishi 2.2-§. va funksiyalar orasidagi birinchi va ikkinchi funksional munosabatlarni hosil qilish 2.3-§. TI masala yechimining yagonaligi II bob bo’yicha xulosa 3-BOB. TI masala yechimining mavjudligi 3.1-§. va funksiyalar orasidagi munosabatni keltirib chiqarish 3.2-§. Singulyar integral tenglamani regulyarizatsiyalash 3.3-§. Viner-Hopf integral tenglamasini hosil qilish III bob bo’yicha xulosa XULOSA…………………………………………………… FOYDALANILGAN ADABIYOTLAR …………… ……. KIRISH Magistrlik dissertatsiyasi mavzusining asoslanishi va uning dolzarbligi . Respublikamizda yoshlarning bilim olishi, mamlakatimizning rivojlanishiga ularni keng jalb qilish bo yicha 2017-yil 20-apreldagi “Oliy ta limʻ ʼ tizimini yanada rivojlantirish chora-tadbirlari to g risidagi” PQ-2909 qarori asosida ʻ ʻ olib borilayotgan ishlar va tadbirlarda, shuningdek rejalashtirilayotgan vazifalarda oliy ta lim muassasalari ilmiy salohiyatini mustahkamlash, oliy ta limda ilm-fanni ʼ ʼ yanada rivojlantirish, uning akademik institutlar bilan integratsiyalashuvini kuchaytirish, iqtidorli talaba yoshlarni ilmiy faoliyat bilan shug ullanishga keng ʻ jalb qilish orqali ularning bilim darajasini yanada mustahkamlash masalalariga katta e tibor berilgan. “Bizning vazifamiz-to plangan tajriba va ilg or xalqaro ʼ ʻ ʻ amaliyotga suyangan holda, o zimizning taraqqiyot va yangilanish modelimizni ʻ qat iy amalga oshirishdan iborat” [1] . Respublikamizda “Ta lim to g risida” gi ʼ ʼ ʻ ʻ Qonun va “Kadrlar tayyorlash milliy dasturi” ning amalga oshirilayotganligi munosabati bilan umumiy o rta va o rta maxsus, kasb-hunar ta limi va Oliy ta lim ʻ ʻ ʼ ʼ muassasalaridagi matematika ta limi mazmunining yangilanishi, ularning yangi ʼ jihozlari bilan ta minlanishi, ta lim jarayonida axborot texnologiyalaridan keng ʼ ʼ foydalanish bo lajak matematik o qituvchilarini tayyorlash mazmuniga bevosita ʻ ʻ ta sir ko rsatmoqda. Ularning bilim, ko nikma va malakalariga bo lgan talablar ʼ ʻ ʻ ʻ kuchaymoqda. O zbekiston Respublikasi Prezidenti Sh. M. Mirziyoyevning Oliy Majlisiga ʻ 2018-yilgi Murojaatnomasida “Yuqori malakali pedagog kadrlar tayyorlash va qayta tayyorlashga e tibor berish lozim. Kadrlar tayyorlashning sifati, erkin ʼ fikrlovchi shaxsni kamol toptirish, ertaga sinfxonalar va auditoriyalarda kimlar dars va saboq berishiga bog liq. Yana bir bor ta kidlab o tishga to g ri keladi: ʻ ʼ ʻ ʻ ʻ amalga oshirilayotgan barcha islohotlarning taqdiri shu masalaga, ya ni kadrlar ʼ tayyorlashga chambarchas bog liqligini biz aniq va ravshan anglab olishimiz ʻ lozim. O zini shu mamlakatning haqiqiy vatanparvari deb biladigan har bir kishi ʻ bu dasturni amalga oshirishga o z mehnatini, o z ulushini qo shadi, debʻ ʻ ʻ ishonaman” deya ta kidlab o tgan edi [2]. ʼ ʻ Ma lumki, ko p bosqichli ta lim tizimida o rta umumta lim, o rta maxsus, ʼ ʻ ʼ ʻ ʼ ʻ kasb-hunar ta limi (akademik litsey va kasb-hunar kollejlari), Oliy ta lim ʼ ʼ (bakalavriat va magistratura) da matematika kursi o rganiladi. Xususan, ʻ matematika kursida dars mashg ulotlarining mazmuni va uni tashkil etish ʻ uslublarini takomillashtirish o qitish metodikasida dolzarb vazifalardan biri ʻ hisoblanadi. Talaba va magistrlarning yuqori saviyadagi bilim va mahoratga ega bo lishida matematik praktikum va nazariyaning o rni juda muhimdir. Praktikum ʻ ʻ paytida talaba va magistrlar o z bilimlarini oshirib, olgan nazariy bilimlarini ʻ mustahkamlab, matematikaning asosiy tushunchalari va qonuniyatlarini chuqurroq anglab, eksperimental masalalarni yechish ko nikma va malakalarini egallab, ʻ o rganib tajribalarini mustaqil bajarish natijalarini matematik qayta ishlash ʻ usullarini o zlashtirib oladilar. ʻ Keyingi vaqtlarda respublikamizda va dunyo miqyosida olib borilayotgan ilmiy tadqiqotlar singulyar koeffitsiyentli aralash tipdagi tenglamalar uchun lokal va nolokal chegaraviy masalalarni tadqiq etish muhim ekanligini ko’rsatmoqda. Buziluvchan giperbolik, elliptik va aralash turdagi tenglamalar uchun chegaraviy masalalar nazariyasi zamonaviy xususiy hosilali differensial tenglamalar nazariyasining asosiy yo’nalishlaridan biri hisoblanadi va muhim amaliy masalalarni yechishda qo’llaniladi. Hozirgi kunda jahon miqyosida singulyar koeffitsiyentli aralash turdagi tenglamalar (SKATT) va soha ichida buziladigan singulyar koeffitsiyentli giperbolik turdagi tenglamalar (SIBSKGTT) uchun chekli va chegaralanmagan sohalarda nolakal shartli chegaraviy masalalarni tadqiq etish bo’yicha muhim qadamlar qo’yilmoqda. Ayniqsa, ta’riflangan masalalarda lokal va nolokal shartlarni nostandart qo’yilishi, jumladan: Frankl shartiga o’xshash shartni ichki xarakteristikada berilishi [5], siljishli shartni ichki ichki xarakteristikada berilishi [12] , Bitsadze-Samarskiy shartini chegaraviy va unga parallel ichki xarakteristikada berilishi tadqiqotlarda katta qiziqish uyg’otmoqda . Bunday masalalar tadqiqoti shu vaqtgacha o’rganilmagan yangi turdagi Trikomining nostandart singulyar integral tenglamalarni tadqiq etishga olib kelmoqda . Bu yerda yadroning nosingulyar qismi nokarlamen tipidagi siljishga ega hamda tenglamaning noxarakteristik qismida nofredgolm operatori ishtirok etadi. Buziluvchan, elliptik va aralash turdagi tenglamalar nazariyasining rivojlanishi dastlab G. Darbu [3], F.Trikomi [3], E. Xolmgren [3] va S. Gellerstedtlarning [4] mos ravishda 1894, 1923, 1927 va 1938- yillarda e’lon qilingan fundamental ishlaridan boshlangan. Aralash turdagi tenglama uchun birinchi fundamental tadqiqotlar italiyalik matematik F.Trikomi tomonidan bajarilgan. Bu ishlardan keyin buziluvchan va aralash turagi tenglamalar uchun chegaraviy masalalar nazariyasi ko’p yo’nalishlarda o’rganildi va rivojlantirildi, jadallik bilan rivojlanib ketdi, bu yo’nalishda salmoqli ilmiy natijalar quyidagi ishlarda olindi: A.V.Bitsadze [4] , M.M.Smirnov[5] , M.S. Salohitdinov [6], T.D.Djurayev [7], A.M.Naxushev [8], E.I.Moiseyev [9], A.P.Soldatov [10] , A.I. Kojanov [11] monografiyalarida keltirilgan. Hozirgi kunda jahon miqyosida singulyar koeffitsiyentli aralash turdagi tenglamalar (SKATT) va soha ichida buziladigan singulyar koeffitsiyentli giperbolik turdagi tenglamalar (SIBSKGTT) uchun chekli va chegaralanmagan sohalarda nolakal shartli chegaraviy masalalarni tadqiq etish muhim ahamiyat kasb etmoqda. Ayniqsa, ta’riflangan masalalarda lokal va nolokal shartlarni nostandart qo’yilishi, jumladan: Frankl shartiga o’xshash shartni ichki xarakteristikada berilishi, siljishli shartni ichki ichki xarakteristikada berilishi, Bitsadze-Samarskiy shartini chegaraviy va unga parallel ichki xarakteristikada berilishi tadqiqotlarda katta qiziqish uyg’otmoqda . Bunday masalalar tadqiqoti shu vaqtgacha o’rganilmagan yangi turdagi Trikomining nostandart singulyar integral tenglamalarni tadqiq etishga olib kelmoqda . Bu yerda yadroning nosingulyar qismi nokarlamen tipidagi siljishga ega., hamda tenglamaning noxarakteristik qismida nofredgolm operatori ishtirok etadi. Tadqiqot obyekti va predmeti . Singulyar koeffitsiyentli Gellerstedt tenglamasi va bu tenglama uchun buzilish chizig’ida Frankl shartlili masala. Tadqiqot ishning maqsadi va vazifalari . Dissertatsiyamizda tanlangan ishning maqsadi singulyar koeffitsiyentli aralash turdagi tenglamalar uchun tenglama tipi o’zgarish chizig’ida Frankel shartlili masalalarni o’rganish. Ilmiy yangiligi . Dissertatsiya ishining ilmiy yangiligi shundan iboratki, singulyar koeffitsiyentli aralash tipdagi tenglama uchun ichki xarakteristikada 2 siljishli masala o’rganilgan. Tadqiqotning asosiy masalalari va farazlari . Ushbu ishda birlamchi masalalar sifatida quyidagilarni ko’rib o’tish belgilangan: • Masalani qo’yish • Masala yechimining yagonalini isbotlash • Yechimning majudligini isbotlash Mavzu bo’yicha adabiyotlar tahlili . Magistrlik dissertatsiyasi mavzusiga yaqin masalalarni yechish usullari М ирсабурова . Г . М . Комбинированние задачи с локалними и нелокалними краевими условиями для уравнения Геллерстедтас сингулярним коиффициентом - М. : Наука . 2024.79 c., . Mirsaburov M. Singulyar koeffitsiyentli Gellerstedt tenglamasi uchun Trikomi masalasi. Termiz -“ Surxon - nashr ” 224 b ., Салахитдинов М.С. , Мирсабуров М. Нелокальние задачи для уравнений смешанного типа с сингулярними коеффициентами. Тошкент. Nomli ilmiy adabiyotlardan topish mumkin. Bu manbalarda umumlashgan Trikomi tenglamasi uchun Gellerstedt shartli masala atroflicha bayon qilingan. Tadqiqotda qo’llanilgan metodikaning tavsifi . Tadqiqot ishimizda differensial va integral tenglamalarni yechish usullaridan, Xopf-prinsipi, Zarembo-Jiro prinsipi, inetegral tenglamani regulyarizatsiyalash usullaridan foydalanildi. Tadqiqot natijalarining nazariy va amaliy ahamiyati. Ushbu magistrlik dissertatsiyasi nazariy ahamiyatga ega. Dissertatsiyada olingan natijalardan kelgusida singulyar koeffitsiyentli aralash tipdagi tenglamalarni yechishda va matematika yo’nalishida talabalarga maxsus fanlardan dars berishda foydalanish mumkin. Ishning tuzilishi va mazmuni . 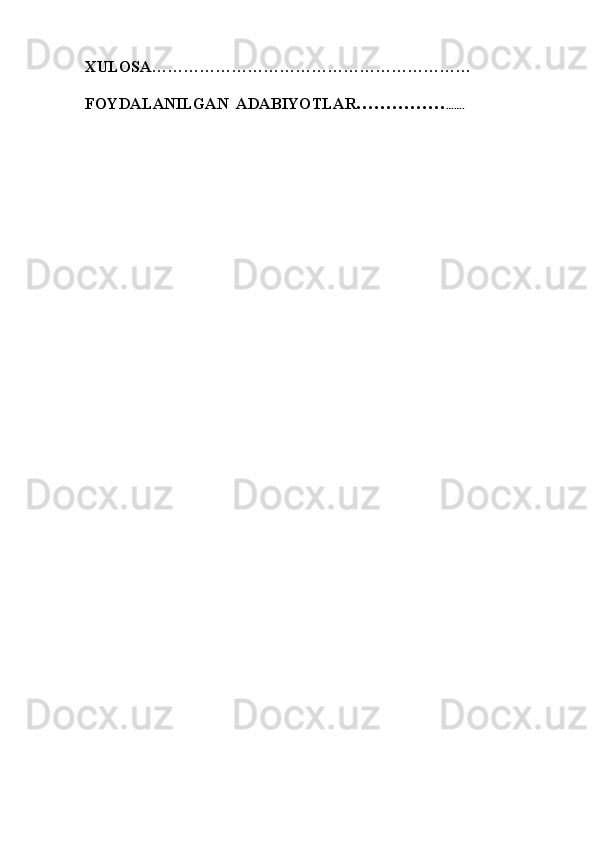Magistrlik dissertatsiyasi kirish, uchta bob, xulosa, foydalanilgan adabiyotlar ro’yxatidan iborat. Quyida bajarilgan ishlar haqida qisqacha ma’lumotlar keltirilgan: Uning kirish qismida tadqiqot mavzusining dolzarbligi va uning o’rganilganlik darajasi batafsil bayon qilinib, tadqiqotning maqsad va vazifalari ko’rsatib o’tilgan. Dissertatsiyaning birinchi bobi 3 ta paragrafdan iborat bo’lib, kelgusida tadqiqot uchun kerak bo’ladigan nazariy ma’lumotlar keltirilgan, Dissertatsiyaning ikkinchi bobi ham 3 ta paragrafdan iborat bo’lib TI masalaning qo’yilishi va yagonaligiga bag’ishlangan. Uchinchi bobda esa TI masala yechimi mavjudli isbotlangan. Dissertatsiyaning har bir bob oxirida bob bo’yich xulosalar keltirilgan bo’lib, oxirida umumiy xulosa va foydalanilgan adabiyotlar ro’yxati keltirilgan. I BOB Buziluvchan va aralash turdagi tenglamalar. Gipergeometrik funksiya, kasr-tartibli integro-differensial operatorlar, elliptik tipdgi tenglamalar uchun ekstremum prinsipi 1.1- §. Aralash tipdagi tenglamalarning rivojlanish i Xususiy hosilali differensial tenglamalar uchun kombinatsiyalashgan lokal va nolokal shartli masalalar dastlab Chapligin tenglamasi (aralash turdagi tenglama) F.I.Frankl (1956) tomonidan ta’riflangan va Yu.V.Devingtal (1959) tomonidan masala y е chimining yagonaligi va mavjudligi isbotlangan. Li Szin-bin (1961) esa Frankl masalasi y е chimining yagonaligini abc usuli yordamida ko’rsatgan. A.V.Bitsadze va A.A.Samarskiylarning hammualliflik maqolasida (1969) Laplas tenglamasi uchun yangi tipdagi kombinatsiyalashgan lokal va nolokal s hartli masalaning korrektligi isbotlangan. A.M.Naxushev Trikomi tenglamasi uchun siljishli masalani (1969) ta’rifladi va bu masala y е chimining yagonaligi va mavjudligini isbotladi. Bu ishlardan so’ng singulyar koeffitsiyentli Gellerstedt tenglamasi uchun kombinatsiyalashgan lokal va nolokal shartli masalalarning turli modefikatsiyalari M.Mirsaburov va uning shogirdlari tomonidan ta’riflandi va noklassik masalalar nostandart singulyar integral tenglamalarga olib kelinib o’rganildi. Frankl masalasining qo’yilishi Ushbu Chapligin tenglamasini o’rganamiz (1.1.1) bu y е rda - uzluksiz differensiallanuvchi funksiya bo’lib, agar bo’lsa. agar bo’lsa, va shu bilan birga . -chekli bir bog’lamli soha bo’lib u o’qining (bu y е rda , ) kesmasi bilan, uchlari va nuqtalarda bo’lgan va yuqori yarim tekislikda yotuvchi silliq Jordan chizig’i bilan, o’qining ( bu y е rda ) kesmasi bilan va (1.1.1) tenglamaning xarakteristikasi bilan chegaralangan. Frankl masalasi [9]: sohada (1.1.1) tenglamaning ushbu shartlarni qanoatlantiruvchi regulyar y е chimi topilsin. , , , , , , , , (1.1.2) bu y е rda va funksiyalar Gyolder shartini qanoatlantiruvchi berilgan funksiyalar, , funksiya ham berilgan funksiya bo’lib, uning birinchi tartibli hosilasi intervalda Gyolder shartini qanoatlantiradi. Bu masalaning yangiligi shundan iboratki, aralash sohaning (elliptik) va (giperbolik) qismlarida chegaraviy shartlar nolokal (1.1.2) usulda beriladi. Bitsadze-Samarskiy masalasining qo’yilishi Ushbu Laplas tenglamasini o’rganamiz. (1.1.3) soha tekisligining ushbu to’g’ri chiziq kesmalari bilan chegaralangan bir bog’lamli sohasi bo’lsin: ; ; ; ; Bitsadze-Samarskiy masalasi[10]: sohada (1.1.3) tenglamaning ushbu shartlarni qanoatlantiruvchi regulyar y е chimi (garmonik funksiya) topilsin. , , , . , , , , (1.1.4) bu y е rda - berilgan uzluksiz funksiyalar. Bu masalaning yangiligi shundan iboratki, berilgan masala y е chimining chegaraviy qiymatlari soha ichida takrorlanadi. (Sohaning ichki nuqtalarida (1.1.4) tenglikni qanoatlantiradi), ya’ni chegaraviy shart (1.1.4) nolokal usulda beriladi. Siljishli masalaning qo’yilishi Ushbu Gellerstedt tenglamasini[3] o’rganamiz , (1.1.5) soha tekisligining bir bog’lamli sohasi bo’lib, u yuqori yarim tekislik da yotuvchi uchlari va nuqtalarda bo’lgan Jordan chizig’i bilan va quyi yarim tekislik da (1.1.5) tenglamaning va xarakteristikalari bilan chegaralangan bo’lsin. Siljishli masala[11]. sohada ushbu shartlarni qanoatlantiruvchi topilsin. 1 0 ) sohada (1.1.5) tenglamaning regulyar y е chimi; 2 0 ) sohada (1.1.5) tenglamaning sinfga tegishli umumlashgan y е chimi; 3 0 ) funksiya ushbu shartlarni qanoatlantiradi. , , bu y е rda va lar (1.1.5)tenglamaning , nuqtalardan chiquvchi xarakteristikalarning mos ravishda va xarakteristikalar bilan kesishish nuqtalarining affikslaridir, , , , - berilgan uzluksiz funksiyalar. Shu bilan birga , , . Siljishli masalasining o’ziga xos yangiligi shundan iboratki, bu y е rda ikkala va chegaraviy xarakteristikalarda chegaraviy shart berilgan. Trikomi masalasida faqat bir chegaraviy xarakteristikada beriladi, ikkinchi chegaraviy xarakteristika esa chegaraviy shartdan ozod qilinadi. Yuqorida ta’riflangan uchchala: Frankl, Bitsadze-Samarskiy, siljishli masalalarda o’ziga xos umumiylik shundan iboratki, chegaraviy shartlarda lokal va nolokal shartlar ishtirok etmoqda 1.2- §. Gipergeometrik funksiya va uning xossalari Buziladigan giperbolik va elliptik tipdagi tenglamalar nazariyasida ushbu (1.2.1) Gauss tenglamasining yechimlari fundamental ahamiyatga ega, bu yerda - parametrlar bo’lib, ular ixtiyoriy kompleks yoki haqiqiy sonlar bo’lishi mumkin. Gauss tenglamasi uchta: 0,1, regulyar maxsus nuqtalarga ega. O’zgaruvchilarni maxsus almashtirish yordamida buziluvchan giperbolik va elliptik tipdagi tenglamalar (1.2.1) tenglamaga olib kelinishi mumkin va bu tenglamaning yechimlaridan mos ravishda Riman funksiyasini, Grin funksiyasini tuzishda fundamental ahamiyatga ega. Dastlab (1.2.1) tenglamaning yechimini nuqta atrofida topamiz. Yechimni (1.2.2) darajali qator ko’rinishida izlaymiz. Bu yerda - hozircha noma’lum sonlar. (1.2.2) dan ushbu hosilalarni hisoblaymiz: , . Endi bu hosilalarni (1.2.1) tenglamaga qo’yib, quyidagi munosabatni hosil qilamiz: , bu yerdan oldidagi umumiy koeffitsiyentni nolga tenglashtirib, ushbu , rekkurent formulaga kelamiz. Gauss tenglamasining bir jinsli ekanligidan foydalanib, umumiylikni buzmasdan deb qabul qilamiz va , (1.2.3) Gaussning gipergeometrik qatoriga kelamiz, bu yerda , belgilashlar kiritilgan. Gipergeometrik funksiyaning sodda xossalarini keltiramiz, bu xossalar (1.2.3) darajali qatorning ko’rinishidan bevosita kelib chiqadi. 1.Agar yoki bo’lsa, (bu yerda n=0,1,2,… ) (1.3) darajali qator uziladi, ya’ni yoki -darajali ko’phadga aylanadi; 2. gipergeometrik funksiya va parametrlarga nisbatan simmetrikdir, ya’ni (1.2.4) 3. bo’lganda (1.2.5) tenglikka ega bo’lamiz. (1.2.1) tenglamaning ikkinchi yechimini topish uchun o’rniga (1.2.6) formula yordamida yangi funksiya kiritamiz, bu yerda -hozircha ixtiyoriy noma’lum son. (1.2.6) tenglikni (1.2.1) tenglamaga qo’yib, ushbu tenglamaga ega bo’lamiz: Bu tenglamada deb olsak, u Gauss tenglamasiga aylanadi. Uni yechib Gauss tenglamasining ikkinchi yechimini topamiz: bu yerda (1.2.1) tenglamaning yechimini maxsus nuqta atrofida hosil qilish uchun ni ga almashtirish yetarlidir. Bu holda (1.2.1) tenglama parametrlari , , lardan iborat bo’lgan gipergeometrik tenglamaga aylanadi. Bu holda (1.2.1) tenglamaning nuqta atrofida , chiziqli erkli yechimlarni hosil qilish qiyin emas, bu yerda butun sonlar bo’lmasligi kerak. (1.2.1) tenglamaning yechimlarini cheksiz uzoqlashgan maxsus nuqta atrofida topish uchun erkli o’zgaruvchi va funksiyani ushbu formulalar yordamida almashtiramiz: , bu holda (1.2.1) tenglama funksiyaga nisbatan parametrlari bo’lgan gipergeometrik funksiyag aylanadi. Shunday qilib, (1.2.1) tenglamaning maxsus nuqta atrofidagi chiziqli erkli yechimlari ushbu ko’rinishda bo’ladi: , , bu yerda butun sonlar bo’lmasligi kerak. 1.3- §. Kasr tartibli integro-differensial operatorlar Ta’rif. , bo’lsin. Ushbu , , , , ko’rinishdagi ifodalar funksiyaning (kasr) tartibli (Riman-Luivill ma’nosidagi) integrallari deyiladi [3,4,6]. va funksiyalar oraliqning deyarli barcha nuqtalarida aniqlangan bo’lib, sinfga tegishli bo’ladi. Agar , bo’lsa, deyarli hamma uchun tenglik o’rinli bo’ladi. Ta’rif. funksiya kesmada aniqlangan bo’lsin. , , , , (1.3.1) ko’rinishdagi ifodalar funksiyaning (kasr) tartibli (Luivill ma’nosidagi) hosilalari deyiladi [3,4,6]. Kasr tartibli integrallar ixtiyoriy tartibgacha aniqlangan bo’lsa, (1.3.1) kasr tartibli hosilalar faqatgina bo’lganda aniqlangan. bo’lganda , , , . Odatda kasr tartibli integrallar ko’rinishida ifodalanuvchi funksiyalar sinfini bilan belgilanadi, ya’ni . Quyidagi teorema o’rinli. Teorema . bo’lsin. U holda , tengliklar barcha funksiyalar uchun, , (1.3.2) tengliklar esa mos ravishda barcha , funksiyalar uchun bajariladi. Agar oxirgi shartlar o’rniga bo’lsa, (1.3.2) tengliklar umuman olganda noto’g’ri bo’ladi va masalan, birinchisi quyidagi formula bilan almashadi: , bu yerda , . Endi ixtiyoriy kasr va butun tartibli integral va hosilalar yordamida quyidagi integro-differensial operatorlarni kiritamiz: (1.3.3) bu yerda . Operatorlar quyidagi xossalarga ega: 1.Agar , va bo’lsa, u holda deyarli barcha uchun munosabat o’rinli bo’ladi. 2.Agar va bo’lsa, u holda deyarli barcha uchun , munosabat o’rinli bo’ladi. 3. va bo’lsa, u holda deyarli barcha uchun , ayniyat o’rinli. 4. Agar bo’lsa, u holda ushbu , , , ayniyatlar o’rinlidir . 5. bo’lsin, u holda ushbu ayniyatlar o’rinlidir: , (1.3.4) (1.3.5). 1.4- §. Hopf prinsipi va Zarembo-Jiro prinsipi haqida Chegarasi bo’lgan sohada ushbu tenglamani tekshiramiz . sohada forma musbat aniqlangan. Hopf prinsipi [4]. Agar funksiya ushbu (1.4.1) tenglamaning aynan nolga teng bo’lmagan sohada regulyar , da uzluksiz yechimi bo’lib, shart bajarilsa, u holda barcha sohada , agarda bo’lsa, tengsizlik o’rinli bo’ladi. Zarembo-Jiro prinsipi [4]. funksiya elliptik tipga tegishli bo’lgan (1.4.1) tenglamaning sohadagi regulyar yechimi bo’lsin. Agar soha chegarasining nuqtasida o’zining ekstremal qiymatini qabul qilib, kontur shunday xossaga ega bo’lsaki, da yotuvchi nuqtadan aylanacha o’tkazish mumkin bo’lsa, u holda aylanachaning markaziga qarab yo’nalgan radius bo’yicha olingan hosila ( agar u mavjud bo’lsa) nuqtada noldan farqli bo’ladi; shu bilan birga maksimum bo’lgan holda , minimum bo’lgan holda esa bo’ladi. I bob bo’yicha xulosa Dissertatsiyaning ushbu 1-bobi to’rtta paragrafdan iborat bo’lib, u aralash tipdagi tenglamalarning rivojlanish tarixi, Gaussnig gipergeometrik funksiyalari, integro-differensial operatorlar va ularning xossalari, elliptik tipdagi tenglamalar tenglamalar uchun ekstremum prinsipi kabi nazariyalarga bag’ishlangan. Gipergeometrik funksiyaning integral ifodasi keltirib chiqarilgan. Kasr tartibli integrallar, kasr tartibli hosilalar, integro-differensial operatorlarning xossalari bayon qilingan. Elliptik tipdagi tenglamalar nazariyasida muhim o’rin tutuvchi Hopf prinsipi va Zarembo-Jiro prinsipi keltirib o’tilgan. II BOB. Chegaraviy xarakteristikaning bir qismida Trikomi va ichki xarakteristikada siljishli shart berilgan masala ( TI ) yechimining yagonaligi 2.1-§. TI masa laning qo’yilishi Ushbu tenglamani o’rganamiz , (2.1.1) bu yerda va o’zgarmas sonlar bo’lib, ular uchun , tengsizlik o’rinli. soha kompleks tekislikning chekli bir bog’lamli sohasi bo’lib, u yarim tekisligida joylashgan va uchlari va nuqtalarda bo’lgan, (2.1.1) tenglamaning normal chizig’i bilan , yarim tekislikda esa tenglamaning va xarakteristikalari bilan chegaralangan bo’lsin. Ushbu belgilashlarni kiritamiz: va lar orqali sohaning mos holda va yarim tekisliklarda yotuvchi qismlarini , va nuqtalar orqali esa nuqtadan chiquvchi xarakteristikalarning mos ravishda va xarakteristikalar bilan kesishish nuqtalarini belgilaymiz. Xuddi shunday va nuqtalar orqali esa nuqtadan chiquvchi xarakteristikalarning mos ravishda va xarakteristikalar bilan kesishish nuqtalarini belgilaymiz. Bu yerda - o’qining intervali, , . ( bunda , ) akslantirish nuqtalar to’plamini nuqtalar to’plamiga akslantiruvchi chiziqli funksiya va , bo’lsin. ( bunda , ) –akslantirish esa nuqtalar to’plamini nuqtalar to’plamiga akslantiruvchi chiziqli funksiya va , bo’lsin. MASALA. sohada quyidagi shartlarni qanoatlantiruvchi funksiya topilsin. 1. ( funksiya sohada uzluksiz). 2. va bu sohada (2.1.1) tenglamani qanoatlantiradi. 3. funksiya sohada sinfga tegishli bo’lgan umumlashgan yechim. 4. Intervalda ushbu ulanish sharti bajariladi : (2.1.2) va bu limitlar , , nuqtalarda dan kichik tartibda maxsuslikka ega bo’lishi mumkin, bunda . 5. , , (2.1.3) 6. , , (2.1.4) 7. , , (2.1.5) 8. , , (2.1.6) bunda , , - o’zgarmas sonlar , , ; , , , lar – mos ravishda va nuqtalardan chiquvchi xarakteristikalarning va xarakteristikalar bilan kesishish nuqtalarining affikslari bolib, , , . , , , -berilgan funksiyalar , bunda , . 2.2-§. va funksiyalar orasidagi funksional munosabatlarni hosil qilish Shakli o’zgargan Koshi masalasining yechimini beruvchi Darbu formulasi (2.1.1) tenglama uchun quyidagi ko’rinishda bo’ladi: , (2.2.1) bu yerda , , va larning qiymatlarini Darbu formulasidan hisoblaymiz. , bunda . Endi kabi almashtirish bajaramiz : , , , , , , . . Oxirgi tenglikda integral chegarasini o’zgartirish uchun quyidagi almashtirishni bajaramiz: , , , , . . Yuqoridagi tenglikda almashtirish bajaramiz: , , , , , , . . Oxirgi tenglikda ham integral chegrasini o’zgartiramiz: , , , , Endi va larning qiymatlarini (2.1.5) tenglikka olib borib qo’yamiz: . Yuqoridagi tenglikka operatorni qo’llaymiz : . . Oxirgi tenglikning chap va o’ng qismini ga bo’lamiz : (2.1.6) shartni e’tiborga olsak, yuqoridagi tenglik quyidagi ko’rinishni oladi: . Oxirgi tenglikni ushbu , (2.2.2) ko’rinishda yozib olamiz, bunda . (2.2.2) tenglik va lar o’rtasidagi 1-funksional munosabatdir. Endi va noma’lum funksiyalar orasidagi 2-funksional munosabatni keltirib chiqaramiz: Darbu formulasidan foydalanib, ni hisoblaymiz : xarakteristikada , , . Buni e’tiborga olsak, , bu yerda . Yuqoridagi tenglikda integral o’zgaruvchisini almashtirish uchun quyidagicha almashtirish bajaramiz: , , , , ; , . U holda , . , . Oxirgi tenglikda ni ga almashtirib, intervalni intervalga akslantiramiz: , . . Yuqoridagi tenglikka operatorni qo’llaymiz: Ya’ni , , (2.2.3) bunda, . Yuqoridagi tenglik va lar o’rtasidagi 2-funksional munosabatdir. 2.3-§. TI masala yechimining yagonaligi Faraz qilaylik, masala 2 ta va yechimga ega bo’lsin . U holda, funksiya ham masala yechimi bo’ladi. 1-teorema. ( A.V.Bitsadzening ekstremum prinsipi) sohada masalaning yechimi , , , , , , shartlar bajarilganda o’zining eng katta musbat (EKMus) va eng katta manfiy (EKMan) qiymatini yopiq sohaning normal chizig’i nuqtalarida qabul qiladi. Isbot. Bizga ma’lumki, Xopf prinsipiga ko’ra funksiya o’zining eng kata manfiy va emg kichik musbat qiymatini soha ichida qabul qilmaydi. Faraz qilaylik, funksiya o’zining eng katta musbat qiymatiga sohaning o’qida yotuvchi intervalidagi nuqtada erishsin. nuqta funksiyaning (EKMus) nuqtasi bo’lsin, bunda . U holda . Keling, 4 ta mumkin bo’lgan holatni alohida holni ko’rib chiqaylik : , , , va . 1.Aytaylik, bo’lsin. U holda bu nuqta (EKMus) nuqta bo’lganligi uchun Zarembo-Jiro prinsipiga ko’ra . Ma’lumki, funksiyaning (EKMus) nuqtasida kasr tartibli differensial operatorlar uchun quyidagi tengsizliklar o’rinli bo’ladi : , , bunda . Demak, (2.2.3) munosabat tufayli ( bunda bo’lganli uchun ) bo’ladi. Ulanish sharti (2.1.2) tufayli yuqoridagi ikki tengsizlik bir-biriga ziddir. Shuning uchun . 2. bo’lsin . Faraz qilaylik, nuqta tenglamaning yechimi. Ya’ni . U holda bunga mos keluvchi bir jinsli shartdan ni olamiz . nuqta uchun quyidagilar o’rinli , , . Bundan esa tenglikni nuqta uchun yozib, o ‘zaro zid tengsizliklarga kelamiz. Shuning uchun . 3. bo’lsin. Faraz qilaylik, nuqta tenglamaning yechimi bo’lsin: . U holda bo’ladi. , , larni e’tiborga olsak, yana quyidagi zid tengsizliklarga kelamiz . Bunda bo’lganda dir. Demak, . 4. bo’lsin.(2.1.5) shartda deb olsak va ni e’tiborga olsak, , , kelib chiqadi. bo’lganligi uchun . Lekin boshqa tomondan nuqta EKMus nuqta bo’ganligi uchun bo’lishi kerak. Zidlikka keldik. Demak, . bo’lsin. U holda (2.1.6) shartdan uchun , unga mos bir jinsli shartni e’tiborga olsak , ni olamiz, bunda . ekan. Ammo nuqtani EKMus nuqta deb olganligimiz uchun bo’lishi kerak. Zidlikka keldik, shuning uchun . Demak, 1-teorema shartlarini qanoatlantiruvchi kerakli funksiya sohadagi o’zining eng katta musbat qiymatiga sohaning normal chizig’ida erishar ekan. 1-toerema shartlarini qanoatlantiruvchi kerakli funksiya sohadagi eng kichik manfiy qiymatiga normal chiziqda erishishini ham xuddi yuqoridagi kabi ko’rsatish mumkin. 1-teorema isbotlandi . Natija. 1-teorema dagi shartlar bajarilganda, TI masala bittadan ortiq yechimga ega emas. Isbot. Bir jinsli chegaraviy shartlar ( , , , ) uchun aralash sohada masala yechimi ekanligini ko’rsatamiz. Haqiqatan ham, unga mos keluvchi bir jinsli shart tufayli, (2.1.3) shartdan ni olamiz. funksiya chiziqda nolga teng. Lekin biz yuqorida bu funksiya sohadagi o’zining eng katta musbat va eng kichik manfiy qiymatlariga chiziqda erishishini isbotladik. Ammo bizga ma’lumki, funksiya sohada uzluksiz bo’lganligi uchun, Veyershtrass teoremasiga ko’ra bu funksiya bu sohada eng katta musbat va eng kichik manfiy qiymatlarga erishishi kerak. Demak, sohada ekan. U holda , ; , , shuning uchun funksiyaning aralash sohada uzluksizligi va (2.1.2) ulanish sharti tufayli , ; , . (2.3.1) Endi sohada masala yechimi Darbu formulasi yordamida tiklanadi va (2.3.1) shartni e’tiborga olsak, shakli o’zgargan Koshi masalasining yechimi nolga teng. Ya’ni sohada . Shunday qilib , butun sohada ekan. III BOB. TI masala yechimining mavjudligi 3.1-§. va funksiyalar orasidagi funksional munosabatni keltirib chiqarish , , (3.1.1) bunda , . , . (3.1.1) tenglikni va lar uchun yozamiz: , . U holda, (2.2.2) tenglikka ko’ra . Oxirgi tenglikni har ikkala tomonini ga bo’lamiz : , bunda , . , . . Endi yuqoridagi tenglikdagi ba’zi integrallarning chegarasini o’zgartiramiz : 1. bo’lsin : , , , . U holda shu almashtirishdan foydalangan holda quyidagi integrallarni chegaralarini o’zgartiramiz : 1) . 2) . 3) . 4) . 2. bo’lsin : , , , . Yuqoridagi almshtirishdan foydalanamiz: 1) . 2) . 3) . 4) . Yuqoridagi almshtirishlardan so’ng (11) tenglik quyidagi ko’rinishga keladi : . Oxirgi tenglikni har ikkala tomonini ga ko’paytiramiz : . , (3.1.2) Bu yerda , , , , , , , , , , , , . Endi yuqoridagi 12 ta integralni hisoblaymiz : . Ichki integralni ajratib olib, hisoblaymiz: . Oxirgi ifodada Eylerning ushbu , gipergeometrik integrali formulasidan foydalansak, bo’ladi. , . , bunda , . . , , Ichki integralni ajratib olib, hisoblaymiz : . . . . 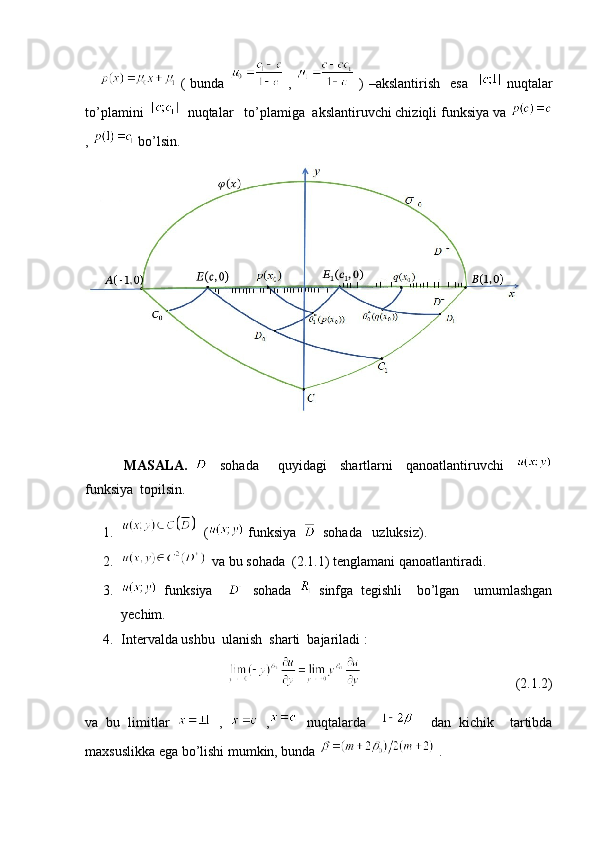Oxirgi tenglikda quyidagi formuladan foydalanib, shakl almashtirish bajaramiz: x = c . 1 − 2 β x = − 1 h ( c ) . τ0(x)−λ∫ −1 с ( 1+x 1+t) 1−2β ( 1 t−x − 1 1−xt)τ0(t)dt=g0(x), x∈(−1,c) g0(x)=λk ∫ c1 1 ( 1+x 1+q(t)) 1−2βτ1(t)dt q(t)−x+L1[τ1]+F5(x), x∈(−1,c) . . .+ L 3[τ1]+ F 6(x), x ∈ (− 1 ,c), , , . t = − 1 + ( 1 + x ) σ t = с − ( с − x ) σ . , , δ → 0 t = − 1 + ( 1 + c ) σ t = c − ( 1 + c ) σ. , τ0( x )= λk cos 2 απ ∫ c1 1 ( 1 + x 1 + q (t )) 4α τ1( t)dt q (t )− x + , − sin ( 2 απ ) 2 π π ctg ( απ )+ cos 2 απ = 0 τ0(x)=∫c1 1 K(x,t)τ1(t)dt +L3[τ1]+F6(x) x∈(−1,c) τ0(x) τ 1 ( x ) τ0( x )= L 4[τ1]+ F 0( x ) , x ∈ (− 1 ,c ) . , τ0(x) , F 7(x)= T [F6]+F 3(x) x = c 1 , t = c 1 . . x ∈ ( c 1 , 1 ) H x=1 x = с 1 . z Φ + ( a , x ). Φ − ( a , x ) Φ ( a , z ) z ( x , 0 ) Φ(a,1z)=azΦ(1a,z). w = 1 z ( c 1 , 1 ) Δ . Demak, 12 integral quyidagicha ekan: - regulyar operator. , ,x , 1 x , Φ + ( 1 a ,x)(1+ λπ i)− Φ − ( 1 a ,x)(1− λπ i)= − 1 ax g( 1 x), x∈ Δ . , Φ + ( x )− G (x )Φ − ( x )= h (x ), x ∈ (c1,1 )∪ Δ , , , Φ ( z ) , ,z . Endi bu integrallarning qiymatlarini (3.1.2) tenglikka olib borib qo’yamiz: Χ ( z ) ( с 1 , 1 ) ∪ Δ , Χ + ( x )= G ( x ) Χ − ( x ), x ∈ ( с 1 ,1 )∪ Δ . Χ ( z )= exp {α ∫ c1 1 ( 1 t− z − z 1 − zt ) dt } Χ(z)=exp {α[2ln(1−z)−ln(c1−z)−ln(1−c1z)]} . Yuqoridagi tenglikda (2.1.6) shartga ko’ra deb olsak va ba’zi shakl almashtirishlar qilsak, quyidagi tenglik hosil bo’ladi: Φ +(x) X +(x) − Φ − (x) X −(x) = h(x) X +(x) , x∈ (c1,1 )∪ Δ ., (3.1.3) bu yerda t 1 t , Φ(z) X(z)= 12πi[∫c1 1 g(t)dt (1−λπi)X+(t)(t−z)+∫c1 1 a−1g(t)dt (1+λπi)X+(1t)(1−tz)]. deb olsak, Φ + ( x ) X + ( x ) − Φ − ( x ) X − ( x ) = 0 . . χ ( z ) = Φ ( z ) X ( z ) z = c 1 , z = 1 , . χ ( z ) = α 1 z − c 1 + α 2 z − 1 . , bu yerda . X − ( x ) . X + ( x ) - regulyar operator bo’lganligi uchun (3.1.2) tenglik quyidagi ko’rinishni oladi: , bu yerda x = 1 . Oxirgi tenglikni har ikkala tomonini ρ ( x ) ga ko’paytiramiz: x = c 1 . Oxirgi tenglikda α1=0, α2= 0, deb belgilash kiritsak, quyidagi singulyar integral tenglama hosil bo’ladi: tenglama hosil bo’ladi. Bunda x = c 1 . (3.1.2) tenglik tufayli va и k = b , ρ = a dan (3.1.3) tenglama quyidagi ko’rinishga ega: τ 1 ( x ) + λ ∫ c1 ( 1 − x 1 − t ) 1 − 2 β ( 1 t − x + b 1 − ( bx − a )( bt − a )) τ 1 ( t) dt = g 0 ( x ) , (3.1.4) где R1[τ1]= R[τ]− λ∫c 1 ( 1− x 1−t) 1−2β R0(x,t)dt ,λ= cos (βπ ) π(1+sin βπ ).Vaqtinchalik, (3.1.4) tenglamaning o’ng tomonini ma’lum funksiya deb hisoblaymiz:. (3.1.4) tenglamani quyidagi ko’rinishda yozamiz: τ1(x)+λ∫c 1 ( 1− x 1− t) 1−2β ( 1 t− x+ b 1−(bx −a)(bt − a))τ1(t)dt= g0(x),(33 1) где g 0 ( x ) = a 0 b k 2 β a 0 + b 0 λ ∫ c1 ( 1 − x 1 − t ) 1 − 2 β τ 1 ( t) dt 1 − bx − at + ¿ . +b0ak−2β a0+b0 λ∫c 1 ( 1− x 1−t) 1−2β τ1(t)dt 1−ax − bt +R1[τ1]+F1(x), 3.2-§. Singulyar integral tenglamani regulyarizatsiyalash ρ ( x ) = ( 1 − x ) 2 β − 1 τ 1 ( x ) , g ( x ) = ( 1 − x ) 2 β − 1 g 0 ( x ) . ρ ( x ) + λ ∫ c1 ( 1 t − x + b 1 − q ( x ) q ( t)) ρ ( t) dt = g 0 ( x ) , ( 3 .2 .1 ) z -kompleks tekislikdagi ixtiyoriy nuqta. Karleman metodidan foydalanamiz: Φ ( z ) = 1 2 πi ∫ c1 ( 1 t − z + b 1 − ( a − bz )( a − bt )) τ ( t) dt . Φ ( 1 + a + az bz − a ) = ( a − bz ) Φ ( z) = − ( bz − a ) Φ ( z ) . ( 3 .2 .2 ) Ushbu kasr chiziqli almashtirishdan foydlanamiz: w= 1+a+az bz −a . Δ= { (−∞ ,−1)∪( −2+c 2 ,+∞),если c<0 (− ∞ ,−1),если c=0 ( −2+c c ,−1),если c>0 Φ+¿(x)−G(x)Φ−¿(x)=H(x),−∞<x<∞(3.2.3)¿¿ где G( x ) = { 1 − λπi 1 + λ π i = e − 2 απi , если x ∈ ( c , 1 ) 1 + λπi 1 − λπi = e 2 απi , если x ∈ Δ 1 , если x ∉ ( − 1,1 ) ∪ ∆ H (x)= { g(x) 1+λπi ,если x∈(c,1) g( 1+a+ax bx −a ) 1 (1− λπi )(bx −a)=e2απi ,если x∈Δ 0,если x∉c∪∆. (3.2 .4) (3.2.1) ni Riman masalasini yechish nazariyasiga ko’ra sakrash maslasiga tushiramiz . Buning uchun G ( x ) ni faktorizatsiyalangan ko ’ rinishda yozamiz : X + ¿ ( x) − G ( x) X − ¿ ( x) = 0 , ( 3.2 .5 ) ¿ ¿ (3.2.5) shart bilan sakrash masalasining maxsus yechimlaridan biri X ( z ) = exp { 1 2 πi ∫ c1 ( 1 t − z + b ( bz − a ) 1 − ( bz − a )( bt + a )) ln G ( t ) dt } . X ( 1 + a + a z bz − a ) = X ( z ) . Shunday qilib , (3.2.5) ga ko ’ ra (3.2.4) chegaraviy shartni quyidagi ko ’ rinishda yozamiz : Φ + ¿ ( x) X + ¿ ( x) − Φ − ¿ ( x) X − ¿ ( x) = H ( x ) X + ¿ ( x) . ( 3.2 .6 ) ¿ ¿ ¿ ¿ ¿ Φ (z) X (z)= 1 2πi ∫−∞ +∞ H (t) X+¿(t) dt t− z+ c0 1− z+ c1 1+z¿ yoki Φ ( z ) = X ( z ) 2 πi ∫ − ∞+ ∞ H ( t) X + ¿ ( t) dt t − z + X ( z)( c 0 1 − z + c 1 1 + z ) . ¿ Φ ( z ) yechimni H ( t) = 0 , t ∉ ( − 1,1 ) ∪ ∆ larni hisobga olgan holda yozamiz: Φ (z)= X(z) 2πi ∫c 1 H (t) X+¿(t) dt t− z+X (z) 2πi ∫∆ ❑ H (t) X+¿(t) dt t− z+X (z)( c0 1− z+ c1 1+z).(42 )¿¿ Φ (z)= X (z) 2πi ∫c 1 g(t) eαπi X+¿(t) dt t− z+ X (z) 2πi ∫∆ ❑ H (t) e−απi (bt − a)X+¿(t) dt t− z+¿¿¿ + X( z )( c 0 1 − z + c 1 1 + z ) . Ikkinchi integralda (3.2.6) o’zgaruvchining o’zgarishi t = w ( s) = 1 + a + as bs − a , ni va w ( w ( s)) = s ni hisobga olgan holda, t= w(s):∆→ (c,1) (s= w(t)) , dt = − ds ( bs − a ) 2 , bw ( s) − a = 1 bs − a , w ( s) − z = 1 − ( bz − a ) ( bs − a ) b ( bs − a ) X + ¿ ( w ( s ) ) = X − ¿ ( s) =( G ( s ) ) − 1 X + ¿ ( s) = e − ( − 2 απi ) X + ¿ ( s) = e 2 απi X + ¿ ( s) ¿ ¿ ¿ ¿ ¿ olamiz. Φ (z)= X (z) 2πi ∫c 1 g(t) eαπi X+¿(t) dt t− z+ X (z) 2πi ∫1 c g(s)( −ds (bs −a)2) e−απi (bw (s)− a)X+¿(w(s)) 1 w(s)− z+¿¿¿ +X (z)( c0 1− z+ c1 1+z)= X (z) 2πi ∫c 1 g(t) eαπi X+¿(t) dt t− z+¿¿ +X (z) 2πi ∫1 c bg (s)ds (1−(bz − a)(bs −a))eαπi X+¿(s)+X (z)( c0 1− z+ c1 1+z)=¿¿ ¿X (z) 2πi 1 eαπi ∫c 1 g(t) X+¿(t)( 1 t− z+ b 1−(bz −a)(bt −a))dt +X (z)( c0 1− z+ c1 1+z)¿ Bizga ma’limki Saxotskiy-Plemeli formulasiga ko’ra ρ ( x ) = Φ + ¿ ( x) − Φ − ¿ ( x) = g ( x) 2 X + ¿( x) e απi ¿ ¿ ¿ ¿ +1 2πie απi ¿ +¿ yoki ρ ( x ) = g ( x ) 2 e απi ¿ + X + ¿ ( x) 2 πie απi ¿ ¿ +X+¿(x)¿¿ tenglikni hisobga olgan holda 1 e απi ¿ ga ega bo’lamiz. ρ( x ) = g ( x ) cos ( απ ) − X + ¿ ( x) sin ( απ) πi ∫ c1 g ( t) X + ¿ ( t) ¿ ¿ ¿ + b 1 − ( bx − a )( bt − a )) dt + ¿ Bu yerda X + ¿ ( x) ¿ va X−¿(x)¿ ni , (3.2.6) ifodalarni hisobga olsak, ρ ( x ) = g ( x ) cos ( απ ) − sin ( απ ) π ∫ c1 ( x − c t − c ) 2 α ( ( 1 − t )( 1 − c )( bt − a ) ( 1 − x )( 1 − c ( bx − a ))) α ∙ ∙ ¿ −isin (απ ) bα(x−c)2α (1− x)α(1− c(bx − a))α( c0 1− x+ c1 1+x) Bu yerda ρ ( x ) = ( 1 − x ) 2 β − 1 τ 1 ( x ) , g ( x ) = ( 1 − x ) 2 β − 1 g 0 ( x ) ni hisobga olgan holda , quyidagi formulalarga ega bo’lamiz: τ 1 ( x ) = g 0 ( x ) cos ( απ ) − sin ( απ ) π ∫ c1 ( x − c t − c ) 2 α ( 1 − x 1 − t ) 3 α ( ( 1 − c ( bt − a )) ( 1 − c ( bx − a ))) α ∙ ∙¿ − i sin ( απ ) b α ( 1 + x ) 2 α ( 1 − x ) 3 α ( 1 − c ( bx − a )) α ( c 0 1 + x + c 1 1 − x ) ( 3 .2 .7 ) τ 1 ( x ) uzluksiz funksiya bo’lganligi uchun , (3.2.7) formulada c0= 0,c1=0. ni qo’yishimiz kerak. Shunday qilib , τ 1 ( x ) = g 0 ( x ) cos ( απ ) − sin ( απ ) π ∫ c1 ( x − c t − c ) 2 α ( 1 − x 1 − t ) 3 α ∙ ∙ ( ( 1 − c ( bt − a )) ( 1 − c ( bx − a ))) α ¿ 3.3-§. Viner-Hopf integral tenglamasini hosil qilish (3.2.4) tenglamani o’rganishni davom ettiraylik. (3.2.2) dan (3.2.11) yechimga almashtirsak, τ1(x)=[ a0bk2β a0+b0 λ∫c 1 ( 1− x 1− s) 4α τ1(s)ds 1− bx −as +¿ +b0ak−2β a0+b0 λ∫c 1 ( 1− x 1− s) 4α τ1(s)ds 1−ax − bs +R1[τ1]+F1(x)]cos (απ )−¿ −sin (απ ) π ∫c 1 ( x−c t−c) 2α ( 1− x 1−t) 3α ∙( (1− c(bt− a)) (1− c(bx − a))) α ¿ − b 1−(bx − a)(bt −a))[ a0bk2β a0+b0 λ∫c 1 ( 1− x 1−s) 4α τ1(s)ds 1− bx −as +¿ +b0ak−2β a0+b0 λ∫c 1 ( 1− x 1− s) 4α τ1(s)ds 1−ax − bs +R1[τ1]+F1(x)]dt ,(3.3 .1)где k = a b . (3.3.1) da tenglamaning xarakterli qismini ajratib, uni quyidagicha yozamiz: τ 1 ( x ) = a 0 b k 2 β λ cos ( απ ) a 0 + b 0 ∫ c1 ( 1 − x 1 − s ) 4 α τ 1 ( s) ds 1 − bx − as + ¿ + b 0 a k − 2 β λ cos ( απ ) a 0 + b 0 ∫ c1 ( 1 − x 1 − s ) 4 α τ 1 ( s) ds 1 − ax − bs − ¿ − a 0 b k 2 β λsin ( απ ) π ( a 0 + b 0 ) ∫ − 11 ( x − c t − c ) 2 α ( 1 − x 1 − t ) 3 α dt t − x ∙ ∫ c1 ( 1 − t 1 − s ) 4 α τ 1 ( s) ds 1 − bt − as − ¿ +b0ak−2βλsin (απ ) π(a0+b0) ∫c 1 ( x−c t− c) 2α ( 1− x 1−t) 3α dt t− x∙ ∙∫c 1 ( 1−t 1− s) 4α τ1(s)ds 1−bt − as +R2[τ1]+F2(x),(3.3 .2) где R 2 [ τ 1 ] = R 1 [ τ 1 ] − sin ( απ ) π ∫ c1 ( x − c t − c ) 2 α ( 1 − x 1 − t ) 3 α ∙ ( ( 1 − c ( bt − a )) ( 1 − c ( bx − a ))) α ¿ − b 1−(bx − a)(bt −a))R1[τ1]dt +a0b2k2βλsin (απ ) π(a0+b0) ∫c 1 ( x−c t− c) 2α ( 1− x 1−t) 3α ∙ ∙( (1− c(bt − a)) (1− c(bx − a))) α dt 1−(bx − a)(bt − a)∙∫c 1 ( 1−t 1− s) 4α τ1(s)ds 1−bt − as +¿ +b0ab k−2βλsin (απ ) π(a0+b0) ∫c 1 ( x−c t− c) 2α ( 1− x 1−t) 3α ( (1− c(bt − a)) (1−c(bx − a))) α ∙ ∙ dt 1− (bx − a)(bt −a)∫c 1 ( 1−t 1− s) 4α τ1(s)ds 1− at− bs − ¿ −a0bk2βλsin (απ ) π(a0+b0) ∫c 1 ( x−c t− c) 2α ( 1− x 1−t) 3α [( (1− c(bt − a)) (1− c(bx − a))) α −1]∙ ∙ dt t − x ∫ c1( 1 − t 1 − s ) 4 α τ 1 ( s) ds 1 − bt − as − b 0 a k − 2 β sin ( απ ) π ( a 0 + b 0 ) ∫ c1 ( x − c t − c ) 2 α ( 1 − x 1 − t ) 3 α ∙ ∙[( (1−c(bt −a)) (1−c(bx −a))) α −1] dt t− x∫c 1 ( 1−t 1− s) 4α τ1(s)ds 1−at − bs - regulyar operator , F 2 ( x ) = cos ( απ ) F 1 ( x ) − sin ( απ ) π ∫ c1 ( x − c t − c ) 2 α ( 1 − x 1 − t ) 3 α ( ( 1 − c ( bt − a )) ( 1 − c ( bx − a ))) α ∙ ∙ ( 1 t − x − b 1 − ( bx − a )( bt − a )) F 1 ( t) dt -ma’lum funksiya. Integrallash tartibini o’zgartirgan holda (46) tenglamaning karrali integrallarini yozamiz: τ1(x)= a0bk2βλcos (απ ) a0+b0 ∫c 1 ( 1− x 1− s) 4α τ1(s)ds 1−bx −as +¿ + b 0 a k − 2 β λ cos ( απ ) ∫ c1 ( 1 − x 1 − s ) 4 α τ 1 ( s) ds 1 − bx − as − ¿ −a0bk2βλsin (απ ) π(a0+b0) ∫c 1 τ1(s)ds (1− s)4α(1+x)2α(1− x)3α∫c 1 (1−t)α (1+t)2α 1 t− x∙ ∙ dt 1− bt −as − b0ak−2βλsin (απ ) π ∫c 1 τ1(s)ds (1− s)4α(1+x)2α(1− x)3α∙ ∙ ∫ c1 ( 1 − t ) α ( 1 + t ) 2 α 1 t − x dt 1 − at − bs + R 2 [ τ 1 ] + F 2 ( x ) , x ∈ I ( 3.3 .3 ) Bu yerda ichki integrallarni hisoblaymiz: A ( x , s ) = ∫ c1 ( 1 − t ) α ( 1 + t ) 2 α 1 t − x dt 1 − bt − as ( 48 ) ∫c 1(1+t)α1−1(1−t)β1−1 t− x dt = πctg (β1π) (x)− c1−α1(1− x)1−β1−¿ − 2 β 1 − 1 B ( α 1 , β 1 − 1 ) ( x − c ) 1 − α 1 F ( α 1 , 1 − β 1 , 2 − β 1 ; 1 − x 2 ) ( 3.3 .4 ) ∫−1 1 (1+t)α1−1(1−t)β1−1 1− at −bs dt = π sin (β1π) bβ1−1a1−α1−β1 (1+a+bs )1−α1(1− s)1−β1+¿ +a1−α1−1B(α1,β1− 1) 21−β1b(1+a−bs )1−α1F(α1,1− β1,2− β1;− b(1− s) 2a ).(3.3 .5)(3.3.3) da integralninng ratsional qismi oddiy kasrlarga ajratiladi: 1 t − x 1 1 − bt − as = ( 1 t − x + b 1 − bt − as ) 1 1 − bx − as A ( x , s ) = ∫ − 11 ( 1 − t ) α ( 1 + t ) 2 α 1 t − x dt 1 − bt − as = 1 1 − bx − as [ ∫ − 11 ( 1 − t ) α ( 1 + t ) 2 α dt t − x + ¿ + b ∫ − 11 ( 1 − t ) α ( 1 + t ) 2 α dt 1 − bt − as ]( 3.3 .6 ) (3.3.4) va (3.3.5) formulalardan α1−1=−2α,α1=1−2α, β1−1= α,β1= 1+α ni topamiz. A(x,s)= 1 1− bx −as [ πctg (1+α)π (1+x)2α(1− x)−α−¿ − 2 α B ( 1 − 2 α , α ) ( 1 + x ) 2 α F ( 1 − 2 α , − α , 1 − α ; 1 − x 2 ) + ¿ +πb sin (1+α)π bαaα−1 (1+a+bs )2α(1− s)−α+¿ + a2αB(1−2α,α) 2−αb(1+a−bs )2αF(1−2α,−α,1−α;− b(1− s) 2a )]. 1 ( 1 + x ) 2 α F ( 1 − 2 α , − α , 1 − α ; 1 − x 2 ) = ¿ ¿(1− 1− x 2 ) −2α 2−2αF(1−2α,− α,1−α;1− x 2 ),(3.3 .7) ( 1 1 + a − bs ) 2 α F ( 1 − 2 α , − α , 1 − α ; − b ( 1 − s ) 2 a ) = ¿ ¿(1+b(1− s) 2a ) −2α (2a)−2αF(1−2α,−α,1− α;− b(1− s) 2a ).(3.3 .8) (3.3.7) va (3.3.8) yordamida (3.3.6) tenglikni quyidagi shaklda yozamiz: A(x,s)= 1 1− bx −as [ πctg (απ )(1− x)α (1+x)2α − πb bαaα−1(1− s)α sin (απ )(1+a+bs )2α− ¿ − B ( 1 − 2 α , α ) 2 − α (( 1 − 1 − x 2 ) − 2 α F ( 1 − 2 α , − α , 1 − α ; 1 − x 2 ) − ¿ −( 1 − − b ( 1 − s ) 2 a ) − 2 α F ( 1 − 2 α , − α , 1 − α ; − b ( 1 − s ) 2 a ))]( 3.3 .9 ) ( 3.3.9 ) yordamida ( 3.3.6 ) tenglikni quyidagi ravishda yozamiz: τ 1 ( x ) = a 0 b k 2 β λ cos ( απ ) a 0 + b 0 ∫ − 11 ( 1 − x 1 − s ) 4 α τ 1 ( s) ds 1 − bx − as + ¿ +b0ak−2βλcos (απ ) a0+b0 ∫−1 1 ( 1− x 1− s) 4α τ1(s)ds 1− bx −as −¿ −a0bk2βλsin (απ ) π(a0+b0) ∫−1 1 τ1(s) (1− s)4α ds 1−bx − as ∙ ∙[πctg (απ )(1− x)4α− πb1+αaα−1(1− s)α(1− x)3α(1+x)2α sin (απ )(1+a+bx )2α −¿ − B(1− 2α,α) 2α (1− x)3α(1+x)2α ((1− 1− x 2 ) −2α F(1− 2α,− α,1−α;1− x 2 )−¿ −(1−− b(1− s) 2 ) −2α F(1−2α,−α,1−α;− b(1− s) 2a ))]−¿ − b 0 a k − 2 β λ sin ( απ ) π ( a 0 + b 0 ) ∫ − 11 τ 1 ( s) ds ( 1 − s ) 4 α ( 1 − bx − as ) ∙ ∙ [ π ctg ( απ )( 1 − x ) 4 α − a 1 + α b α − 1 ( 1 − s ) α( 1 − x ) 3 α ( 1 + x ) 2 α sin ( απ )( 1 + b + ax ) 2 α − ¿ − B(1− 2α,α) 2α (1− x)3α(1+x)2α ((1− 1− x 2 ) −2α F(1− 2α,− α,1−α;1− x 2 )−¿ − ( 1 − − a ( 1 − s ) 2 ) − 2 α F ( 1 − 2 α , − α , 1 − α ; − a ( 1 − s ) 2 b ))] + ¿ + R 2 [ τ 1 ] + F 2 ( x ) , x ∈ I ( 3.3 .10 ) Demak, cos (απ )−sin (απ )ctg (απ )= 0 ni hisobga olgan holda (3.3.10) tenglamani quyidagicha yozamiz: τ 1 ( x ) = − a 0 b k 2 β λ sin ( απ ) π ( a 0 + b 0 ) ( − π b 1 + α a α − 1 sin ( απ ) ) ∫ − 11 [( 1 + x 1 + a + bx ) 2 α − 1 + 1 ] ∙ ∙ ( 1 − x 1 − s ) 3 α τ 1 ( s) ds 1 − bx − as − b 0 a k − 2 β λ sin ( απ ) π ( a 0 + b 0 ) ( − a 1 + α b α − 1 sin ( α π ) ) ∙ ∙∫−1 1 [( 1+x 1+b+ax ) 2α −1+1]( 1− x 1− s) 3α τ1(s)ds 1−bx − as +¿ +R3[τ1]+F2(x),x∈I(3.3 .11 )bu yerda R3[τ1]= a0bk2βλsin (απ )B(1− 2α,α) 2απ(a0+b0) ∫−1 1(1− x)3α(1+x)2α (1− s)4α ∙ ∙ ¿ −(1−− b(1− x) 2 ) −2α F(1− 2α,−α,1− α;− b(1− x) 2a )] τ1(s)ds 1−bx − as +¿ +b0ak−2βλsin (απ )B(1− 2α,α) 2απ(a0+b0) ∫−1 1(1− x)3α(1+x)2α (1− s)4α ∙ ∙¿ − ( 1 − − a ( 1 − s ) 2 ) − 2 α F ( 1 − 2 α , − α , 1 − α ; − a ( 1 − x ) 2 b )] τ 1 ( s) ds 1 − ax − bs -regulyar operator, F 2 ( x ) -ma’lum funksiya. (3.3.11) ga binoan tenglamaning xarakterli qismini ajratib yozamiz: τ1(x)= a0bk2β−1λ(ab )α∫−1 1 ( 1− x 1− s) 3α τ1(s)ds 1− bx −as +¿ +b0ak1−2βλ(ab )α∫−1 1 ( 1− x 1− s) 3α τ1(s)ds 1−ax −bs +¿ + R 4 [ τ 1 ] + F 2 ( x ) , x ∈ I , ( 3.3 .12 ) bu yerda R 4 [ τ 1 ] = R 3 [ τ 1 ] + a 0 b k 2 β − 1 λ ( ab ) α a 0 + b 0 ∫ − 11 [( 1 + x 1 + a + bx ) 2 α − 1 ] ∙ ∙ ( 1 − x 1 − s ) 3 α τ 1 ( s) ds 1 − bx − as + b 0 a k 1 − 2 β λ ( ab ) α a 0 + b 0 ∙ ∙ ∫ − 11 [( 1 + x 1 + b + ax ) 2 α − 1 ]( 1 − x 1 − s ) 3 α τ 1 ( s) ds 1 − ax − bs . τ 1 ( x ) = λ ( ab ) α a 0 + b 0 ∫ − 11 ( 1 − x 1 − s ) 3 α ( a 0 b k 2 β − 1 1 − bx − as + b 0 a k 1 − 2 β 1 − ax − bs ) τ 1 ( s) ds + ¿ + R 4 [ τ 1 ] + F 2 ( x ) , x ∈ I , ( 3.3 .13 ) (3.3.13) tenglamada quyidagi belgilashlarni hisobga olsak, 1 − bx − as = b ( 1 − x ) + a ( 1 − s ) , 1 − ax − bs = a ( 1 − x ) + b ( 1 − s ) . τ 1( 1 − 2 e − y ) = λ ( ab ) α a 0 + b 0 ∫ − 11 e ( 1 2 − 3 α ) y e ( 1 2 − 3 α ) t( a 0 b k − 4 α b e − y 2 + t 2 + a e y 2 − t 2 + ¿ + b0ak4α ae −y2+t2+be y2−t2) τ1(1−2be−t)2dt +R4[τ1]+F2(1− 2e−y), Bu tenglamani e − ( 1 2 − 3 α ) y ga ko’paytiramiz: τ 1 ( 1 − 2 e − y ) e − ( 1 2 − 3 α ) y = λ ( ab ) α a 0 + b 0 ∫ − 11 ( a 0 b k − 4 α b e − ( y + t ) / 2 + a e ( y − t ) / 2 + ¿ + b 0 a k 4 α a e − ( y + t ) / 2 + b e ( y − t ) / 2) τ 1 ( 1 − 2 b e − t ) e − ( 1 2 − 3 α ) t dt + ¿ +e −(12−3α)y R4[τ1]+e −(12−3α)y F2(1−2e−y).(3.3 .14 ) bu yerda ρ(y)=τ1(1−2e−y)e −(12−3α)y K ( x ) = √ 2 π λ ( ab ) α a 0 + b 0 ( a 0 b k − 4 α b e − y 2 + t 2 + a e y 2 − t 2 + b 0 a k 4 α a e − y 2 + t 2 + b e y 2 − t 2 ) ( 3.3 .15 ) Viner-Hopf integral tenglamasini olamiz. ρ ( y ) = 1 √ 2 π ∫ 0+ ∞ K ( y − t ) ρ ( t ) dt + R 5 [ ρ ] + F 3 ( y ) , ( 3.3 .16 ) где R5[ρ]= e −(12−3α)y R4[τ1] -regulyar operator, F 3 ( y ) = e − ( 1 2 − 3 α ) y F 2 ( 1 − 2 e − y ) -ma’lum funksiya. Bunday tipidagi integral tenglamalar uchun Fredgolm teoremalari bu tenglamalarning indeksi nolga teng bo’lgandagina, faqat bitta holatda amal qiladi. K ∧ ( x ) = 1 √ 2 π ∫ − ∞+ ∞ e − ixt K ( t) dt = ¿ = λ ( ab ) α ∫ − ∞+ ∞ ( a 0 k − 4 α k e t 2 + e − t 2 + b 0 k 4 α k − 1 e t 2 + e − t 2 ) dt ( 3. .3 .17 ) ¿ Tenglikdan foydalansak, ∫−∞ +∞ e−ixtdt ke t2+e −t2 = πeixlnk √kch (πx )(3.3 .18 ) Bu yerda K ∧( x ) = λ ( ab ) α π a 0 + b 0 ( a 0 k − 4 α e ix ln k √ k + b 0 k 4 α √ k e − ix ln k ) 1 ch ( πx ) = ¿ ¿ λ ( ab ) α π √ k ( a 0 + b 0 )( a 0 k − 4 α e ix ln k + b 0 k 4 α k e − ix ln k ) 1 ch ( πx ) = ¿ ¿ λ(ab )απ √k(a0+b0)(a0k−4αcos (xln k)+ia0k−4αsin (xln k)+b0k4αkcos (xln k)−¿ − i b 0 k 4 α k sin ( x ln k )) 1 ch ( πx ) = λ ( ab ) α π √ k ( a 0 + b 0 )( a 0 k − 4 α + b 0 k 1 + 4 α ) cos ( x ln k ) ch ( πx ) + ¿ +i λ(ab )απ √k(a0+b0)(a0k−4α−b0k1+4α)sin (xln k) ch (πx ) Ko’rib chiqamiz: ℜ K ∧ ( x ) = λ ( ab ) α π a 0 + b 0 ( a 0 k − 4 α − 1 / 2 + b 0 k 4 α + 1 / 2 ) cos ( x ln k ) ch ( πx ) = ¿ ¿ λ ( ab ) α π a 0 + b 0 ( a 0 ( a b ) − 4 α − 1 / 2 + b 0 ( a b ) 4 α + 1 / 2 ) cos ( x ln k ) ch ( πx ) = ¿ ¿ λπ a 0 + b 0 ( a 0 a − 3 α − 1 / 2 b 5 α + 1 / 2 + b 0 a 5 α + 1 / 2 b − 3 α − 1 / 2 ) cos ( x ln k ) ch ( πx ) = ¿ ¿ λπ 22α(a0+b0)(a0(1+c)−3α−1/2(1−c)5α+1/2+¿ + b 0 ( 1 + c ) 5 α + 1 / 2 ( 1 − c ) − 3 α − 1 / 2 ) cos ( x ln k ) ch ( πx ) = ¿ ¿ λπ 22α(a0+b0)(a0(1+c)−3α−0,5(1−c)5α+0,5+¿ + b 0 ( 1 + c ) 5 α + 0,5 ( 1 − c ) − 3 α − 0,5 ) cos ( x ln k ) ch ( πx ) . Bu yerdan | ℜ K ∧ ( x )| ≤ λπ 2 2 α ( a 0 + b 0 )( a 0 ( 1 + c ) − 3 α − 0,5 ( 1 − c ) 5 α + 0,5 + ¿ +b0(1+c)5α+0,5 (1−c)−3α−0,5) 1 ch (πx ). bo’lsin. λπ 2 2 α( a 0 + b 0 )( a 0 ( 1 + c ) − 3 α − 0,5 ( 1 − c ) 5 α + 0,5 + ¿ +b0(1+c)5α+0,5 (1−c)−3α−0,5) 1 ch (πx )<1.(3.3.19 ) (3.3.19) tengsizlikni qanoatlantiruvchi b 0 = ( 1 − c ) 3 α + 1 masalaning sonli parametrlar to’plami bo’sh emas. Haqiqatan, (3.3.19) tengsizlikning chap tomoni birga yetarlicha yaqinlikdagi qiymatlar uchun (1− c)0,5 tartibli cheksiz kichik bo’lsin va shuning uchun masala parametrlarining bunday qiymatlari uchun (3.3.19) tengsizlik qanoatlantiriladi.. Shuning uchun |ℜ K ∧(x)|>0. Eslatib o ’ tamizki , agar z = x + iy kompleks o ’ zgaruvchi bo ’ lsa , va x >0 u holda , arg z = arctg y x . (41) dan ko ’ rinib turibdiki yetarli kichik |x|. lar uchun ℜ K ∧ ( x ) = 0 ( 1 / ch ( πx )) , ℑ K ∧ ( x ) = 0 ( 1 / ch ( πx )) lar o ’ rinli . Bundan kelib chiqadiki Ind (1− K ∧(x))= 1 2π[arg (1− K∧(x))]|−∞ +∞ = 1 2π[arctg ℑ(1− K∧(x)) ℜ (1− K∧(x))]|−∞ +∞ =¿ ¿ 1 2π[arctg 0 1− arctg 0 1]=0 Shunday qilib (3.3.16) tenglama Fredgolmning ikkinchi tur integral tenglamasiga bir qiymatli o’tkaziladi, yagonaligi esa asala yechimining yagonaligidan kelib chiaqdi. III bob bo’yicha xulosa Ushbu dissertatsiyaning 3-bobi singulyar koeffitsiyentli aralash tipdagi tenglama uchun tenglama tipi o’zgarish chizig’ida Frankl shartlili masalaning yechimining mavjudligiga bag’ishlangan. Dastlab va funksiyalar orasidagi birinchi va ikkinchi funksional munosabatlar keltirib chiqarilgan. Bunda shakli o’zgargan Koshi masalasining yechimi Darbu formulasidan foydalanilgan. Karrali integrallar hosil qilinib, ular mavjuda xossalar va teoremalar yordamida hisoblangan. Singulyar koeffitsiyentli tenglamaga olib kelingan va bu tenglama singulyar koeffitsiyentli tenglamani regulyarizatsiyalash usuli bilan ishlangan. Xulosa Mazkur magistrlik disertatsiyasi buzilish singulyar koeffitsiyentli buziluvchan turdagi tenglama uchun chegaraviy xarakteristikaning bir qismida Trikomi va ichki xarakteristikada siljishli shart berilgan masalani yechishga bag’ishlangan bo’lib, masala yechimining mavjudligi va yagonaligi isbotlangan. Unda olingan natijalardan quyidagi xulosa kelib chiqadi: 1.Bu dissertatsiyani yozishda gipergeometrik funksiya, kasr-tartibli integro- differensial operatorlar, elliptik tipdagi tenglamalar uchun ekstremum prinsipi batafsil o’rganib chiqildi. 2.Singulyar koeffitsiyentli buziluvchan turdagi tenglama uchun TI masala qo’yildi va uning yechimining yagonaligi isbotlandi. 3. TI masala yechimining mavjudligi keltirib chiqarildi. Ushbu magistirlik dissertatsiyasida olingan natijalardan singulyar koeffitsiyentli aralash tipdagi tenglamalar uchun chegaraviy masalalarni o’rganishda hamda bunday tenglamalarga keltiriladigan amaliy masalalarni yechishda foydalanish mumkin Foydalanilgan adabiyotlar ro’yxati I.Normativ-huquqiy hujjatlar 1. O’zbekiston Respublikasi prezidenti Sh.M. “Milliy taraqqiyot yo’limizni qat’iyat bilan davom ettirib, yangi bosqichga ko’taramiz”. Toshkent- “O’zbekiston”-2017-yil. 2. Mirziyoyev Sh.M. PQ-2909 sonli “Oliy ta’lim tizimini yanada rivojlantirish chora-tadbirlari to’g’risida”gi qarori. 2017-yil 20-aprel. II. Asosiy adabiyotlar 3. Смирнов М.М. Уравнения смешанного типа. М. : Наука. 1970 , -296 c. 4. Salohitdinov M. Matematika fizika tenglamalari. Toshkent-“O’zbekiston “ nashriyoti, 2002-yil. 448 b. 5. Mirsaburov M. Singulyar koeffitsiyentli Gellerstedt tenglamasi uchun Trikomi masalasi. Termiz-“Surxon-nashr” 224 b. 6. Salohitdinov M.S., O’rinov A.Q. Giperbolik va elliptik tipdagi buziladigan differensial tenglamalar. Toshkent-“Universitet”, 2006,270 b. 7. O’rinov A.Q. Maxsus funksiyalar va maxsus operatorlar. Farg’ona,2012,112 b. 8. Kilbas A.A., Srivastava H.M. and Trujillo Y.Y.Theory and applications of fractional differential equation. North Holland. “Math, Studies204. Amsterdam- Boston. Tokio. – 2006. –pp.523. 9. Салахитдинов М.С. , Мирсабуров М. Нелокальние задачи для уравнений смешанного типа с сингулярними коеффициентами. Тошкент. 10. Бицадзе А.В., Самарский А.А. О некоторых простейших обобщениях линейных эллиптических краевых задач // ДАН СССР, 1969. Т 185, № 4, С. 739- 740. 11. Нахушев А.М. О некоторых краевых задачах для гиперболических уравнений и уравнений смешанного типа. // Дифференциальные уравнения. 1969. Т. 5. № 1. С. 44 – 59. 12. М ирсабурова . Г . М . Комбинированние задачи с локалними и нелокалними краевими условиями для уравнения Геллерстедтас сингулярним коиффициентом - М. : Наука . 2024.79 c . III . Mavzu bo ’ yicha e ’ lon qilingan materiallar 1 . Краевая задача с локальными и нелокальным условием на частях граничной характеристики для одного класс уравнений смешанного типа «Современные проблемы дифференциальных уравнений и их приложения» Международная научная конференция Ташкент , 23-25 ноября 2023 года ТЕЗИСЫ ДОКЛАДОВ ЧАСТЬ I Современные проблемы дифференциальных уравнений и их I Ташкент-2023 47 страница. 2 A problem with a displacement on the internal characteristics in an unbounded domain for the Gellerstedt equation with singular coefficients. OF THE IX INTERNATIONAL SCIENTIFIC CONFERENCE "ACTUAL PROBLEMS OF APPLIED MATHEMATICS AN INFORMATION TECHNOLOGIES AL- KHWARIZMI 2024" Dedicated to the 630th anniversary of the birth of Mirzo Ulugbe 22-23 October, 2024, Tashkent, Uzbekistan Actual problems of applied mathematics and information technologies Al- Khwarizmi 2024 176 страница .

Buziluvchan  va aralash  turdagi  tenglamalar. Gipergeometrik funksiya, kasr-tartibli integro-differensial operatorlar, elliptik  tipdgi tenglamalar uchun ekstremum prinsipi

 

Купить