Дата регистрации 27 Январь 2024
852 ПродажEyler va Runge-Kutta usullari




![1 Birinchi tartibli oddiy differensial tenglamalarni chekli ayirmalari usuli
bilan taqribiy yechish
Masalani yechish:
Hosilaga nisbatan yechilgan quyidagi birinchi tartibli differensial tenglama
y
= f(
x y ) ( 2
. 1
. 1)
va uning boshlang’ich sharti
y (
xO = Уо (2.1.2)
berilgan bo’lsin.
Bu yerda x o’zgaruvchi [a:b] oraliqda kesmani x
t nuqtalar yordamida teng
uzoqlikdagi kesmalarga bo’lib chiqamiz, ya’ni oddiy tekis to’r olamiz:
w
h = {x. = ih, i = 1,2,3 ,..., N -1]
Kesmalarning uzunliklari h bo’lsin, ya’ni h = x, -x
n = x
9 -x, =... = x -x ,
1 о 2 1 n n- 1
Demak, h = b-a
= ——^
n n
Berilgan masalani chekli ayirmali masala ko'rinishiga keltirish uchun quyidagi
chekli ayirmali sxemadan foydalanishimiz mumkin:
y = Ум
+ Уг
- o'ng chekli ayirmali sxema. h
Qo'yilgan masalaga mos chekli ayirmali masalani yozamiz:
= f. i = о , 1 , 2 ,..., N - 1 ; у (-^ о ) = Уо (2.1.3)
Biz foydalangan chekli ayirmali sxemada (2.1.3) qo'yilgan masala (2.1.1 ni 0(h)
5](https://docx.uz/documents/dd3e9d9d-3b0f-4bcc-ae7d-9af1947cc5c1/page_5.png?v=1)
![aniqlikda approksimatsiyalaydi. (2.1.3) dan ko'rinib turubdiki, bizsa N ta
tenglamalar tizimi hosil bo'ladi : y,-=i = у, = hf
i = 0,1,..., N -1; y ( x
0 ) = y 0
Yuqoridagi keltirib chiqarilgan rekurrent formula (2.1.1) masalani yechimini
SHEHM larda hisoblash algoritmidan iborat bo'ladi. Bunday algoritm yordamida
(2.1.1) masalani 0(h) aniqlikdagi x
0 ,x ,...,x
n nuqtalarda taqribiy yechimini topish
mumkin. Haqiqatdan, shu shartni bajarilishini (2.1.1) masala aniq yechimini
sinash funksiyasi yordamida ko'rish bilan tekshirish mumkin. Sinov funksiyasi
tariqasida
S.Akbarova, A.Qodirov, „Differensial tenglamalardan masalalar to'plami” №264
xy -2 y = 2x 4
ni olishimiz mumkin. Ushbu tenglamani (2.1.1) masalaga qo'yib,
quyidagilarga esa bo'lamiz:
xy -2 y = 2x 4
ni o'zgarmasni variatsiyalash usulida har ikkala tomonni x ga bo'lib,
ushbu tenglikka keltiramiz:
y '-2 y
= 2x 3
va bu tenglamani chap tomonini 0 ga tenglab, bir jinsli ko'rinishga
x
keltirib olamiz:
У - 2 У
= 0 x
±
- 2y =
0
dx x
dy
= 2 y
dx x
ln y = 2ln x + ln c = ln x 2
+ ln c = ln ex 2
ln y = ln ex 2
y
b] = ex 2
bir jinsli qism yechildi.
yc(x)x 2
ni tenglamaga
qo’yamiz:
y ' = c (x) x 2
+ c(x)2x
c ' ( x) x 2
+ c( x)2 x - 2 c( x) x
= 2 x 3
6](https://docx.uz/documents/dd3e9d9d-3b0f-4bcc-ae7d-9af1947cc5c1/page_6.png?v=1)

![y
= y )
( 2 . 2 . 1 )
birinchi tartibli differentsial tenglamaning [a,b] kesmada boshlang’ich shart x=x 0
bo'lgan hol uchun y=y
0 ni qanoatlantiruvchi echimi topilishi lozim bo'lsin. [a,b]
kesmani x0 , x1, x2 ,. • •, xn nuqtalar bilan n ta teng bolakchalarga ajratamiz;
bunda
b - a
х = x
0 + ih (i= 0,1,2,_ n), h = --------- qadam.
n
(2.2.1) tenglamani [a,b] kesmaga tegishli bo'lgan biror [xk, Xk+ 1 ] kesmada
integrallasak,
8](https://docx.uz/documents/dd3e9d9d-3b0f-4bcc-ae7d-9af1947cc5c1/page_8.png?v=1)
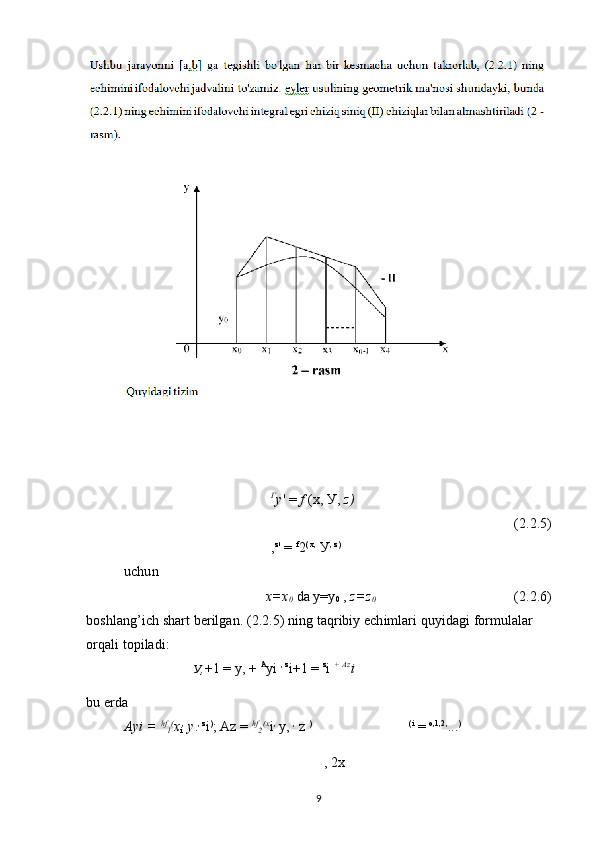
![Misol. eyler usuli yordamida у = у -------------- differentsial tenglamaning
у
[0,1] kesmada olingan va u(0)=1 boshlang’ich shartni qanotlantiruvchi u(x)
echimining taqribiy qiymatlarini h=0,2 qadam bilan toping.
Echish:
1 x
f (x, у) = у - - - - - - ; a = о, b = 1, Xo = о, Уо = 1, h = о,2
У
Quyidagi hisoblash jadvalini to'zamiz.
1- qator .
i=0, x
0 = 0, y
0 = 1,0000
2 r 9*0
f ( Г 0, y 0) = y 0 ----- 0
= 1 ----- — = 1,0000
У 0 1
Ay 0 = hf ( Г 0, y 0) = 0 , 2*1 = 0,2000
yi +1 = yi + A
yi ,
i = 0
; y1 = y 0 + A
y 0 = 1
+ 0 , 2
= 1 , 2 0 0 0
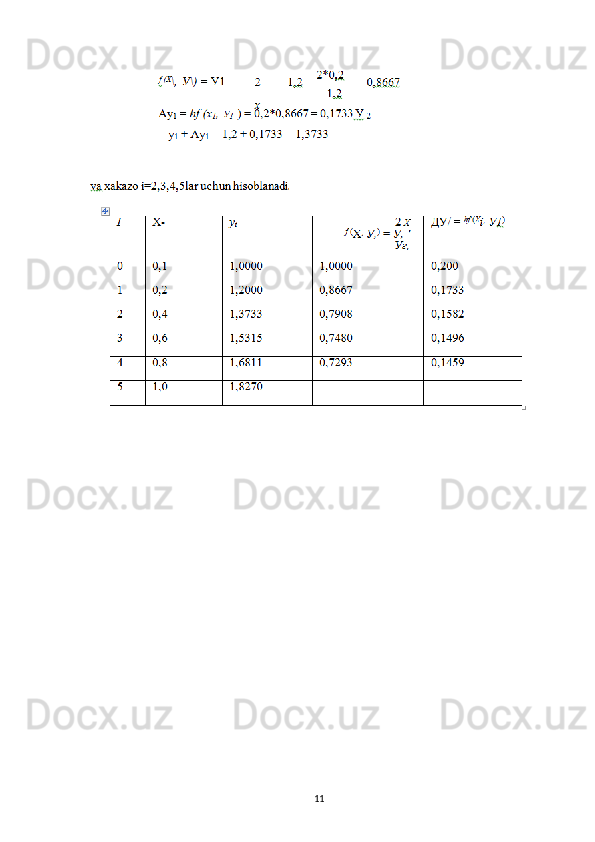
2- qator.
i=1 , r = 0 + 0,2 = 0,2; y
l = 1,2000;
10](https://docx.uz/documents/dd3e9d9d-3b0f-4bcc-ae7d-9af1947cc5c1/page_10.png?v=1)
![Runge-Kutta usuli
Runge - Kutta usuli ko'p jihatdan Eyler usuliga o'xshash, ammo aniqlik
darajasi eyler usuliga nisbatan yuqori bo'lgan usullardan biridir.
Runge-Kutta usuli bilan amaliy masalalarni echish juda qulay. CHunki, bu
usul orqali noma'lum funktsiyaning x
i+ i dagi qiymatini topish uchun uning xt dagi
qiymati aniq bo'lishi etarlidir. Runge-Kutta usuli uning aniqlash darajasiga ko'ra
bir necha turlarga bo'linadi. Shulardan amaliyotda eng ko'p qo'llaniladigani
to'rtinchi daraja aniqlikdagi Runge-Kutta usulidir.
Birinchi tartibli y=f(x,y) differentsial tenglama uchun x=xt
(i=0,1,2,...n)y=yt ma'lum bo'lsin. Bu erda y
t boshlang’ich shart ma'nosida
bo'lmasligi ham mumkin. Noma'lum funktsiya y ning x=x
i +
1 dagi qiymati
y
i +
1 =y
i +
1 (x) ni topish uchun quyidagi ketma-ket hisoblash jarayonini amalga
oshirmoq lozim bo'ladi:
x
,+1 = x
, + h
y
t +1 = y
t + А
у, >
Ay, = + 2$° + 263'’ + Q )
], 6
12](https://docx.uz/documents/dd3e9d9d-3b0f-4bcc-ae7d-9af1947cc5c1/page_12.png?v=1)
![h O m
Of = hf(x
0 + -, y + O-) = 0,1* f (1,85;2,7006) = 0,2205,2 2
O4 0)
= hf (Х 0 + h, y 0 + O
3 <0)
) = 0,1 * f (1,9;2,6099) = 0,2927,
У1 = У 0 + 1
[Oi (0)
+ ZQf' + O4 0)
] = 2,0259,
6
i = 1; x
1 = 1,9; y
1 = 2,0259; y
2 = 3,0408 va hokazo.
13](https://docx.uz/documents/dd3e9d9d-3b0f-4bcc-ae7d-9af1947cc5c1/page_13.png?v=1)
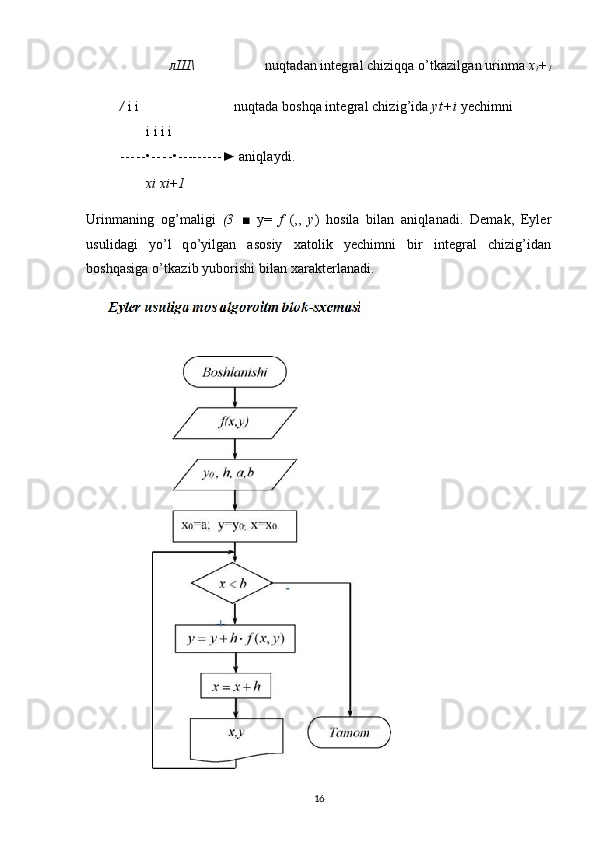
![Sonli differensiallash va differensial hisoblash uchun dasturlar tuzish
Eyler usulining ishchi algoritmi ishlab shiqish
Bizga quyidagi birinchi tartibli differensial tenglama(Koshi masalasi)ni
[a,b] oraliqdagi y 0 =y(X 0 ), X 0 =a boshlang’ich shartni qanoatlantiruvchi yechimini
topish lozim bolsin.
Koshi masalasini Eyler usuli yordamida yechish uchun, dastlab differensial
tenglamaning yechimi qidiriladigan [a,b] kesmani X 1 ,X 2 ,...Xn tugun nuqtalar
bilan bolaklarga bolamiz. Tugun nuqtalarning koordinatalari X
i+1 =a+(i+1)h
(i=0..n-1) formula orqali aniqlanadi. Har bir tugunda y(Xi) yechimning
qiymatlarini chekli ayirmalar yordamida taqribiy y i qiymatlar bilan almashtiriladi.
(2) differensial tenglamani Xi nuqta uchun yozib y’(Xi) =f(Xi, y(Xi)) olib,
y ( x ) « y(x
+ i) - y(x)
chekli ayirmali formuladan foydalanamiz va natijada quyidagi
h
Eyler formulasiga ega bo’lamiz:
14](https://docx.uz/documents/dd3e9d9d-3b0f-4bcc-ae7d-9af1947cc5c1/page_14.png?v=1)


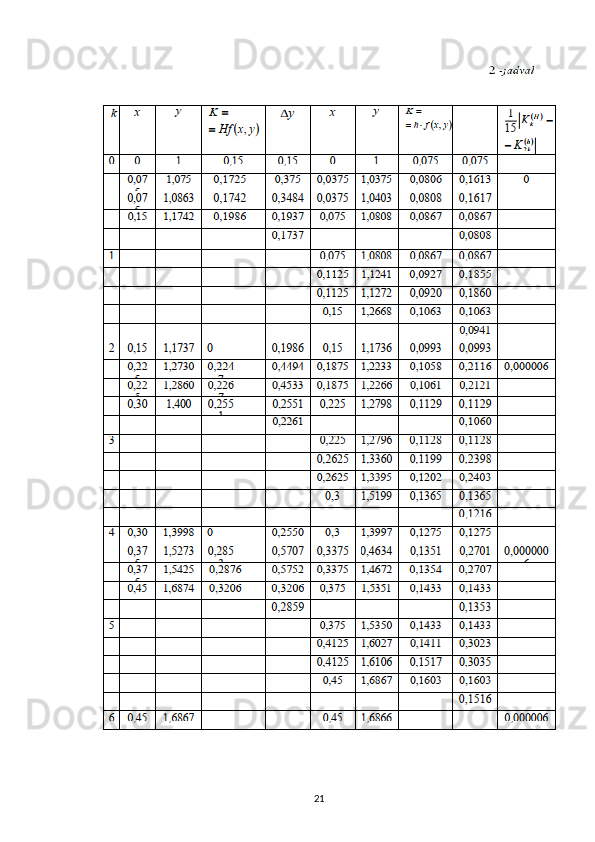
![Dasturdan olingan natijalar va ularning tahlili
Endi biz yuqorida keltirilgan algoritmlar asosida tuzilgan dasturlarning
to’g’riligini va usullarning aniqlik darajasini tekshirish uchun bitta ixtiyoriy
tenglama olamiz.
Aniq yechimni analitik usulda hisoblash qulay bo’lishi uchun quyidagi
tenglamani ko’rib chiqamiz.
y’=cosx tenglamani [0,1] oraliqda h=0.1 qadam bilan y(0)=1 boshlang’ich shartni
qanoatlantiruvchi yechimni topish kerak.
Yuqoridagi dasturlarga kerakli qiymatlarni kiritamiz. x
0 = 0; y
0 = 1;
f (x) = cosx; a = 0; b = 1; h = 0.1
y’=cosx uchun aniq yechim sifatida y = sinx + с ni olamiz. Boshlang’ich
shartlarni qo’ysak, 1=sin0+c =1 Demak, y=sinx+1. Endi biz datur yordamida
18](https://docx.uz/documents/dd3e9d9d-3b0f-4bcc-ae7d-9af1947cc5c1/page_18.png?v=1)








Eyler va Runge-Kutta usullari