Информация о документе

Цена 12000UZS
Размер 584.6KB
Покупки 7
Дата загрузки 15 Декабрь 2024
Расширение docx
Раздел Курсовые работы
Предмет Алгебра

Продавец

Bahrom

Дата регистрации 05 Декабрь 2024

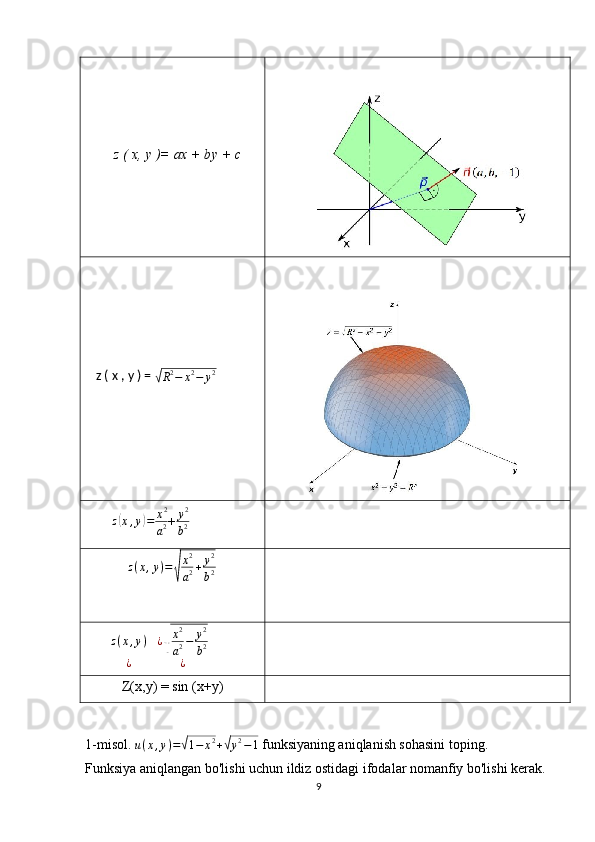
246 Продаж

Ko’p o’zgaruvchili funksiyalar

Купить
O‘ZBEKISTON RESPUBLIKASI OLIY TA’LIM, FAN VA INNOVATSIYALAR VAZIRLIGI __UNIVERSITETI Ro’yxatga olindi №__________ Ro’yxatga olindi №__________ “_____” ____________20 y. “_____” ____________20 y. “___________________________ “ KAFEDRASI “_____________________________ “ FANIDAN KURS ISHI Mavzu:________________ Bajardi:_________________________________ Tekshirdi:_______________________________ ______________ - 20___ Ko’p o’zgaruvchili funksiyalar MUNDARIJA Kirish……………………………………………………………………………...3 I BOB. KO’P O’ZGARUVCHILI FUNKSIYALAR 1.1-§. Ko‘p o‘zgaruvchili funksiya tushunchasi …………………........................5 1.2-§. Rm fazoda ketma-ketlik va uning limiti ….................................................10 1.3-§. Ko’p o’zgaruvchili funksiya va uning limiti....………………...................12 II BOB. KO’P O’ZGARUVCHILI FUNKSIYALARNING UZLUKSIZLIGI. 2.1 -§ Ko’p o’zgaruvchili funksiyalarning uzluksizligi..........................................23 2.2-§ Uzluksizlik funksiyalarning xossalari...........................................................25 2.3-§ Ko’p o’zgaruvchili funksiyaning tekis uzluksizgi. Kantor teoremasi...........27 Xulosa……………………………………………………………………….........30 Foydalanilgan adabiyotlar………………………………………………………...32 3 KIRISH Davlat ta’lim standarti o’quvchilarning har biriga ta’lim olishda keng imkoniyatlarni yaratib berish,har birining yuqori natijaga erishishlarini rag’batlantirish va shu orqali o’quv – biluv jarayonining farqli tashkil etilishini ta’minlash uchun da’vat etilgan Yuqorida aytilgan mezon va talablarga rioya qilgan holda. Respublikamizda, zamonaviy bilim malaka va ko’nikmalarga ega va yosh avlodni tarbiyalashda zamonaviy metod va uslublardan foydalana oladigan yetuk kadrlar tayyorlash dolzarb vazifalardan hisoblanadi. Shu borada, hech shubhasiz, o’z vaqtida, ya’ni bundan 20-yil oldin Kadrlar tayyorlash va shuningdek, maktab ta’limini rivojlantirish umummilliy dasturlarni qabul qilganimiz ta’lim - tarbiya sohasida eski qolip va asoratlardan holi bo’lgan, bugun o’zgalarning havasini tortayotgan yangi tizimni hayotimizda tadbiq etganimiz haqiqatdan ham tarixiy bir voqea bo’ldi, desak, adashmagan bo’lamiz. Buning natijasida mustaqil va yangicha fikrlaydigan, zamon talabiga javob beradigan avlodni shaklantirishga erishdik, Vatanimizning ertangi kunini, taqdirini o’z qo’liga olishga qodir bo’lgan farzndlarimiz bugun minbarga chiqmoqda. Ma’lumki, Davlat ta’lim standartlarida uzluksiz ta’lim tizimining har bir mustaqil ta’lim turi boshqa ta’lim turlari va bosqichlari bilan uzluksizlik va uzviylik tamoyillariga asosan bog’lanishi ko’zada tutilgan.Shu o’rinda har bir ta’lim turi va bosqichi o’ziga xos xususiyatlarga ega bo’lib, oldingisidan keyingisiga o’tishda ta’lim jarayoni samarali kechishi uchun o’qituvchi va o’quvchidan alohida tayyorgarliklarni talab etishi aniq. Bunday muammolar asosan o’rta maxsus, kasb – hunar va oliy ta’lim muassasalar o’rtasidagi ta’lim mazmuni va jarayonini tashkil etishdagi uzluksiz va uzviylik masalasini hal etishda 4 mavjuddir. Bu borada matematika fani katta imkoniyatlarga ega. Shunday ekan, matematika fani izchil, bosqichma – bosqich boshqa fanlar bilan aloqadorlikda o’rganish o’quvchilar mustaqil fikrlash qobiliyatini o’stirishga yordam beradi. Respublikamizda matematika fani asoslari turli bosqichlarda faoliyat ko’rsatayotgan ta’lim muassasalarining ta’lim mazmuniga mos ravishda o’quvchilarning psixologik va pedagogok xususiyatlariga muvofiq muayyan izchillikni o’rnatish fanlar, boblar, mavzular, o’quv materiallari orasida uzviylikni ta’minlash asosida amalga oshiriladi. Shunday ekan, matematika fani asoslarini yorituvchi kurslar o’rtasida uzviylikni ta’minlash, o’quv materiallarini turli bosqich ta’lim muassasalari o’quvchilarining yosh xususiyatlariga mos holda tanlash, ularning muayyan mantiqiy ketma – ketlik, fanlararo uzviylik hamda izchillik asosida joylashtirish, o’quv jarayonida uzviylik tamoyilining yetakchi o’rin tutishiga erishish va bu holatni pedagogik jihatdan asoslash muammosini yuzaga keltiradi. Kurs ishi mavzusining dolzarbligi: Ko`p o`zgaruvchili funksiya matematik analizning asosiy masalalaridan biri bo’lib, faqatgina geometriya, fizika masalalarini hal etishda emas, balki texnika fanlarining ko’pgina sohalaridagi masalalarni hal qilishda ishlatiladi. Shuning uchun kurs ishining mavzusi va o’zi dolzarb Kurs ishining maqsadi : ko’p o’zgaruvchili funksiyalari haqida matematik analiz darslarida o’rganilgan tushuncha va tasdiqlarni mustahkamlash va amaliyotda qo’llashdir. Kurs ishining vazifasi: ko’p o’zgaruvchili funksiyalar tushunchasini tushunish va ularning oblasti aniqlash; ko’p o’zgaruvchili funksiyalarning uzluksizligi, 5 chegaralari va ekstremumlari haqida bilish; ko’p o’zgaruvchili funksiyalarning xosilasi va differensialini topish va ularning xossalari haqida bilish. I bob. Ko’p o’zgaruvchili funksiyalar 1.1 . Ko‘p o‘zgaruvchili funksiya tushunchasi. Faraz qilaylik, m R fazoda E to‘plam berilgan bo‘lsin: mR E  . 1-ta’rif. Agar E to‘plamdagi har bir ) ,... , ( mx x x x 2 1  nuqtaga biror f qoidaga ko‘ra bitta haqiqiy u son mos qo‘yilgan bo‘lsa, E to‘plamda ko‘p o‘zgaruvchili ( m ta o‘zgaruvchili) funksiya berilgan (aniqlangan) deyiladi. Uni u x x x x f m   ) ,..., , ( : 2 1 yoki ) ,..., , ( ) ( mx x x f x f u 2 1   ) , ) ,..., , ( ( R u R x x x x m m    2 1 kabi belgilanadi. Bunda E funksiyaning berilish (aniqlanish) to‘plami, mx x x ,..., , 2 1 lar (erkli o‘zgaruchilar) funksiya argumentlari, u esa mx x x ,..., , 2 1 larning funksiyasi deyiladi. Masalan, f har bir   1021   ),(: ,),...,( xRxM Mxxxx m m  nuqtaga ushbu 2 22 21 2 1 1 m m x x x x x x      ... ) ,..., , ( qoida bilan bitta haqiqiy u sonini mos qo‘ysin. Bu holda mR M  to‘plamda aniqlangan 2 22 21 1 mx x x u      ... funksiya hosil bo‘ladi. Aytaylik , ) ,... , ( mx x x f u 2 1  funksiya ( ko ‘ p hollarda bu funksiyani ) (x f u  kabi yozamiz ) mR E  to ‘ plamda berilgan bo ‘ lsin . E x x x x m   ) ,..., , ( 0 02 01 0 6 nuqtaga mos keluvchi 0u son ) (x f u  funksiyaning 0x nuqtadagi xususiy qiymati deyiladi: ) ( 0 0 x f u  . Berilgan funksiyaning barcha xususiy qiymatlaridan iborat ushbu  E x x f u   :) ( (1) to‘plam ) (x f u  funksiyaning qiymatlari to‘plami deyiladi. Agar (1) to‘plam chegaralangan bo‘lsa, ) ,... , ( ) ( mx x x f x f u 2 1   funksiya E to‘plamda chegaralangan deyiladi. 1mR fazodagi ushbu    R x f R x x x x x f x m m    ) ( , ) ,... , ( : ) ( , 2 1 to‘plam ko‘p o‘zgaruvchili ) ,... , ( mx x x f u 2 1  funksiyaning grafigi deyiladi. Masalan, .)1 ln( 2 2 2 2 y x n y x u      Bu funksiyaning aniqlanish to‘plami tekislikning ushbu 2 2 2 2 1 0 4 0 x y x y           sistemani qanoatlantiradigan nuqtalar to‘plamini ifodalaydi. Umuman olganda, ikki o‘zgaruvchiga bog‘liq bo‘lgan ) , ( y x f u  funksiyaning grafigi 3 R fazoda (biz yashab turgan fazoda) sirtni ifodalaydi. Masalan, ushbu 2 2 y x u   funksiyaning grafigi 3 R fazoda aylanma paraboloidni ifodalaydi. Ko’p o’zgaruvchili funksiyaning aniqlanish sohasi K × E = {( x , y ) : x ∈ K , y ∈ E } to’plamga K va E to’plamlarning Dekart ko’paytmasi deyiladi. Tekislikda x < c ( x > c ) shartni qanoatlantiruvchi nuqtalar to’plami x = c to’g’ri chiziq bilan chegaralngan yuqori (pastgi) yarim tekslik bo’ladi. Xuddi 7 shunday tekislikda y < d ( y > d ) to’plamni tasvirlash mumkin. Farzoda esa x < c ( x > c ) shartni qanoatlantiruvchi nuqtalar to’plami x = c tekislik bilan chegaralangan va bu tekislikni o’ng (chap) tomonida yotuvchi yarim fazo bo’ladi. Tekislikda a < x < b shartni qanoatlantiruvchi nuqtalar to`plami x=a va x= b to`g`ri chiziqlar bilan chegaralangan cheksiz yo`lak bo`ladi. Xuddi shunday tekislikda c < y < d to`plamni tasvirlash mumkin. Quyida ba`zi ikki o`zgaruvchili funksiya grafiklarini ko`rsatamiz. 8 z ( x, y )= ax + by + c z ( x , y ) = √ R 2 − x 2 − y 2 z ( x , y ) = x 2 a 2 + y 2 b 2 z ( x , y ) = √ x 2 a 2 + y 2 b 2 z(x,y) ¿ √ x2 a2− y2 b2 ¿ ¿ Z(x,y) = sin (x+y) 1-misol. u ( x , y ) = √ 1 − x 2 + √ y 2 − 1 funksiyaning aniqlanish sohasini toping. Funksiya aniqlangan bo'lishi uchun ildiz ostidagi ifodalar nomanfiy bo'lishi kerak. 9 Shuning uchun 1 − x 2 = ( 1 − x ) ( 1 + x ) ≥ 0 , y 2 − 1 = ( y − 1 ) ( y + 1 ) ≥ 0 . Shuning uchun u ( x , y ) funksiya x∈[−1;1],y∈¿∪¿ shartni qanoatlantiruvchi nuqtalar to'plamida aniqlangan. Quyidagi chizmada funksiyaning aniqlanish sohasi tasvirlangan. 2-misol. u ( x , y ) = √( x 2 + y 2 − 1 )( 4 − x 2 − y 2 ) funksiyaning aniqlanish sohasini toping. Ildiz ostida turgan ifoda ( x 2 + y 2 − 1 )( 4 − ( x 2 + y 2 )) ≥ 0 bo'lishi kerak. Agar t = x 2 + y 2 bo'lsa u holda ( t − 1 ) ( 4 − t ) ≥ 0 tengsizlikdan 1 2 ≤ t = x 2 + y 2 ≤ 2 2 bo'lishi kelib chiqar ekan. Demak aniqlash sohasi 12≤x2+y2≤22 shartni bajaruvchi o'yilgan doira bo'lar ekan. 3-misol. u(x,y)=arccos x x+y funksiyaning aniqlanish sohasini toping. arccos x x+y funksiya aniqlangan bo'lishi uchun | x x + y | ≤ 1 bo'lishi kerak. Ya'ni ¿ x ∨ ≤ ∨ x + y ∨ ⇔ x 2 ≤ x 2 + 2 xy + y 2 ⇔ y ( 2 x + y ) ≥ 0 . Agar y≥0 bo'lsa u holda y≥−2x , agar y<0 bo'lsa u holda y≤−2x shartni bajaruvchi nuqtalar to'plami bo'ladi. Yani bu funksiyaning aniqlanish sohasi {(x,y):y2+2xy ≥0} yoki quyidagicha ushbu { ( x , y ) : y ≥ 0 , y ≥ − 2 x } ∪ { ( x , y ) : y < 0 , y ≤ − 2 x } ko'rinishda yozish mumkin. 10 4-misol. u=ln (y2− 4x+8) funksiyaning aniqlanish sohasini toping. Funksiyaning aniqlanish sohasi y2− 4x+8>0 shartni bajaruvchi nuqtalar to'plamidan iborat. Ya'ni bu soha y 2 = 4 ( x − 2 ) parabolani chap tomoni bo'ladi. 1.2 R m fazoda ketma-ketlik va uning limiti Ushbu akslantirishning tasvirlaridan tuzilgan to’plam R m fazoda ketma-ketlik deyiladi va 3* kabi belgilanadi. Har bir ni ketma-ketlik hadlari hadlari deyiladi. R m fazoda biror { x (n) }: 11 Ketma-ketlik va a = (a 1 , a 2 , . . . a m ) nuqta berilgan bo’lsin. Ta’rif Agar olinganda ham shunday topilsaki, ixtiyoriy n > n 0 uchun tengsizlik bajarilsa, a nuqta { x (n) } ketma-ketlikning limiti deyiladi va yoki da kabi belgilanadi. Agar { x (n) } ketma-ketlik limitga ega bo’lsa, u yaqinlashuvchi ketma-ketlik deyiladi. 1-misol R m fazoda ushbu ketma-ketlikning limiti a = (0, 0, . . . 0) ekanini ko’rsating. sonni olaylik. Shu ga ko’ra ni topamiz. Unda uchun bo’ladi. Demak, 12 Ta’rifga ko’ra bo’ladi. Teorema R m fazoda ketma-ketlikning a = (a 1 , a 2 , . . . a m ) ni intilishi: uchun bir yo’la . . . . . . . . . bo’lishi zarur va yetarli. Demak, Bu teorema R m fazoda ketma-ketlikning limiti sonli ketma-ketlikning limitiga kelishini ifodalaydi. 1.3 Ko’p o’zgaruvchili funksiya va uning limiti. Faraz qilaylik, ) (x f funksiya m m R E R x   ) ( to`plamda berilgan, mR x 0 nuqta E ning limit nuqtasi bo`lsin. U holda m R fazoda shunday  )(n x : 13 ,.... ,...., , )( )2( )1( n x x xketma-ketlik topiladiki: 1) N n  da 0x x E x n n   )( )( , , 2)  n da 0x x n )( bo`ladi (bunday ketma-ketliklar istalgancha bo`ladi). 2-ta’rif (Geyne). Agar 1) N n  da 0x x E x n n   )( )( , ; 2)  n da 0x x n )( shartlarni qanoatlantiruvchi ixtiyoriy  )(n x ketma-ketlik uchun  n da A x f n ) ( )( bo`lsa, A son f(x)= f(x1,x2,… ,xm) funksiyaning ) ,..., , ( 0 02 01 0 mx x x x  nuqtadagi limiti (karrali limiti) deyiladi. Uni A x f x x   ) ( lim 0 yoki limx1→x10 x2→x20 …xm→xm0 f(x1,x2,… ,xm)= A kabi belgilanadi. Eslatma . Agar     ,....)2,1 , , ( ,....),2,1 , , ( 0 )( )( )( 0 )( )( )(       n x y E y y n x x E x x n n n n n n 14 ketma-ketliklar uchun  n da 0 0 x y x x n n   )( )( , bo`lib, B y f A x f n n   ) ( , ) ( )( )( , BA  bo`lsa, ) (x f funksiya 0x nuqtada limitga ega bo`lmaydi. 3-ta’rif (Koshi). Agar 0  son olinganda ham shunday 0   ) (   topilsaki,     ) , ( 0 0 x x tengsizlikni qanoatlantiruvchi E x   mR E  da   Axf )( tengsizlik bajarilsa, A son ) (x f funksiyaning 0x nuqtadagi limiti (karrali limiti) deyiladi. Bu ta’rifni qisqacha qilib quyidagicha ham aytsa bo`ladi. Agar                  A x f x x U E x ) ( : \) ( , , 0 0 0 0 bo`lsa, A soni ) (x f funksiyaning 0x nuqtadagi limiti deyiladi. Xususiy holda, 2  m bo`lganda 2 R fazodagi (tekislikdagi) biror to`plamda aniqlangan ikki o`zgaruvchiga bog`liq bo`lgan ) , ( y x f u  funksiyaga ega bo`lamiz. 15 uAytaylik, ) , ( y x f funksiya 2R E  to`plamda berilgan bo`lib, 2 0 0 R y x ) , ( nuqta E ning limit nuqtasi bo`lsin. Bu ikki o`zgaruvchili funksiya limiti ta’riflari quyidagicha bo`ladi: Agar 1) N n  da ) , ( ) , ( , ) , ( 0 0 y x y x E y x n n n n   2)  n da ) , ( ) , ( 0 0 y x y x n n  shartni qanoatlantiruvchi ixtiyoriy   ),( nn yx nuqtalar ketma-ketligi uchun  n da A y x f n n ) , ( bo`lsa, A son f(x,y) funksiyaning ) , ( 0 0 y x nuqtadagi limiti (karrali limiti) deyiladi va   Ayxf yxyx   ),(lim 00 ,),( yoki A y x f y y x x   ) , ( lim 00 kabi belgilanadi. Agar 0  olinganda ham shunday 0  topilsaki,       ) , (), , ( 0 0 0 y x y x tengsizlikni qanoatlantiruvchi E y x   ) , ( da    A y x f ) , ( tengsizlik bajarilsa, A son ) , ( y x f funksiyaning ) , ( 0 0 y x nuqtadagi limiti (karrali limiti) deyiladi. 1 -misol. Ushbu 16 2 2 2 2 2 ) ( ) , ( y x y x y x y x f   funksiyaning )0,0( nuqtada limiti mavjud emasligi ko`rsatilsin. ◄ Ravshanki, bu funksiya     0,0 \2R to`plamda aniqlangan va )0,0( nuqta shu to`plamning limit nuqtasi. )0,0( nuqtaga intiluvchi                          n n n n 1 1 1 1 , , , ketma-ketliklarni olaylik:     0011 0011 ,,,,,           nnnn .       n n 1 1, hamda        n n 1 1, nuqtalarda ,....) , , ( 3 2 1n berilgan funksiyaning qiymatlari 14 111 111 2           nnnf nnf ,,, ....), , ( 2 1 n bo`lib , 011 111           nnf nnf ,,, bo`ladi. Funksiya limitining Geyne ta’rifidan foydalanib, berilgan funksiyaning ) , ( ) , ( 0 0  y x da limitga ega emasligini topamiz.► 2-misol. Ushbu 17            бўлса 0 агар, 0 бўлса 0 агар, ) , ( 2 2 2 2 2 2 y x y x y x xy y x ffunksiyaning ) , ( ) , ( 0 0  y x dagi limiti 0 bo`lishi ko`rsatilsin. ◄ Koshi ta’rifidan foydalanib topamiz: 0  son uchun   2  deyilsa,       )0,0(), , ( 0 y x tengsizlikni qanoatlantiruvchi 2 ) , ( R y x   da               2 1 0 0 2 1 2 1 0 2 2 2 2 ) , (), , ( ) , ( y x y x y x xy y x f bo`ladi. Demak, 0 ) , ( lim 00   y x f yx .► 3 0 . Takroriy limitlar. Faraz qilaylik, ) ,... , ( ) ( mx x x f x f 2 1  funksiya mR E  to`plamda berilgan bo`lib, m m Rxxxx  ),...,,( 00 20 10 shu E to`plamning limit nuqtasi bo`lsin. m ta mx x x ,... , 2 1 o`zgaruvchilarga bog`liq bo`lgan ) ,... ( mx x f 1 funksiyada mx x x ,... , 3 2 o`zgaruvchilar tayinlansa, ravshanki, u bitta 1x o`zgaruvchining funksiyasiga aylanadi. Aytaylik, bu funksiya 01 1 x x  da limiga ega bo`lsin : 18 ) ,..., , ( ) ,..., , ( lim 3 2 1 2 1 01 1 m m x x x x x x x x f  . Endi ) ,..., , ( mx x x 3 2 1 funksiyada mx x x ,..., , 4 3 o`zgaruvchilari tayinlanib, so`ng 02 2 x x  limitga o`tilsa ) ,..., , ( ) ,..., , ( lim 4 3 2 3 2 1 02 2 m m x x x x x x x x     bo`lib, berilgan funksiyaning ) ,..., , ( lim lim 2 1 01 1 02 2 m x x x x x x x f   limiti hosil bo`ladi. Xuddi shunga o`xshash ) ,..., , ( mx x x f 2 1 funksiyaning ki i i x x x , , ,  2 1 o`zgaruvchilari mos ravishda 0 0 0 2 1 ki i l x x x ,...., , larga intilgandagi limiti ),...,,(lim...lim 21 0 110 m xxxx xxxf ii ki ki  ni ham qarash mumkin. Odatda, bu limitlar ) ,..., , ( mx x x f 2 1 funksiyaning takroriy limitlari deyiladi. ) ,..., , ( mx x x f 2 1 funksiya argumentlari mx x x ,... , 2 1 lar mos ravishda 0 0 2 0 1 mx x x ,..., , sonlarga turli tartibda intilganda funksiyaning turli takroriy limitlari hosil bo`ladi. 3-misol. Ushbu 19            бўлса 0 агар, 0 бўлса, 0 агар, ) , ( 2 2 2 2 2 2 y x y x y x xy y x ffunksiyaning )0,0( da takroriy limitlari topilsin. ◄Berilgan funksiyaning takroriy limitlarini topamiz: ,0lim),(lim 22 00    yx xy yxf xx ,0 ) , ( lim lim 0 0    y x f x y ,0lim),(lim 22 00    yx xy yxf yy 0 ) , ( lim lim 0 0    y x f y x . Demak, berilgan funksiyaning )0,0( nuqtadagi takroriy limitlari bir-biriga teng bo`lib, ular 0 ga teng.► 4-misol. Ushbu            бўлса 0 3 агар, 0 , бўлса 0 3 агар, 3 2 ) , ( 2 y x y x y x y x y x f funksiyaning )0,0( nuqtadagi takroriy limitlari topilsin. ◄Berilgan funksiyaning takroriy limitlari quyidagicha bo`ladi: , 31 32 lim 0     yx yx x ; 31 32 limlim 00     yx yx xy ,2 3 2 lim 0     y x y x y 2 3 2 lim lim 0 0      y x y x y x . 20 Ayni paytda, berilgan funksiya )0,0( ) , (  y x da limitga (karrali limitga) ega bo`lmaydi, chunki     0045 0011 ,,,,,           nnnn ketma-ketliklar uchun , , 4 1 4 1 1 1        n n f 17 6 17 645      nnf , bo`lib, ular bir-biriga teng emas.► 5-misol. Ushbu         бўлса 0 агар, 0 бўлса, 0 агар,1 sin ) , ( x x x y x y x f funksiyaning )0,0( nuqtadagi takroriy limitlari topilsin. ◄Bu funksiya uchun , ) , ( lim 0 x y x f y   ,0 ) , ( lim lim 0 0    y x f y x bo`lib, ),(limlim 0 0 yxfx y   esa mavjud bo`lmaydi. 21 Ayni paytda, ) , ( ) , ( 0 0  y x da berilgan funksiyaning limiti (karrali limiti) mavjud bo`ladi, chunki )0(1 sin0),(  xyx xyxyxf bo`lib, 0 ) , ( lim 00   y x f yx bo`ladi.► Faraz qilaylik, ) , ( y x f funksiya 2 R fazodagi  b y y a x x R y x E       0 0 2 , : ) , ( to`plamda berilgan bo`lsin. 2-teorema. Agar 1) ) , ( ) , ( 0 0 y x y x  da ) , ( y x f funksiyaning limiti (karrali limiti) mavjud va , ) , ( lim 00 A y x f y y x x   2) har bir tayinlangan x da )(),(lim 0 xyxf yy    (2) mavjud bo`lsa, u holda  y x f yyxx , lim lim 00  takroriy limit mavjud va 22   A y x f y y x x    , lim lim00 bo`ladi. ◄Aytaylik, A y x f y y x x   ) , ( lim 00 bo`lsin. Limit ta’rifiga binoan, 0    olinganda ham shunday 0   topiladiki, ushbu     E y y x x R y x         0 0 2 , : , to`plamning barcha  y x, nuqtalari uchun     A y x f , tengsizlik bajariladi. Keyingi tengsizlikdan, 0y y da limitga o`tib topamiz:       A x . Demak,   A x x x    0 lim . (3) (2) va (3) munosabatlardan   A y x f yyxx   , lim lim 00 bo`lishi kelib chiqadi.► Xud d i shunga o`xshash quyidagi teorema isbotlanadi. 3-teorema. Agar 23 1)    0 0 y x y x , ,  da  y x f , funksiyaning limiti (karrali limiti) mavjud va A y x f y y x x   ) , ( lim 00 , 2) har bir tayinlangan y da    y y x f x x   , lim 0 mavjud bo`lsa, u holda  y x f y y x x , lim lim 0 0   takroriy limit mavjud va   A y x f yyxx   , lim lim 00 bo`ladi. Natija . Agar  y x f , funksiya uchun bir vaqtda yuqoridagi 2,3- teoremalarning shartlari bajarilsa, u holda    y x f y x f y x f x x y y y y x x y y x x , lim lim , lim lim ) , ( lim 0 0 0 0 00        bo`ladi. II bob. Ko’p o’zgaruvchili funksiyalarning uzluksizligi. 2.1 Ko’p o’zgaruvchili funksiyalarning uzluksizligi R m fazodagi M to’plamda funksiya berilgan bo’lib, nuqta shu to’plamning limit nuqtasi bo’lsin. Ta’rif Agar 24 da, ya’ni . . . da funksiyaning limiti mavjud bo’lib, ya’ni bo’lsa, funksiya nuqtada uzluksiz deb ataladi. Ta’rif (Geyne ta’rifi) Agar M to’plamning nuqtalaridan tuzilgan, a ga intiluvchi har qanday { x (n) } ketma-ketlik olinganda ham mos { f(x (n) ) } ketma-ketlik hamma vaqt f(a) ga intilsa, f(x) funksiya a nuqtada uzluksiz deb ataladi. Ta’rif (Koshi ta’rifi) Agar son uchun shunday topilsaki, tengsizlikni qanoatlantiruvchi barcha nuqtalarda tengsizlik bajarilsa, f(x) funksiya a nuqtada uzluksiz deb ataladi. funksiya argumentlarining orttirmalari ga mos ushbu 25 ayirma f(x) funksiyaning a nuqtadagi to’liq orttirmasi deyiladi va kabi belgilanadi: . . . . . . . . . . . ayirmalar 24* funksiyaning a nuqtadagi hususiy orttirmalari deyiladi. Ta’rif Agar bo’lsa, f(x) funksiya a nuqtada uzluksiz deyiladi. Ta’rif Agar f(x) funksiya M to’plamning har bir nuqtasida uzluksiz bo’lsa, funksiya shu to’plamda uzluksiz deyiladi. Shuni ta’kidlash lozimki, yuqorida keltirilgan ta’riflar ko’p o’zgaruchili funksiyaning barcha o’zgaruvchilari bo’yicha uzluksizligini ifodalaydi. 2.2 Uzluksizlik funksiyalarning xossalari Biz quyida ko’p o’zgaruvchili uzluksiz funksiyalarning xossalarini keltiramiz. Bunda bir o’zgaruvchili uzluksiz funksiyalarning xossalari to’g’risidagi ma’lumotlardan to’la foydalana boramiz. Ko’p o’zgaruvchili uzluksiz funksiyalar ham bir o’zgaruvchili uzluksiz funksiyalarning xossalari kabi xossalarga ega. f(x) funksiya to’plamda berilgan bo’lsin, M to’plamdan biror x 0 nuqta olib, bu nuqtaning shu to’plamga tegishli bo’lhan yetarli kichik atrofini qaraylik. f(x) funksiya x 0 nuqtada uzluksiz bo’lsin. Bunday f(x) funksiyaning x 0 nuqtaning yetarli kichik atrofidagi xossalarini (lokal xossalarini) o’rganamiz: 26 1. Agar f(x) funksiya nuqtada uzluksiz bo’lsa, u holda x 0 nuqtaning yetarli kichik atrofida funksiya chegaralangan bo’ladi. Isbot Funksiya uzluksizligi ta’rifiga ko’ra bo’lib, undan f(x) funksiyani x 0 nuqtada chekli limitga ega ekanligi kelib chiqadi. Chekli limitga ega bo’lgan funksiyaning xossalaridan esa, f(x) funksiyani x 0 nuqtaning yetarli kichik atrofida chegaralanganligini topamiz. 2. Agar f(x) funksiyani x 0 nuqtada uzluksiz bo’lib, bo’lsa, x 0 nuqtaning yetarli kichik atrofidagi x nuqtalarda bo’ladi. Isbot f(x) funksiya x 0 nuqtada uzluksizligi ta’rifiga ko’ra, olinganda ham shunday topiladiki, barcha nuqtalar uchun bo’ladi. Bu yerda (agar bo’lsa, ) deb olsak, fikrimizning tasdig’iga ega bo’lamiz. Demak, f(x) funksiya x 0 nuqtada uzluksiz va bo’lsa, x 0 nuqtaning yetarli kichik atrofidagi x nuqtalarda funksiya qiymatlarining ishorasi f(x 0 ) ning ishorasi bilan bir xil bo’lar ekan: 3. Agar f(x) funksiya x 0 nuqtada uzluksiz bo’lsa, x 0 nuqtaning yetarli kichik atrofidagi nuqtalar uchun 27 tengsizlik o’rinli bo’ladi. Isbot f(x) funksiyaning x 0 nuqtada uzluksizligiga asosan olinganda ham, ga ko’ra shunday topiladiki, barcha nuqtalar uchun bo’ladi. Jumladan nuqtalar uchun ham tengsizlik o’rinli bo’ladi. Keyingi tengsizliklardan esa bo’lishi kelib chiqadi. 2.3 . Ko’p o’zgaruvchili funksiyaning tekis uzluksizgi. Kantor teoremasi. f(x) funksiya to'plamda berilgan bo'lsin. Ta'rif. Agar son uchun topilsaki, M to'plamning tengsizlikni qanoatlantiruvchi ixtiyoriy va ( ) nuqtalarida tengsizlik bajarilsa, f ( x ) funksiya M to'plamda tekis uzluksiz funksiya deb ataladi. Funksiyaning tekis uzluksizligi ta'rifidagi son gagina bog'liq bo'ladi. Ravshanki, agar f(x) funksiya to'plamda tekis uzluksiz bo'lsa, u shu to'plamda uzluksiz bo'ladi. Misol. Ushbu 28 funksiyaning to'plamda tekis uzluksiz bo’lishi ko'rsatilsin. sonni olib, unga ko'ra topiladigan sonni deb olsak, u holda tengsizlikni qanoatlantiruvchi18* nuqtalar uchun bo'ladi. Demak, berilgan funksiya to'plamda tekis uzluksiz. Teorema. (Kantor teoremusi). Agar f(x) funksiya chegaralangan yopiq M to'plamda uzluksiz bo'lsa, funksiya shu to'plamda tekis uzluksiz bo'ladi. Isbot. Teskarisini faraz qilaylik, ya'ni f(x) funksiya chegaralangan yopiq M to'plamda uzluksiz bo'lsinu, ammo tekis uzluksizlik ta'rifidagi shart bajarilmasin. Bu holda biror son va ixtiyoriy son uchun M to'plamda tengsizlikni qanoatlantiruvchi shunday va ( ) nuqtalari topiladiki, bo'ladi. Nolga intiluvchi musbat sonlar ketma-ketligi olaylik: 29 (1) Farazimizga ko'ra, yuqoridagi son va ixtiyoriy uchun M to'plamda shunday va nuqtalar topiladiki, va va . . . . . . va bo'ladi. Modomiki, M - chegaralangan to'plam va ekan, unda Boltsano-Veyershtrass teoremasiga ko'ra ketma-ketlikdan yaqinlashuvchi qismiy ketma-ketlik ajratish mumkin: (2) M yopiq to'plam bo'lganligi sababli bo'ladi. Yuqoridagi ketma-ketlikdan ajratilgan qismiy ketma-ketlikning limiti ham a ga teng bo'ladi. Haqiqatdan ham, ushbu tengsizlikdagi lar uchun (1) va (2) munosabatlarga ko'ra da bo'lishini e'tiborga olib, da ekanini topamiz. Shunday qilib, da . 30 Xulosa Men ushbu kurs ishimda to’plamlar, ularning limiti, ko’p o’zgaruvchili funksiyalar va ularning uzluksizligi haqida fikr yuritdim. Sifatli ta‘lim olish uchun ta‘lim vositalarining ahamiyati katta.Xalqimizda ajoyib naql bor ―Ish quroling soz bo‘lsa, mashaqqating oz bo‘lur. Rivojlanib borayotgan texnikalashuv sharoitida, albatta ta‘lim vositalari ham yangilashib borishi tabiiy. Kurs ishida nomlari keltirilgan zamonaviy ta‘lim vositalaridan kelajakda akadamik litsey maktab va oily o‘quv yurtlarida foydalanilsa maqsadga muvofiq bo‘ladi va yaxshi natijalarga erishish mumkin. Ta‘lim maqsadlari, uning mazmuni, o’qitish va ta‘lim berish usullari, nazorat va natijalarni baholashni o’zaro bog’liklikda loyihalash ko’pincha an‘anaviy o’quv jarayonida yetishmaydigan narsadir. Jahon pedagogika fani ilmiy – texnika taraqqiyoti ta‘sirini boshdan kechirib, psixologiya, kibernetika, tizimlar nazariyasi, boshqaruv nazariyasi va boshqa fanlar yutuqlarini birlashtirib, hozirgi davrda faol yangilanish (innovatsiya) jarayonlari bosqichidaturar ekan, inson imkoniyatlarini samarali rivojlantirish amaliyotiga boy mahsul bermoqda. 31 edagogik texnologiya usullari dastlab o’qitishning harakatini namunaviy vaziyatdagi belgilangan qoida bo’yicha o’zlashtirish talab etiladigan mahsuldor darajasi uchun ishlab chiqilgan. Mahsuldor ta‘lim har qanday ta‘limning zaruriy tarkibiy qismi hisoblanib, u insoniyat jamg’argan tajribani aniq o’quv fani doirasida o’zlashtirish bilan bog’liq. 1997-yilda qabul qilingan O‘zbekiston Respublikasining―Ta‘lim to‘g‘risidagi qonuni va ― Kadrlar tayyorlash milliy dasturi milliy ta‘lim taraqqiyoti va milliy kadrlar tayyorlash tizimi istiqbollarini belgilovchi xujjat sifatida bu sohadagi ishlarni rivojlantirishda yana bir tarixiy davr boshlanishiga zamin yaratdi. Kadrlar tayyorlash Milliy dasturi asosiy vazifalaridan biri bu ta‘lim jarayonidagi sifat ko‘rsatkichlarini yaxshilash, ya‘ni jahon andozalariga mos, raqobatbardosh, yuqori saviyaga ega bo‘lgan mutaxassislar tayyorlashdir.Ushbu murakkab muammolarni yechimini topib, ularni amalda keng qo‘llash oliy ta‘lim tizimi xodimlari oldiga juda katta vazifalar belgilaydi. 32 Foydalanilgan adabiyotlar ro’yxati 1. Mirziyayev Sh.M “Milliy taraqqiyot yo’limizni qat’iyat bilan davom ettiramiz” .Toshkent. “O’zbekiston” 2017 2. Azlarov T, Mansurov X. “Matematik analiz asoslari - 1”. Toshkent, “O,qituvchi”, 1989 - yil 3. Azlarov T, Mansurov X. “Matematik analiz assoslari -2”. Toshkent “O’zbekirton”,1995-yil 4. G.Xurdoyberganov, A.K.Vorisova, X.T.Mansurov, B.A. Shoimqulov. Matematik analizdan ma’ruzalar 1-qism.-T.:Voris nashiriyot, 2010-y. 5.Soatov Yo.U. Oliy matematika. 3- qism.-T.:O’qituvchi, 1996. 6. Shoimqulov B.A.Tuychiyev T.T.,Djumaboyev D.X. Matematik analizdan mustaqil ishlar.T. “O’zbekiston faylasuflari milliy jamiyati”.2008. 7. www.edu.uz - O’zbekiston Respublikasi oliy va o’rta maxsus ta’lim vazirligi sayti. 8. www.press-service.uz – O’bekiston Republikasi Prezidentining matbuot xizmati sayti. 9. A.Sadullayev, H. Mansurov, G.H 10. I.Israilov, Z. Pashayev. Matematika. Akademik litsey uchun sinov darslik. Toshkent .”O’qituvchi” 2005 33 11. Umirbekov A.U. Shaabzalov Sh.Sh. Matematikani takrorlang. Toshkent. “O’qituvchi”, 1989 y 34

Ko’p o’zgaruvchili funksiyalar

Kirish……………………………………………………………………………...3 

I BOB. KO’P O’ZGARUVCHILI FUNKSIYALAR

1.1-§. Ko‘p o‘zgaruvchili funksiya tushunchasi …………………........................5

1.2-§. Rm fazoda ketma-ketlik va uning limiti ….................................................10

1.3-§. Ko’p o’zgaruvchili funksiya va uning limiti....………………...................12

II BOB. KO’P O’ZGARUVCHILI FUNKSIYALARNING UZLUKSIZLIGI.

2.1-§ Ko’p o’zgaruvchili funksiyalarning uzluksizligi..........................................23

2.2-§ Uzluksizlik funksiyalarning xossalari...........................................................25

2.3-§ Ko’p o’zgaruvchili funksiyaning tekis uzluksizgi. Kantor teoremasi...........27

Xulosa……………………………………………………………………….........30

Foydalanilgan adabiyotlar………………………………………………………...32

Купить