Lebeg integrali

Информация о документе

Цена	12000UZS
Размер	281.2KB
Покупки	4
Дата загрузки	07 Декабрь 2024
Расширение	docx
Раздел	Курсовые работы
Предмет	Алгебра

Продавец

Yulduzxon

Дата регистрации 07 Декабрь 2024

4 Продаж

Lebeg integrali

Купить

Mundarija.
Kirish. 4
1-§. Jordan va Lebeg o’lchovi………………………….. 6
2-§. To’g’ri chiziq va tekislikda Lebeg ma’nosida o’lchovli
to’plamlar……………………………………………….. 14
3-§. O’lchovli to’plamlarning xossalari………………… 18
4-§. Lebeg ma’nosida o’lchovli to’plamlar uchun
misollar……………………………………………………… 29
Xulosa. 32
Foydalanilgan adabiyotla r. 34
1

“Tanqidiy tahlil, qat’iy tartib-intizom va shaxsiy
javobgarlik- har bir rahbar faoliyatining kundalik
qoidasi bo’lishi kerak.”
Sh.Mirziyoyev.
KIRISH
O`zbekistоnning iqtisоdiy va ijtimоiy sоhalarda yuqоri natijalarga erishishi,
jahоn iqtisоdiy tizimida to`laqоnli sheriklik o`rnini egallay bоrishi, insоn
faоliyatining barcha jabhalarida zamоnaviy axbоrоt texnоlоgiyalaridan yuqоri
darajada fоydalanishning ko`lamlari qanday bo`lishiga hamda bu texnоliyalar
ijtimоiy mehnat samaradоrligining оshishida qanday ahamiyat kasb etishiga
bоg`liq.
Oliy ta’lim tizimini kelgusida yanada takomillashtirish va kompleks
rivojlantirish bo’yicha eng muhim vazifalar quyidagilar etib belgilandi:
Har bir oily ta’lim muassasasi jahonning yetakchi ilmiy-ta’lim massasalari
bilan yaqin hamkorlik aloqalari o’rnatish, o’quv jarayoniga xalqaro ta’lim
standartlariga asoslangan ilg’or pedagogik texnalogoyalar, o’quv dasturlari va
o’quv uslubiy materiallarini keng joriy qilish o’quv-pedagogik faoliyatga, master-
klasslar o’tkazishga, malaka oshirish kurslariga xorijiy hamkor ta’lim
muassasalaridan yuqori malakali o’qituvchilar va olimlarni faol jalb qilish, ularni
bazasida tizimli asosda respublikamiz oily a’lim muassasalari magistrant, yosh
o’qituvchi va ilmiy xodimlarning stajirovka o’tashlarini, professor-o’qituvchilarni
qayta tayyorlash va malakasini oshirishni tashkil qilish. Oliy malumotli
mutaxassislar tayyorlashning maqsadli parametrlarini shakllantirish, oily ta’lim
muassasalarida o’qitish yo’nalishlari va mataxassisliklarini istiqbolda mintaqalar
va iqtisodiyot tarmoqlarini kompleks rivojlantirish, amalga oshrilayotgan hududiy
va tarmoq dasturlarining talablarini inobatga olgan holda optimallashtirish. Ta’lim
jarayonini, oily ta’limning o’quv reja va dasturlarini yangi pedagogik
2

texnologiyalar va o’qitish usullarini keng joriy etish, magistratura ilmiy ta’lim
jarayonini sifat jihatdan yangilash va zamonaviy tashkiliy shakllarni joriy etish
asosida yanada takomillashtirish. O’zbekiston Respublikasi Prezidenti Sh.
Mirziyoyevning 2017-yil 7-fevraldagi “O’zbekiston respublikasini yanada
rivojlantirish bo’yicha Harakatlar strategiyasi to’g’risida”gi farmonida ijtimoiy
soha xususan ta’lim va ilm-fan sohalarini rivojlantirish borasida belgilangan
vazifalar ijrosini ta’minlash hamda sohadagi dolzarb hujjatda ta’lim
muassasalarining moddiy texnik bazasini mustahkamlash yangi ta’lim
muassasalarini qurish, ta’mirlash va apital ta’mirlash barobarida ularni zamonaviy
o’quv va labaratoriya jihozlari, kompyuter texnikasi va o’quv metodik
qo’llanmalar bilan ta’minlash nazarda tutilgan.
Kurs ishi mavzusining dalzarbligi. Ravshanki, “Matematik analiz”
kursining Lebeg ma’nosida o’lchovli to’plamlar mavzusi bu fanning xilma-xil va
qiziqarli amaliy tatbiqlariga ega bo’lgan mavzusidir. So’ngi yillarda oliy ta’lim
tizimida bu fan, ayniqsa, bu bo’limga ajratilgan soat birmuncha kamayib ketganligi
sababli, bu nazariyani atroflicha va chuqur o’rganishning imkoniyati cheklanib
qo’yilyapti. Shu munosabat bilan mazkur kurs ishining mavzusini, ayniqsa,
fintegrallovchi ko’paytuvchini o’rganishga bag’ishlangani bejiz emas. Garchi bu
mavzuga oid yetarli materiallar turli xil adabiyotlarda turli darajada aks etgan
bo’lsada, uni sistemali tarzda bir joyga joylashtirib o’rganishni talab darajasida deb
bo’lmaydi. Yuqoridagilarni hisobga olib, kurs ishi mavzusini dolzarb mavzular
qatoriga kiritish mumkin.
Kurs ishi mavzusining asosiy vazifalari : Oliy ta’lim muassasalarda Lebeg
ma’nosida o’lchovli to’plamlar mavzusidagi darslarni tashkil etishda yangi
pedagogik texnologiyalardan foydalanish.
Kurs ishi mavzusining mazmuni : Mazkur kurs ishi kirish, to’rtta
paragrifdan iborat asosiy qism, xulosa va foydalanilgan adabiyotlar ro’yhatidan
iborat.
3

1-§. Jordan va Lebeg o’lchovi.
Biz bu paragrafda Lebeg va Jordan ma’nosida o‘lchovli to‘plam ta’rifini
beramiz.
Elementar to‘plam o‘lchovi. Aytaylik c b a , , va d lar ixtiyoriy sonlar
bo‘lsin. Tekislikda
bxabxabxabxa <<,<,<, 
va
dycdycdycdyc <<,<,<, 
tengsizliklarning istalgan bir jufti bilan aniqlangan to‘plamlar sistemasi berilgan
bo‘lsin. Bu to‘plamlarni to‘g‘ri to‘rtburchaklar deb ataymiz.
Bizga
, , d y c b x a     tengsizliklar bilan aniqlangan to‘g‘ri
to‘rtburchak berilgan bo‘lsin. Agar dcba <,<
bo‘lsa, u chegaralari o‘ziga
qarashli bo‘lgan to‘g‘ri to‘rtburchakni, agar
b a = va d c< yoki b a < va d c=
bo‘lsa kesmani, agar
d c b a = , = bo‘lsa nuqtani va agar b a > yoki d c> bo‘lsa,
bo‘sh to‘plamni aniqlaydi. Ochiq
d y c b x a < < , < < to‘g‘ri to‘rtburchak c b a , ,
va
d larga bog‘liq ravishda chegarasi o‘ziga qarashli bo‘lmagan to‘g‘ri
to‘rtburchak yoki bo‘sh to‘plam bo‘ladi. Yarim ochiq to‘g‘ri to‘rtburchaklarning
har biri bir, ikki yoki uch tomonsiz to‘rtburchaklarni, ochiq, yarim ochiq
oraliqlarni aniqlaydi.

deb tekislikdagi barcha to‘g‘ri to‘rtburchaklar sistemasini belgilaymiz.
1-lemma. Tekislikdagi barcha to‘g‘ri to‘rtburchaklar sistemasi
 yarim
halqa tashkil qiladi.
Isbot.
c b a , , va d sonlari bilan aniqlanuvchi ochiq to‘g‘ri to‘rtburchak
b a =
bo‘lganda bo‘sh to‘plamni aniqlaydi, demak . Ø   Ikki to‘g‘ri
4

$0 x a a1 b1 bcc1 d d1 1 y P5 P1P2 P3 P4 1.2 – chizma. xy 0 1.1 – chizma P1 P2to‘rtburchakning kesishmasi to‘g‘ri to‘rtburchakdir (1.1-chizmaga qarang), ya’ni  21 ,P P dan  2 1 P P  ekanligi kelib chiqadi. Faraz qilaylik abcdP P = to‘g‘ri to‘rtburchak 1111 =1 dcbaP P to‘g‘ri to‘rtburchakni o‘zida saqlasin. U holda d d c c b b a a       1111 , munosabatlar o‘rinli. 1 \P P ayirmani quyidagicha tasvirlash mumkin. , = 54321 P P P P P\ P    bu yerda (1. 2 -chizmaga qarang) P2= Paa1cd , P3= Pa1bd1d, P4= Pb1bcd 1, P5= Pa1b1cc1. Demak, tekislikdagi barcha to‘g‘ri to‘rtburchaklar sistemasi B yarim halqa tashkil qilar ekan.  1-ta’rif.  yarim halqadan olingan va dc b a ,, , sonlari bilan aniqlangan (yopiq, ochiq yoki yarim ochiq) abcdP P = to‘g‘ri to‘rtburchak uchun 5$

y
x0 Q1 Q2
Q3
Q4
1.4-chizma.y
x0 P5
P1 P2
P3 P4
P6
1.3-chizma.) )( ( =) ( c d a b P m   sonni mos qo‘yamiz, agar P bo‘sh to‘plam bo‘lsa 0=)( Pm
deymiz va
R B m  : to‘plam funksiyasini o‘lchov deymiz.
Shunday qilib,
 dagi har bir P to‘g‘ri to‘rtburchakka uning o‘lchovi -
) )( ( =) ( c d a b P m  
son mos qo‘yildi. Bu moslik quyidagi shartlarni
qanoatlantiradi:
1)
) (P m - manfiy bo‘lmagan haqiqiy son.
2)
R m  : o‘lchov additiv, ya’ni agar
kiPPPP
kikn
k  ,=,=
=1 

bo‘lsa, u holda quyidagi tenglik o‘rinli )(=)(
1= kn
k PmPm

ettirishdan iborat.
) ( 
bilan  yarim halqa ustiga qurilgan minimal halqani belgilaymiz.
6

2-ta’rif. ) (  halqa elementlari elementar to‘plamlar deyiladi.
3-teoremaga ko‘ra ixtiyoriy
) (  A to‘plam chekli sondagi o‘zaro
kesishmaydigan to‘g‘ri to‘rtburchaklarning yig‘indisi shaklida ifodalanadi va
aksincha.
1-xossaga ko‘ra quyidagi tasdiq o‘rinli.
1-lemma. Ikki elementar to‘plamning birlashmasi, kesishmasi, ayirmasi va
simmetrik ayirmasi yana elementar to‘plam bo‘ladi.
Endi
) (  halqadagi to‘plamlarning, ya’ni elementar to‘plamlarning
o‘lchovi tushunchasini kiritamiz.
3-ta’rif. Har bir
) ( =
1=
  k
n
k
P A  elementar to‘plamga
 k
n
k
P m A m  
1=
=) (
sonni mos qo‘yuvchi
R m     ) ( : moslikni aniqlaymiz. ) (A m miqdorni A
to‘plamning o‘lchovi deb ataymiz.
Elementar to‘plamlar sistemasi
) (  da aniqlangan m funksiyaning qiymati A
elementar to‘plamni chekli sondagi to‘g‘ri to‘rtburchaklar yig‘indisiga yoyish
usulidan bog‘liq emasligini ko‘rsatamiz. Aytaylik,
  m k P k , 1,2,= , 
va
  n j Q j , 1,2,= , 
larning har biri o‘zaro kesishmaydigan to‘g‘ri to‘rtburchaklar
sistemalari bo‘lib,
j
n
j k
m
k
Q P A   1= 1=
= =
7

 
)(1.=)(
1= AAmAm
kn
k 
tenglik o‘rinli bo‘lsin (1.3 va 1.4-chizma). U holda ikkita kP va j Q to‘g‘ri
to‘rtburchaklarning kesishmasi
j k Q P  to‘g‘ri to‘rtburchak ekanligidan A to‘plam
o‘zaro kesishmaydigan
j k Q P  to‘g‘ri to‘rtburchaklar yig‘indisi shaklida, ya’ni
)(=
1=1= jkn
jm
k QPA

ko‘rinishda tasvirlanadi va
   , = =) (
1=1=1= jkn
jm
kkm
k Q P m P m A m     
   
jkm
kn
jjn
j Q P m Q m A m      1=1=1= = =) (
tengliklar o‘rinli. Oxirgi tengliklar ko‘rsatadiki,
A elementar to‘plamning o‘lchovi
) (A m
uning to‘g‘ri to‘rtburchaklar yig‘indisi shaklida tasvirlanish usulidan
bog‘liq emas ekan, ya’ni elementar to‘plam o‘lchovi
m ning aniqlanishi kerak
ekan.
1. Agar
) (  A to‘plam to‘g‘ri to‘rtburchak bo‘lsa, u holda ) ( =) ( A m A m
bo‘ladi.
2. Agar
) (  A to‘plam chekli sondagi o‘zaro kesishmaydigan ,
1A
,2A
nA, 
elementar to‘plamlarning yig‘indisi shaklida tasvirlansa, ya’ni k
n
k
A A 1=
= u
holda
8

   
(1.1)
n
n AmAm 


xy
0 a
bcd
A A
1.6 – chizma xy
0 a
bcd
AA
1/n
1.5 – chizma tenglik o‘rinli. Haqiqatan ham, ) (   k A
bo‘lganligi uchun
, =
1= kj
km
j k P A  bu yerda
 kjP
- o‘zaro kesishmaydigan to‘g‘ri to‘rtburchaklar sistemasi. U holda
   . = =) ( =
1= 1= 1= 1=1= k
n
k kj
km
j
n
k kj
km
j
n
k
A m P m A m P A      va  
(6.A) tenglik
m o‘lchovning additivlik xossasini ifodalaydi.
1-teorema. Agar
) (  A va   nA elementar to‘plamlarning chekli yoki
sanoqli sistemasi bo‘lib, n
n AA
 
bo‘lsa,
tengsizlik o‘rinli bo‘ladi.
Isbot. Ixtiyoriy
0 >  va A elementar to‘plam uchun
 
2
) (      A m A m
tengsizlikni qanoatlantiruvchi va
A to‘plamda saqlanuvchi yopiq A elementar
to‘plam mavjud (1.5- chizmaga qarang,
n>4(b−a+d−c)
ε ).
9

Har bir elementar nA to‘plam uchun ochiq n n A A  ~ elementar to‘plam
mavjudki (1.6- chizmaga qarang)
   
1
2~


nnn AmAm 
tengsizlik bajariladi.
A va n A~
to‘plamlarning tanlanishiga ko‘ra
n
n AA ~


munosabat o‘rinli bo‘ladi.
Ochiq to‘plamlar sistemasi
 nA~ dan Geyne-Borel lemmasiga ko‘ra
A ni
qoplovchi chekli sondagi
sn n n A A A ~, , ~, ~
2 1  to‘plamlarni ajratish mumkin. A to‘plam
chekli sondagi to‘g‘ri to‘rtburchaklar bilan qoplangani uchun
¿ s m
'
(
~
A ni)¿
tengsizlik o‘rinli. Yuqoridagilardan
¿ ∞ m
'
(
~
A n ) + ¿
       



 

n
nn
nn
n AmAm
=11
=1=1 =
222
ni hosil qilamiz va
0 >  ning ixtiyoriyligidan teoremaning isboti kelib chiqadi. 
1-teorema tasdig‘idagi
m o‘lchovning xossasi, ya’ni A elementar
to‘plamning o‘lchovi uni qoplovchi chekli yoki sanoqli sondagi elementar
10

to‘plamlarning o‘lchovlari yig‘indisidan oshmasligi, m o‘lchovning yarim
additivlik xossasi deyiladi.
m
o‘lchovning yarim additivlik xossasidan uning  - additivlik xossasi
kelib chiqadi, ya’ni quyidagi teorema o‘rinli.
2-teorema.
A elementar to‘plam sanoqli sondagi o‘zaro kesishmaydigan
  , , , , 2 1 nA A A
elementar to‘plamlarning yig‘indisidan iborat, ya’ni
n n
A A 

1=
=
bo‘lsin. U holda
 
n
n A m A m    
=1 =) (
bo‘ladi.
Isbot.
m o‘lchovning chekli additivlik xossasiga ko‘ra
 . = ) (
=1 =1 n
N
n n
N
n
A m A m A m  

 

    
Agar
  N da limitga o‘tsak,
 n n
A m A m    

=1
) (
bo‘ladi. 1.1 - teoremaga ko‘ra
 . ) (
=1 n
n A m A m     
Demak,
 

 
.=)(
=1 n
n AmAm
11

 
(1.2)=)(*
k
kPA PmA
k k 
inf

 
(1.3)).(=)(
1=*
AmPmA
kn
k 

2-§. To’g’ri chiziq va tekislikda Lebeg ma’nosida o’lchovli to’plamlar.
Geometriya va klassik analizda uchraydigan to‘plamlar faqatgina elementar
to‘plamlardan iborat bo‘lmaydi. Shu sababli o‘lchov tushunchasini, uning
xossalarini saqlagan holda elementar to‘plamlar sistemasi ) (  dan kengroq
to‘plamlar sistemasi uchun aniqlashga harakat qilamiz.
Lebeg o‘lchovi nazariyasini bayon qilish jarayonida bizga nafaqat chekli,
balki cheksiz sondagi to‘g‘ri to‘rtburchaklar birlashmalarini ham qarashga to‘g‘ri
keladi. Bunda birdaniga «cheksiz o‘lchov» li to‘plamlarga duch kelmaslik uchun,
dastlab
1} 0 1, 0:) ; {(=     y x y x E birlik kvadratda saqlanuvchi to‘plamlar
bilan chegaralanamiz.
4-ta’rif. Ixtiyoriy
E A  to‘plam uchun
son
A to‘plamning tashqi o‘lchovi deb ataladi. Bu yerda aniq quyi chegara A
to‘plamni qoplovchi to‘g‘ri to‘rtburchaklarning barcha chekli yoki sanoqli
sistemalari bo‘yicha olinadi.
1-eslatma. Agar
A elementar to‘plam bo‘lsa, u holda ). ( =) (* A m A  
Haqiqatan ham,
A elementar to‘plam n P P P , , ,21 
to‘g‘ri to‘rtburchaklarning
birlashmasi ko‘rinishida tasvirlansin, u holda
12

(1.4)).(=)()( *
AQmAm
j
j 

inf}{kPto‘g‘ri to‘rtburchaklar sistemasi A to‘plamni qoplaydi, shuning uchun (1.3)
o‘rinli.
Ikkinchi tomondan,
 j Q sistema A to‘plamni qoplovchi chekli yoki sanoqli
sondagi ixtiyoriy to‘g‘ri to‘rtburchaklar sistemasi bo‘lsa, 1-teoremaga ko‘ra
 j j
Q m A m    ) (
kelib chiqadi. Shuning uchun
Demak, (1.3) va (1.4) lardan
) ( =) ( * A A m   tenglikka ega bo‘lamiz. Shunday qilib,
) ( 
da m va * o‘lchovlar ustma-ust tushar ekan. 
3-teorema. Agar chekli yoki sanoqli sondagi
} { nA to‘plamlar sistemasi uchun
n n
A A  
bo‘lsa, u holda
 
n
n A A **) (    
tengsizlik o‘rinli. Xususiy holda, agar
B A  bo‘lsa, ) ( ) ( * * B A    bo‘ladi.
Isbot. Ixtiyoriy
0 >  va har bir nA uchun tashqi o‘lchov ta’rifiga ko‘ra to‘g‘ri
to‘rtburchaklarning shunday chekli yoki sanoqli
  nk P
sistemasi topiladiki,
   
.
2*
nnn k
kn k
kn APmPA   
va

U holda
13

 
(1.5).=)(
=1*
1 kn
k
PA PmAj
kn
k 
inf
              n n n k k n n k k n A P m A P A * * ) ( va  tengsizlik o‘rinli.
0 >  sonning ixtiyoriyligidan teoremaning isboti kelib chiqadi.

Ma’lumki, elementar to‘plamlar sistemasi
) (  da m va * lar ustma-ust
tushadi. Demak, 1.1-teorema 1.3-teoremaning xususiy holini ifodalaydi.
5-ta’rif. Bizga
E A  to‘plam berilgan bo‘lsin. Agar ixtiyoriy 0 >  uchun
shunday
E B  elementar to‘plam mavjud bo‘lib,   <) (* B A tengsizlik
bajarilsa, u holda
A Lebeg ma’nosida o‘lchovli to‘plam deyiladi. Agar A Lebeg
ma’nosida o‘lchovli to‘plam bo‘lsa, uning o‘lchovi deb tashqi o‘lchovini qabul
qilamiz.
Faqat o‘lchovli to‘plamlar sistemasida aniqlangan
* to‘plam funksiyasi Lebeg
o‘lchovi deb ataladi va u
 bilan belgilanadi.
Shunday qilib, o‘lchovli to‘plamlar sistemasi
 va unda Lebeg o‘lchovi 
aniqlandi. Demak, ixtiyoriy
 A uchun ). ( =) ( * A A  
Bizning asosiy maqsadimiz o‘lchovli to‘plamlar sistemasi
 ni chekli yoki sanoqli
sondagi to‘plamlarning birlashmasi va kesishmasiga nisbatan yopiqligini
ko‘rsatish, ya’ni
 ning  - algebra tashkil qilishini isbotlashdan iborat.
2-eslatma. Agar (6.2) tenglikda aniq quyi chegara
A to‘plamni qoplovchi to‘g‘ri
to‘rtburchaklarning barcha chekli sistemalari bo‘yicha olinsa,
A to‘plamning
Jordan ma’nosidagi tashqi o‘lchovi hosil bo‘ladi, u
) (* A j bilan belgilanadi, ya’ni
14

$Ushbu ) \ ( 1=) ( * * A E j A j  son A to‘plamning Jordan ma’nosidagi ichki o‘lchovi deyiladi. Agar ) ( =) ( * * A j A j bo‘lsa, u holda A Jordan ma’nosida o‘lchovli to‘plam deyiladi. Shuni ta’kidlash joizki, agar A Jordan ma’nosida o‘lchovli to‘plam bo‘lsa, u Lebeg ma’nosida ham o‘lchovli to‘plam bo‘ladi va bu o‘lchovlar o‘zaro teng bo‘ladi. 15$ $3-§. O’lchovli to’plamlarning xossalari. 4-teorema. O‘lchovli to‘plamning to‘ldiruvchisi o‘lchovlidir. Isbot. Teoremaning tasdig‘i elementar to‘plamning to‘ldiruvchisi elementar to‘plam ekanligidan va    B\ E A\ E B A   = tenglikdan kelib chiqadi.  5-teorema. O‘lchovli to‘plamlar sistemasi  halqa tashkil qiladi. Isbot. Teoremani isbotlash uchun o‘lchovli to‘plamlarning kesishmasi va simmetrik ayirmasi yana o‘lchovli to‘plam ekanligini ko‘rsatish yetarli. 2 1,A A o‘lchovli to‘plamlar bo‘lsin. Ta’rifga ko‘ra, ixtiyoriy 0 >  son uchun shunday ) ( 1   B va ) ( 2   B elementar to‘plamlar mavjud bo‘lib, quyidagi tengsizliklar bajariladi     . 2 < , 2 < 2 2 * 1 1 *     B A B A   U holda         22112121 B A B A B B A A        munosabatdan va tashqi o‘lchovning yarim additivlik xossasidan               < 2 2 * 1 1 * 2 1 2 1 * B A B A B B A A        16$

ga ega bo‘lamiz. 21B B 
ning elementar to‘plam ekanligidan 21 A A 
ning
o‘lchovli to‘plam ekanligi kelib chiqadi.
Ikki to‘plam simmetrik ayirmasining o‘lchovli ekanligi
       
22112121 = B A B A B B A A      
tenglikdan kelib chiqadi.

Agar o‘lchovli to‘plamlar sistemasi
 da birlik element mavjud bo‘lsa, u
algebra tashkil qiladi.
 da 1} 0 1, 0:) , {(=     y x y x E to‘plam birlik
element shartlarini qanoatlantiradi. Demak, o‘lchovli to‘plamlar sistemasi

algebra tashkil qilar ekan.
1-natija. O‘lchovli to‘plamlarning birlashmasi va ayirmasi yana o‘lchovli
to‘plamdir.
2-natija. Chekli sondagi o‘lchovli to‘plamlarning birlashmasi va kesishmasi yana
o‘lchovli to‘plamdir.
6-teorema (O‘lchovning additivlik xossasi). Agar
nA A A , , , 2 1  lar o‘zaro
kesishmaydigan o‘lchovli to‘plamlar bo‘lsa, u holda
 k
n
k k
n
k
A A    

 


=1 =1
= 
tenglik o‘rinli.
Teoremani isbotlashda quyidagi lemmadan foydalaniladi.
2-lemma. Ixtiyoriy ikkita
A va B to‘plamlar uchun
)()()( ***
BABA 
  
tengsizlik o‘rinli.
17

Isbot. ) ( B A B A    bo‘lgani uchun 1.3-teoremaga ko‘ra
). ( ) ( ) ( * * * B A B A      
Bu yerdan
) ( ) ( * * B A    hol uchun lemmaning isboti kelib chiqadi. Xuddi
shunday,
) ( B A A B    munosabatdan
) ( ) ( ) ( * * * B A A B      
ni olamiz. Yuqoridagilardan
    ). ( |) ( ) ( | * * * B A B A   
1-teoremaning isboti. Teoremani
2 =n uchun isbotlash yetarli. Bizga 1A va 2A
o‘zaro kesishmaydigan o‘lchovli to‘plamlar berilgan bo‘lsin. Ixtiyoriy
0 >  son
uchun shunday
1B va 2B elementar to‘plamlar mavjudki,
    <) ( , <) ( 2 2 * 1 1 * B A B A  
tengsizliklar bajariladi. 21
= A A A 
va 21 = B B B 
deymiz. 6.1-natijaga ko‘ra
A
to‘plam - o‘lchovli. 1A va 2A to‘plamlar o‘zaro kesishmaganligi uchun
   
221121 B A B A B B     
munosabat o‘rinli va bundan
  2 21   B B m 
tengsizlik kelib chiqadi.
2-lemmaga ko‘ra
, |<) ( ) ( |=|) ( ) ( | 1 1 * 1 * 1 *     B m A A B   
. |<) ( ) ( |=|) ( ) ( | 2 2 * 2 * 2 *     B m A A B   
Endi
m o‘lchovning additivlik xossasiga ko‘ra
18

$. 4 ) ( ) ( ) ( ) ( ) ( =) ( 2 * 1 * 2 1 2 1             A A B B m B m B m B m Agar     2211 B A B A B A      munosabatni hisobga olsak,           6 2 ) ( ) ( ) ( ) ( 2 * 1 * * *           A A B m B A B m A ga ega bo‘lamiz. 0 >  sonning ixtiyoriyligidan    2 * 1 * * ) ( A A A      ni hosil qilamiz. Teskari tengsizlik    2 * 1 * * ) ( A A A      esa 21 A A A   munosabatdan hamda 3-teoremadan kelib chiqadi. Demak,    2 * 1 * * =) ( A A A     tenglik o‘rinli. 2 1,A A va A to‘plamlar o‘lchovli bo‘lganligi uchun * ni  bilan almashtirish mumkin.  3-natija. Ixtiyoriy E A  o‘lchovli to‘plam uchun   ) ( 1= \ A A E    tenglik o‘rinli. Isbot. A va A E \ to‘plamlar o‘zaro kesishmaydi va 1.=)(=)\()( EAEA     Bu yerdan   ). ( 1 =) ( A A E   \ 19$ $  (1.6) 2< 0>   ' n nn A7-teorema. Sanoqli sondagi o‘lchovli to‘plamlarning birlashmasi va kesishmasi yana o‘lchovli to‘plamdir. Isbot.    , , , , 21 n A A A o‘lchovli to‘plamlarning sanoqli sistemasi bo‘lib, n n A A   1= = bo‘lsin. Quyidagi belgilashlarni kiritamiz 2. , \ = , = 1 1=11   n A A A A A kn kn' n'  Ravshanki, ' n n AA   1== hamda 'nA to‘plamlar juft-jufti bilan o‘zaro kesishmaydi. 1 va 2-natijalarga ko‘ra, 'nA to‘plamlar - o‘lchovli. 6-teoremadan hamda tashqi o‘lchovning yarim additivlik xossasidan ixtiyoriy chekli N n uchun quyidagiga ega bo‘lamiz ). ( ) ( = * =1 =1 A A A 'k n k 'k n k             Shuning uchun  'n n A    =1 qator yaqinlashadi. Demak, ixtiyoriy 0 >  son uchun shunday 0n mavjudki, 20$ $  (1.7) 2<*   BC tengsizlik bajariladi. 'n n n A C  0 1= = to‘plam o‘lchovli to‘plamlarning chekli yig‘indisi sifatida o‘lchovli bo‘lgani uchun, shunday B elementar to‘plam mavjudki, tengsizlik bajariladi. U holda          'n nn A B C B A   0> ) ( munosabatdan va o‘lchovning yarim additivlik xossasidan hamda (1.6) va (1.7) lardan foydalansak,         = 2 2 < ) ( 0> *            'n nn A B C B A  kelib chiqadi. Demak, A o‘lchovli to‘plam ekan. O‘lchovli to‘plamlarning to‘ldiruvchisi o‘lchovli ekanligidan hamda  n n n n A E E A \ \   = tenglikdan sanoqli sondagi o‘lchovli to‘plamlarning kesishmasi yana o‘lchovli ekanligi kelib chiqadi.  4-natija. O‘lchovli to‘plamlar sistemasi ,    algebra tashkil qiladi. Natijaning isboti 6.7-teoremadan hamda  sistemada 1} 0 1, 0:) , {(=     y x y x E ning birlik element ekanligidan kelib chiqadi. 8-teoroema (O‘lchovning  - additivlik xossasi). Agar  nA - o‘zaro kesishmaydigan o‘lchovli to‘plamlar ketma-ketligi uchun 21$

 
(1.8)=)(
1= n
n AA 
 
 
(1.9))(
1= AA
n
n  
 
 
(1.10).)(
1= n
n AA 
 
n
n AA
 
1==
bo‘lsa, u holda
tenglik o‘rinli.
Isbot. Ixtiyoriy k da
. 1=A A nk
n  
6 va.3-teoremalarga ko‘ra
  ). ( =
=1 =1
A A A n
k
n n
k
n
    

 

  
Agar
  k da limitga o‘tsak,
tengsizlikka ega bo‘lamiz. O‘lchovning yarim additivlik xossasiga ko‘ra,
(1.9) va (1.10) dan (1.8) tenglik kelib chiqadi.

Yuqorida keltirilgan teorema o‘lchovning sanoqli additivlik yoki
 -
additivlik xossasi deb ataladi. O‘lchovning
 - additivlik xossasidan uning
uzluksizlik xossasi kelib chiqadi.
9-teorema. (O‘lchovning uzluksizlik xossasi). Agar o‘lchovli to‘plamlarning
     
n A A A21
ketma-ketligi uchun
22

$  (1.11),=)( 1 =11   nn n AAA \   (1.12).=)( 1 =   nn NnN AAA \ n n AA   1== bo‘lsa, u holda ).( lim=)( n n AA   Isbot. Ø = A to‘plam bo‘lgan holni qarash yetarli, chunki umumiy hol nA ni A A n \ bilan almashtirish natijasida Ø = A holga keltiriladi. Quyidagi           4332211 = A A A A A A A \ \ \ va           32211 =  NNNNNNN A A A A A A A \ \ \ tengliklar o‘rinli va qo‘shiluvchi to‘plamlar juft-jufti bilan o‘zaro kesishmaydi. O‘lchovning  - additivlik xossasiga ko‘ra (1.11) qator yaqinlashuvchi bo‘lgani uchun uning qoldig‘i (1.12)   N da nolga intiladi. Shunday qilib,   0.=)( lim N N A  5-natija. Agar       n A A A21 o‘lchovli to‘plamlar ketma-ketligi uchun n n AA   1== bo‘lsa, u holda ).( lim=)( n n AA    23$

(1.13))(=)(
, m
nZnm AA 

Natijani isbotlash uchun nA to‘plamlardan ularning to‘ldiruvchilariga o‘tish va 9-
teoremadan foydalanish yetarli.
Ayrim to‘ldirishlar. Biz yuqorida faqat birlik kvadrat
1} 0 1, 0:) , {(=     y x y x E
da saqlanuvchi to‘plamlarni qaradik. Bu
cheklashdan xalos bo‘lish mumkin. Ma’lumki, koordinatalar tekisligini
1} < 1, < :) , {(=     n y n m x m y x E
mn
(
n m , butun sonlar) kvadratlar yig‘indisi ko‘rinishida tasvirlash mumkin:
mn
Znm ER

,2
=
4-ta’rif. Agar istalgan
n m, butun sonlar uchun mnmn E A A  =
to‘plamlar o‘lchovli
bo‘lsa, u holda
A to‘plam o‘lchovli deyiladi. Agar A to‘plam o‘lchovli bo‘lsa,
qator yig‘indisi
A to‘plamning Lebeg o‘lchovi deyiladi.
Agar (1.13) qator yig‘indisi chekli bo‘lsa,
A chekli o‘lchovli to‘plam
deyiladi. Aks holda
A cheksiz o‘lchovli to‘plam deyiladi. Shuning uchun 
o‘lchov cheksiz qiymat ham qabul qilishi mumkin. O‘lchov va o‘lchovli
to‘plamlarning yuqorida o‘rnatilgan barcha xossalari bu hol uchun ham o‘rinli
bo‘ladi. Biroq 9-teoremada (1.11) qator yaqinlashuvchi bo‘lishi uchun
 <) ( 1A 
shartni qo‘shishimiz kerak bo‘ladi. Takidlash lozimki, sanoqlita chekli o‘lchovli
to‘plamlar yig‘indisi cheksiz o‘lchovga ega bo‘lishi mumkin. Tekislikdagi barcha
o‘lchovli to‘plamlar sinfini
 simvol bilan belgilaymiz.
Bu paragrafda tekislikdagi to‘plamlar uchun Lebeg o‘lchovining qurilish
usulini bayon qildik. Sonlar o‘qi
R dagi va uch o‘lchamli 3
R
fazodagi to‘plamlar
24

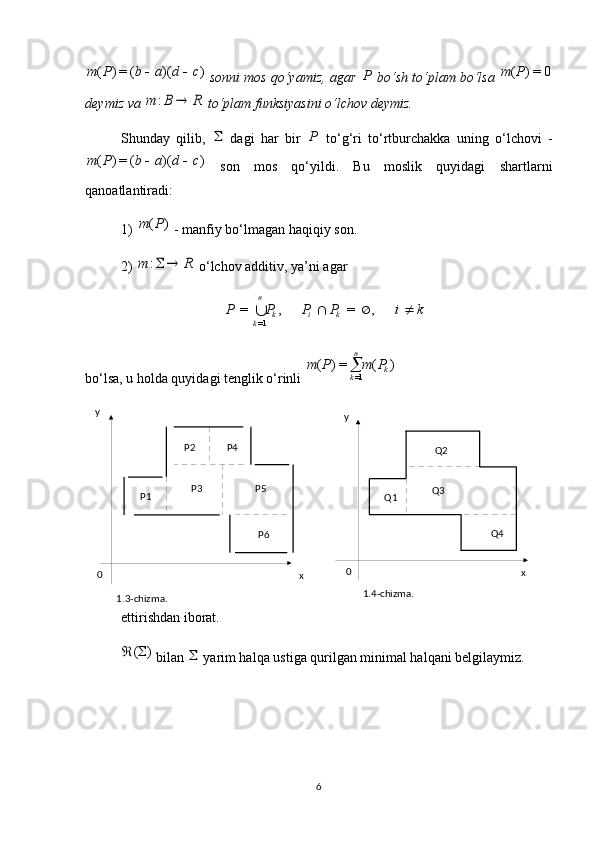
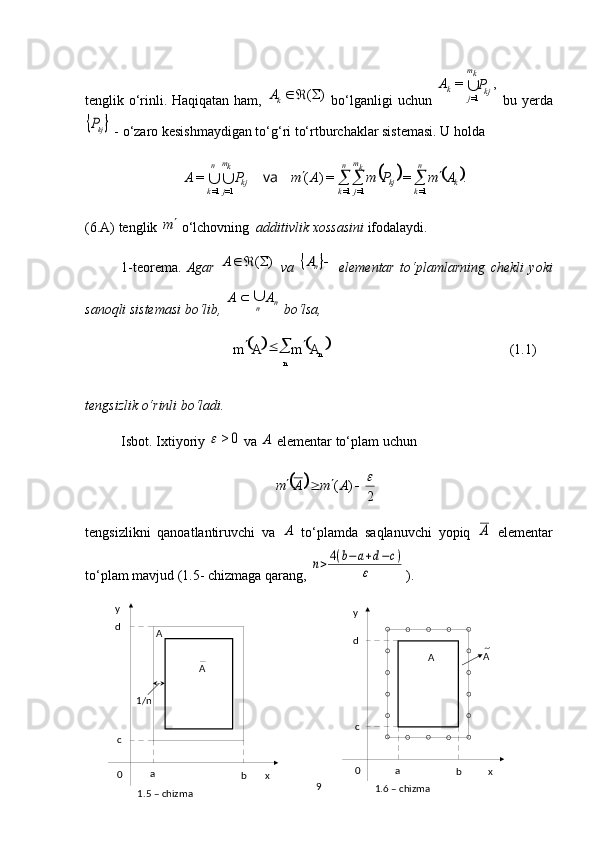
uchun ham Lebeg o‘lchovi shunga o‘xshash usulda quriladi. Masalan sonlar o‘qida
ol’chov dastlab ) , ( b a intervallar, ] , [ b a kesmalar va ), , [ b a ] , ( b a yarim
intervallardan tashkil bo‘lgan
 yarim halqada, ularning uzunligi sifatida
aniqlanib, keyin
 ni saqlovchi minimal halqaga davom ettiriladi. Undan keyin esa
tekislikdagiga o‘xshash usulda Lebeg ma’nosida o‘lchovli to‘plamlardan iborat

algebragacha davom ettiriladi. Aynan shunga o‘xshash usulda Lebeg o‘lchovini
istalgan
n o‘lchamli Evklid fazosida ham qurish mumkin. Tekislikda Lebeg
ma’nosida o‘lchovli to‘plamlarni kiritish jarayonida odatdagi yuza ta’rifidan kelib
chiqdik. Shunga o‘xshash bir o‘lchovli holda Lebeg o‘lchovining kiritilishi interval
(kesma, yarim interval) uzunligi tushunchasiga asoslanadi.
Ayrim umumlashtirishlar. Umuman olganda o‘lchov tushunchasini
boshqacha usulda, ya’ni umumiyroq usulda kiritish mumkin. Bu umumiyroq usulni
sonlar o‘qidagi to‘plamlar uchun amalga oshiramiz.
Bizga sonlar o‘qida aniqlangan kamaymaydigan o‘ngdan uzluksis F
funksiya berilgan bo‘lsin. Interval, kesma va yarim intervallarda F
funksiya
yordamida quyidagi sonlarni mos qo‘yamiz:
),(0)(=),( aFbFbam 

0), ( ) ( =] , [   a F b F b a m
),()(=],( aFbFbam 

0). ( 0) ( =) , [    a F b F b a m
Ravshanki, bu usulda aniqlangan
m interval (kesma va yarim interval) funksiyasi
manfiymas va additiv. Yarim halqada kiritilgan bu o‘lchovga yuqoridagidek
mulohazalarni qo‘llab, qandaydir
)( F 
o‘lchovni qurishimiz mumkin. Bunda F 
o‘lchovga nisbatan o‘lchovli bo‘lgan to‘plamlarning
F  sistemasi sanoqli yig‘indi
va sanoqli keshishmaga nisbatan yopiq bo‘ladi, F

o‘lchov esa  
additiv
bo‘ladi. Umuman olganda, F

o‘lchovga nisbatan o‘lchovli to‘plamlar sinfi F
funksiyaning tanlanishiga bog‘liq. Ammo
R da o‘ngdan uzluksis, kamaymaydigan
istalgan F
funksiya uchun ochiq va yopiq to‘plamlar, shuningdek, ularning
25

$istalgan sanoqli yig‘indi va sanoqli kesishmalari o‘lchovli to‘plamlar bo‘ladi. U yoki bu kamaymaydigan o‘ngdan uzluksiz F funksiyalar vositasida olingan F o‘lchovlar Lebeg-Stiltes o‘lchovlari deb ataladi. Bizga Lebeg o‘lchovi  va Lebeg-Stiltes o‘lchovi F  berilgan bo‘lsin. 5-ta’rif. Agar 0 =) (A  ekanligidan 0 =) (A F  kelib chiqsa, F  absolyut uzluksiz o‘lchov deyiladi. Agar F  o‘lchov chekli yoki sanoqli qiymat qabul qiluvchi F funksiya yordamida aniqlansa, F  diskret o‘lchov deb ataladi. Agar F  o‘lchovda istalgan bir nuqtali to‘plam 0 o‘lchovga ega bo‘lsa va Lebeg o‘lchovi nolga teng bo‘lgan biror A to‘plam uchun 0 =) \ ( A R F  bo‘lsa, u holda F  singulyar o‘lchov deyiladi. Ko‘rsatish mumkinki, istalgan o‘lchov absolyut uzluksiz, diskret va singulyar uzluksiz o‘lchovlar yig‘indisi ko‘rinishida tasvirlanadi va bu tasvir yagonadir. 26$

4-§. Lebeg ma’nosida o’lchovli to’plamlar uchun misollar.
To’plamlar o’lchov topishda asosan, Lebeg bo’yicha aniqlaymiz . Har doim Jordan
bo’yicha to’plamlar o’lchovini aniqlab bo’lmaydi.shuning uchun asosan Lebeg
ma’nosida aniqlanadi.Bunga doir bir qator misollar keltiramiz . Hozir biz Lebeg
ma’nosida o‘lchovli, ammo Jordan ma’nosida o‘lchovli bo‘lmagan to‘plamga
misol keltiramiz.
1-misol.
A = [− 4 ;6 ] Q = Q [− 4;6]
B = [0 ;10 ]/Q = I (0 ;10 ) μ ( A /B )= ?
To’plamning o’lchovini topish uchun avvalo berilgan to’plamlarning ayirmasini
topamiz:

A / B = Q [− 4 ,; 6 ]/ I (0 ;10 )= Q [− 4 ;6 ]
27

$To’plamlar ayirmasi Q [−4;6] ekanligini topib oldik. Demak, to’plamning o’lchovi xossasidan Ratsional sonlarning o’lchovi nol ekanligidan uchbu to’plamlarning ayirmasini ham o’lchovi nolga teng. μ ( A / B )= 0 2-misol. E A  birlik kvadratdagi barcha ratsional koordinatali nuqtalar toplami bo‘lsin. A va A E \ to‘plamlar E da zich bo‘lganligi uchun 1=) \ ( 1,=) ( * * A E j A j tengliklar o‘rinli. Bu yerdan ). ( ) ( 0 =) ( * * * A j A j A j  va Demak, A to‘plam Jordan ma’nosida o‘lchovli emas. Ma’lumki, A - sanoqli to‘plam, shuning uchun uning elementlarini N k y x k k  ), , ( ko‘rinishda nomerlab chiqish mumkin. Shunday ekan }.,:),{(=, 1= kkkkkk k yyyxxxyxPPA    Ikkinchi tomondan ixtiyoriy N k uchun 0. =) ( kP m Bu yerdan 0 =) (* A  ekanligi kelib chiqadi. Shuni ta’kidlash kerakki, tashqi o‘lchovi nolga teng bo‘lgan har qanday to‘plam o‘lchovli to‘plamdir. Buning uchun elementar to‘plam sifatida Ø = B ni olish yetarli: . <0 =) ( =) Ø ( =) ( * * *     A A B A   28$ $Demak, A Lebeg ma’nosida o‘lchovli to‘plam. Shunday qilib, A Lebeg ma’nosida o‘lchovli bo‘lgan, lekin Jordan ma’nosida o‘lchovli bo‘lmagan to‘plamga misol bo‘ladi. 3 -misol. Kantor to‘plami K ning Lebeg o‘lchovi toping? Yechish. Kantor to‘plami K ning o‘lchovi 1=)\([0,1] K  tenglikdan kelib chiqadi. Barcha chiqarib tashlangan intervallar uzunliklari yig‘indisi   1.= 3 2 27 4 9 2 3 1 =) ( = 10 1 1= 1=                    n n n n n n K K K\], [    Demak, 0. =) (K  4-misol. 12=)( xxF funksiya yordamida qurilgan F Lebeg-Stiltes o‘lchovi absolyut uzluksiz o‘lchov bo‘ladi. Bu o‘lchov bo‘yicha (1;5]=A to‘plamning o‘lchovini toping. Yechish. Ta’rifga ko‘ra 8. = 3 11 = 1) 1 (2 1 5 2 = (1) (5) =) (        F F A F  5-misol. ] [ =) ( x x F funksiya yordamida qurilgan F Lebeg-Stiltes o‘lchovi diskret o‘lchov bo‘ladi. Chunki ] [ =) ( x x F funksiya monoton kamaymaydigan o‘ngdan uzluksiz funksiya bo‘lib, uning qiymatlar to‘plami butun sonlar to‘plami Z dan iborat. Butun sonlar to‘plami esa sanoqli to‘plamdir. Bu o‘lchov bo‘yicha {7;8} (1;5] =  A to‘plamning o‘lchovini toping. Yechish. Hosil qilingan F Lebeg-Stiltes o‘lchovi bo‘yicha ixtiyoriy Z n nuqtaning o‘lchovi birga teng. Chunki ] ; [ =} { n n n tenglik o‘rinli bo‘lgani uchun, ta’rifga ko‘ra   1.= 1) ( = 0) ( ) ( = ] ; [     n n n F n F n n F  29$

Demak, 2. = ({7;8}) F 
Endi (1;5]=B
to‘plamning o‘lchovini topamiz.
4. = 1 5 = (1) (5) =) (   F F B
F 
Berilgan
A to‘plam o‘zaro kesishmaydigan B va {7;8} to‘plamlarning
birlashmasidan iborat. O‘lchovning additivlik xossasiga ko‘ra
6. = 2 4 = ({7;8}) ) ( = ) (   F B F A
F 
XULOSA .
Mustaqil mamlakatimizning ijtimoiy-iqtisodiy, madaniy taraqqiyotida tub
o’zgarishlar qilish uning bosh maqsadidir. Kadrlar tayyorlash milliy dasturining
maqsadi – ta’lim sohasini tubdan isloh qilish, uni o’tmish dan qolgan mafkuraviy
qarashlar va sarqitlardan to’la xalos etish, rivojlangan demokratik davlatlar
darajasida, yuksak ma’naviy va axloqiy talablarga javob beruvchi yuqori malakali
kadrlar tayyorlash Milliy tizimini yaratishdir. Dunyoga yangi ko’z bilan
qaraydigan, uddaburon, ishning ko’zini biluvchi, buyuk kelajagimiz poydevorini
quruvchi va yuksaltiruvchi mutaxassis kadrlarni tayyorlash, respublikamiz
pedagoglari oldida turgan eng muhim va mashuliyatli vazifadir.
Men kurs ishimni yozishdan oldin to’plamdagi o’lchov tushunchani bilmasdim.
Shu kurs ishim orqali yangi bilimlarni o’rgandim. To’plamlarni o’lchovlarini
topishda mustaqil misollar ishlashni kurs ishimni yozish orqali mustahkamladim.
30

O’lchov tushunchasi juda ham keng tushuncha ekan. To’plamlar o’lchovi uning
xususiyat va elementlariga qarab o’zgarib borar ekan. Masalan, ratsional sonlar va
natural sonlar to’plamining o’lchovi nolga teng ekan. O’lchov tushunchasini
ko’plab olimlar fanga olib kirga. Biz asosan Jordan va Lebeg o’lchovlarini
o’rgandik. Ularrning xususiyatlari xar-hil ekan. O’lchov tushunchasi ko’plab
xossalarga ega ekan. To’plamning o’lchovi µ kabi belgilanadi.
Ushbu kurs ishi tayyorlash jarayonida dastlab shu mavzuga oid adabiyotlar,
manbalar tayyorladim. Tayyorlagan kurs ishi kirish, 4 ta paragrifdan iborat asosiy
qism, xulosa va foydalanilgan adabiyotlardan tashkil topgan. Lebeg ma’nosida
o’lchovli to’plamlar matematik analiz fanining eng asosiy va muhim bo’limlaridan
biri bo’lib, u xilma-xil tatbiqlarga ega. Shu sababdan, ushbu mavzu muhim va
asosiy ahamiyatga egadir. Garchi, bunday masala bilan “Matematik analiz” faning
umumiy kursida shug’ullanilsada, dasturda ko’zda tutilgan soatda uni atroflicha
o’rganish imkoniyati bo’ladi. Shu sababdan, mazkur masalani kurs ishining
mavzusi qilib tanlash bejiz emas. Bu masalani hal etish uchun dastlab mavzuga oid
qator adabiyotlarni to’plab, tegishli materiallarni tahlil etishga harakat qildim.
Ushbu kurs ishidan ana shunday maxsus hisoblash usullarini o`rganishda barcha
qiziquvchi talabalar foydalanishlari mumkin. Lebeg ma’nosida o’lchovli
to’plamlar mavzusi ustida bajariladigan misol va masalalar qiziqarli va
tushunarliligi bilan ajralib turar ekan. Ushbu mavzuda keltirilgan barcha misol va
masalalar talabalarni “Matematik analiz” faniga qiziqishini orttiradi.
Kurs ishidan Akademik litsey, kasb-hunar kollejlari va oliy ta’lim
muassasasi talabalari foydalanishlari mumkin.
31

FOYDALANILGAN ADABIYOTLAR .
1. О‘zbekiston Respublikasini yanada rivojlantirish bо‘yicha harakatlar
strategiyasi tо‘g‘risida O‘bekiston Respublikasi Prezidentining farmoni.
201 8 yil 8 fevraldagi 28 (6722)-soni.
2. Toshmetov O’., Turgunbayev R., Saydamatov E., Madirimov M. Matematik
analiz I-qism. T.: “Extremum-Press”, 2015. -390-398b.
3. Claudia Canuto, Anita Tabacco Mathematical analysis. I. Springer-Verlag.
Italia, Milan. 2008.- 331-338p.
4. Xudayberganov G., Vorisov A., Mansurov X., Shoimqulov B. Matematik
analizdan ma’ruzalar. I T.:«Voris-nashriyot». 2010 y. 288-293b.
5. Abdullaye J.I, G’anixo’jayev R.N, Shermatov .M.H. Haqiqiy
o’zgaruvchining funksiyalari nazariyasi. SamDu nashri, Toshkent-2009y.
97-118 b
6. S.Sarimsoqov, T.Toshpo’latov “Haqiqiy o’zgaruvchi funksiyalar
nazariyasi”. Toshkent-2007y
7. Internetdan:
W.W.W.google.uz,
W.W.W.ziyonet.uz,
W.W.W.referat.uz,
W.W.W.Yahoo.uz,
W.W.W. kitoblar.uz.
32

Oliy ta'lim muassalari asosiy fan uchun kerakli ma'lumot

Купить

Информация о документе

Продавец

Lebeg integrali

Похожие документы